39. 组合总和
39. 组合总和
DFS排列:每个元素可选0次,1次以及多次
public List<List<Integer>> combinationSum(int[] candidates, int target) {
//Arrays.sort(candidates);//注释了也能通过
this.candidates = candidates;
ans.clear();
comb(0,target,new ArrayList<Integer>());
return ans;
}
int[] candidates;
List<List<Integer>> ans = new ArrayList<>();
void comb(int k,int target,List<Integer> nums){
if(target==0){
ans.add(nums);
return;
}
// target后判断
if(k>=candidates.length) return;
//不选
comb(k+1,target,nums);
// 选一个或者多个
int t = target;
List<Integer> numst = new ArrayList<Integer>(nums);
while (t-candidates[k]>=0){
t -= candidates[k];// 本结点可以选多次
numst.add(candidates[k]);
comb(k+1,t,numst);
}
}
33. 搜索旋转排序数组
33. 搜索旋转排序数组
难点在于logN的时间复杂度
旋转之后的数据分为两个分别升序的部分,若能找到分割点(原来的a[0])那么在两部分分别进行两次二分查找,不就logN了
这个时候难点就在找分割点了,旋转次数是未知的,分割点也就未知,还得最高logN找分割点,这个时候题目转换成另外一个问题了。
153. 寻找旋转排序数组中的最小值
做完下面的153,再来做本题,就很简单了。
public int search(int[] nums, int target) {
int min = findMin(nums),low=0,high=nums.length-1;
if(target>nums[high]) high = min-1; //左边
else low = min;
// 接下来 low和high里二分查找即可
while (low<=high){//加等号 可能正好相遇时相等呢
int mid = (low+high)/2;
if(nums[mid]==target) return mid;
else if(nums[mid]<target) low = mid+1;
else high = mid-1;
}
return -1;
}
// 153. 寻找旋转排序数组中的最小值 改成返回最小值下标
public int findMin(int[] nums) {
int low=0,high=nums.length-1;
while (low<high){ // 区间长度为1时结束二分
int mid = (low+high)/2;
if(nums[mid]>nums[high]) low = mid+1; //改成+1 low右偏,一定在high相遇
else high = mid;
// 元素互不相同 不会出现相等的情况
}
return high;
}
接下来不找中点,直接用找中点 时nums[high]的性质,判断是在左半段还是右半段,其实用nums[0]也可以判断出来,就用nums[0]吧,target>nums[0] 一定左半段 target<nums[0] 一定在右半段,相等就直接找到了。 其实就是两个方法合二为一了
- 利用性质直接二分
还是二分,但是每次判断3点
- nums[mid]和target 谁大 taregt小,下标变化要舍弃nums里一些偏大的元素, 否则舍弃nums里比较小的元素
- target在左边还是右边 =》 根据target和nums[0]大小可以判断 这会影响舍弃元素时下标变化的策略
- mid 在左边还是右边 =》 根据mid 和nums[0]大小可以判断 这会影响舍弃元素时下标变化的策略
合起来一共23-2 = 6 种情况 。 舍弃的两种是:
- nums[mid]<target<nums[0] : 也就是不会出现 nums[mid]<target,target右边时(target<nums[0]) ,mid在左边(mid>nums[0])
- nums[mid]>target>nums[0] : 也就是不会出现 nums[mid]>target,target左边时(target>nums[0]) ,mid在右边(mid<nums[0])
153. 寻找旋转排序数组中的最小值
153. 寻找旋转排序数组中的最小值
不会,直接看题解,真的简单啊。简单分析一下,就会发现,
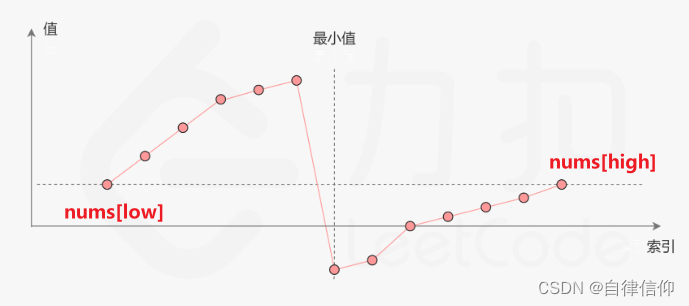
nums[high]有一个非常美的性质,取一个元素t, 若t<nums[high],一定在右半段,若t>nums[high],则一定在左半段。 中点 mid = (low+high)/2 ,中点值 nums[mid]必然也满足这个性质。
(“给你一个元素值 互不相同 的数组 nums” 数组元素互不相同)
mid在右半段,去掉其右边的:
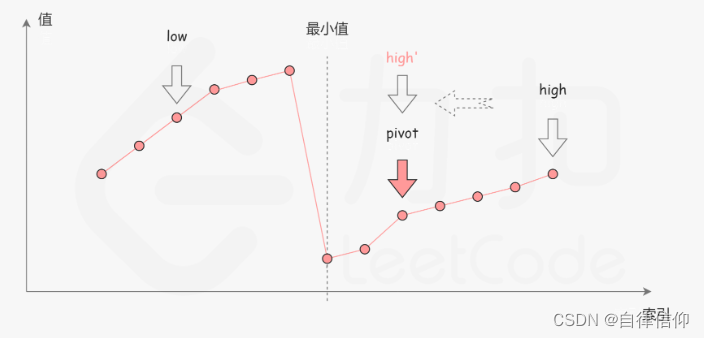
mid在左半段,去掉其左边的:
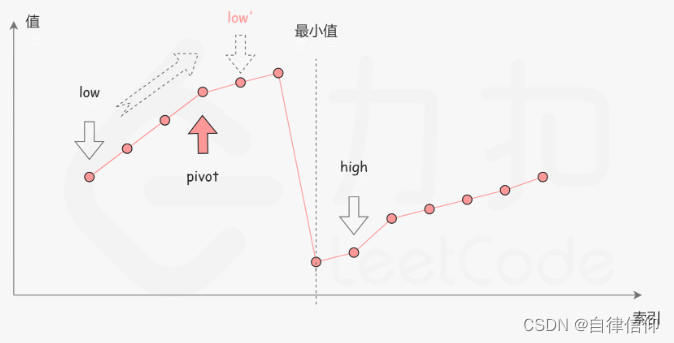
边界就自己举2个例子,一奇一偶,分别手算看看即可。初步分析,因为high在右边小的部分,
- 当然最简单的思路,最终只剩下两个元素时退出二分,取小的一个即可
public int findMin(int[] nums) {
int low=0,high=nums.length-1;
while (high-low>1){ // 区间长度为1时结束二分
int mid = (low+high)/2;
if(nums[mid]>nums[high]) low = mid;
else high = mid;
// 元素互不相同 不会出现相等的情况
}
return Math.min(nums[low],nums[high]); // 最后剩下两个 取一个最小的即可
}
真的要这么麻烦吗,为何要最后两个取最小,因为 mid = (low+high)/2 左偏了,最后一大一小时 会偏向小下标(大值)。而原本就有序时,左偏又是正确的。
那么让一大一小时,mid右偏不就行了,往右偏,最终相遇点一定偏小,(原本有序,肯定nums[0]相遇)
- mid = (low+high)/2+1 右偏即可
public int findMin(int[] nums) {
int low=0,high=nums.length-1;
while (low<high){ // 区间长度为1时结束二分
int mid = (low+high)/2;
if(nums[mid]>nums[high]) low = mid+1; //改成+1 low右偏,一定在high相遇
else high = mid;
// 元素互不相同 不会出现相等的情况
}
return nums[high];
}