简介
SRS(Simple Realtime Server)是一个简单高效的实时视频服务器,支持RTMP、WebRTC、HLS、HTTP-FLV、SRT等多种实时流媒体协议。
官网:https://ossrs.net/lts/zh-cn/

编译安装
使用ubuntu系统作为例子,最好是20版本。
1、克隆项目代码
git clone -b 4.0release https://gitee.com/ossrs/srs.git
上面是克隆4.0分支,也可以克隆所有版本的。
2、配置、编译
cd srs/trunk
./configure
make
应用
1、启动服务
./objs/srs -c conf/srs.conf
编译后可执行文件在objs/目录下;
延迟问题:
配置文件在conf/下,SRS的 低延迟配置为 conf/realtime.con,如果延迟太高,SRS 启动的时候使用低延迟配置。命令如下:
./objs/srs -c ./conf/realtime.conf
2、判断SRS是否成功启动
有三种方法
(1)打开 http://localhost:8080/
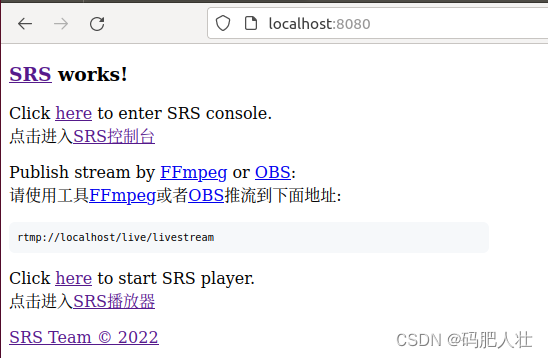
(2)查看SRS的状态
命令:
./etc/init.d/srs status
输出:
MB0:trunk $ ./etc/init.d/srs status
SRS(pid 90408) is running. [ OK ]
(3)或者看SRS的日志
命令:
tail -n 30 -f ./objs/srs.log
输出:
MB0:trunk $ tail -n 30 -f ./objs/srs.log
[2021-08-13 10:30:36.634][Trace][90408][12c97232] Hybrid cpu=0.00%,0MB, cid=1,1, timer=61,0,0, clock=0,22,25,0,0,0,0,1,0
3、推流、拉流
这里不细讲,测试的时候可以使用obs推流,使用VLC拉流(串流)。
4、关闭服务
(1)查找文件对应的pid。
pgrep -f ./objs/srs
(2)杀死进程
kill 25958