LeetCode：455. 分发饼干——贪心算法

news2024/10/6 10:41:45

🍎道阻且长，行则将至。🍓

🌻算法，不如说它是一种思考方式🍀

算法专栏： 👉🏻123

贪心算法是在每个阶段选取局部最优解，最终得到全局最优解的一种思想。贪心算法与动态规划的思路相似，但贪心算法要在每个阶段选择最优解，而这个最优解不一定是全局最优解，贪心算法在某些情况并不能得到全局最优解。

贪心算法的基本思路：

找到最优子结构：将问题分解为多个子问题，并且每个子问题具有最优子结构，即解决子问题的最优解可以组合成原问题的最优解。
找到贪心策略：为了解决每个子问题，找出一种最优策略，使得每个子问题都采用该策略，最终可以得到原问题的最优解。
证明贪心策略的合理性：贪心策略在每个阶段选取局部最优解，最终可以得到全局最优解。

一、🌱455. 分发饼干

题目描述：假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。
对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。
来源：力扣（LeetCode）
难度：简单
提示：
1 <= g.length <= 3 * 10⁴
0 <= s.length <= 3 * 10⁴
1 <= g[i], s[j] <= 2³¹ - 1
示例 1:
输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。所以你应该输出1。
示例 2:
输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出2。

🌴解题

我们可以很容易想到，优先把小的饼干给胃口小的孩子吃，或者先把大的饼干给胃口大的孩子。这其实就是一种贪心策略。
因此我们先需要对两个数组进行排序，然后依次遍历饼干或者胃口数组，找出满足的值。
例如
对于孩子胃口数组：
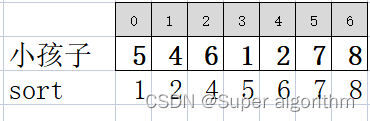
在这里插入图片描述
饼干尺寸数组：

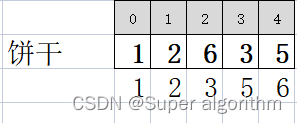
以i遍历小孩子胃口数组，用index指向饼干，那么按小饼干先分配，则i和index都是从0开始：

贪心

code：

class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int num=0,index=0;
        for (int i = 0; i < s.length&&index<g.length; i++) {
            if(s[i]>=g[index]) {
                num++;
                index++;
            }
        }
        return num;

    }
}