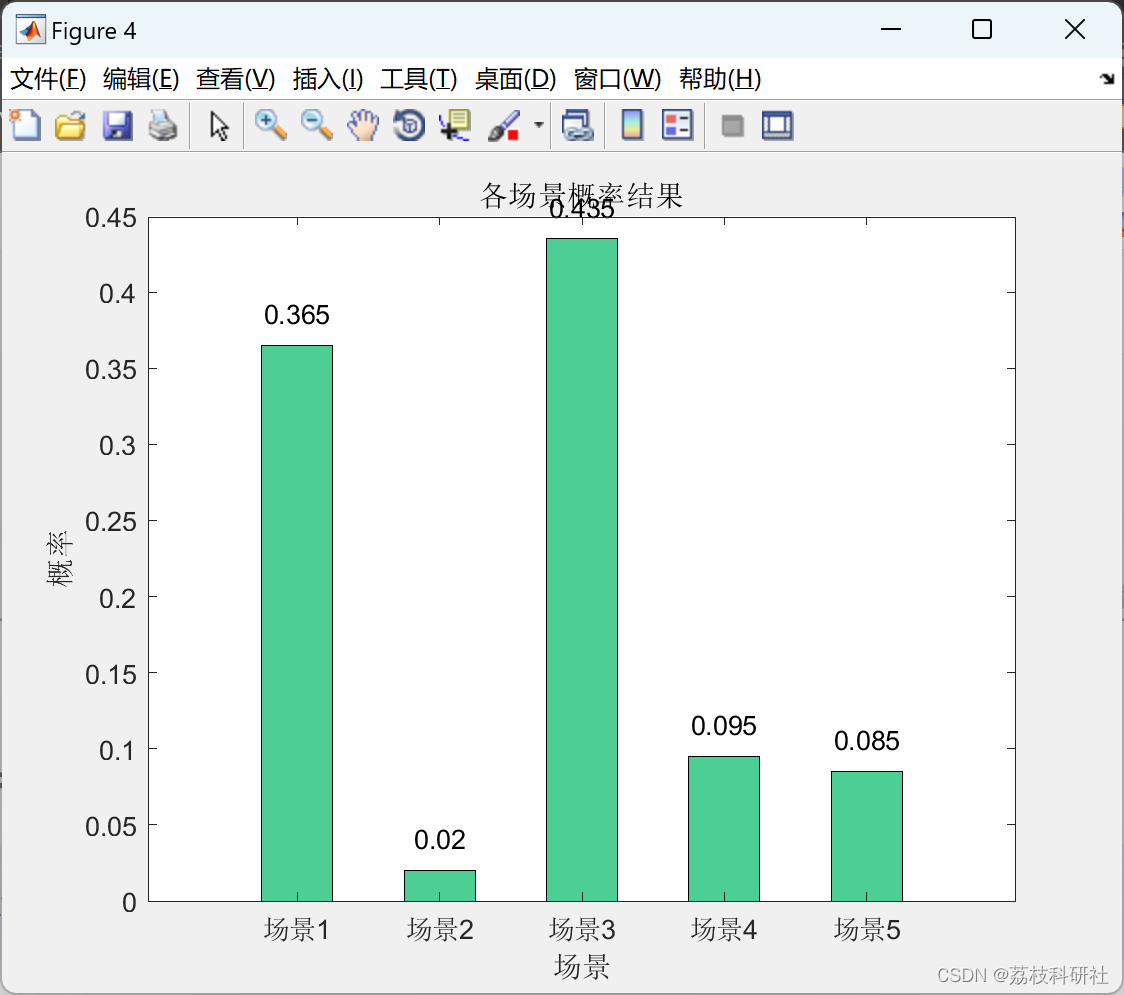
491.递增子序列

思路：

1.确定回溯函数参数：定义全局遍历存放res集合和单个path，还需要

nums数组
startindex（int）为下一层for循环搜索的起始位置。

2.终止条件：当startindex >len(nums)，return；如果len(path) >= 2，则将当前递增子序列添加到 res 数组中（注意：不用返回，因为还要继续向下查找）

3.遍历过程：去重，for循环层（树层）不能使用相同元素

判断nums[i]在本层是否出现过，出现过跳出
判断是否递增，非递增跳出
若不跳出：记录nums[i],加入path，继续遍历，回溯

class Solution:
    def findSubsequences(self, nums: List[int]) -> List[List[int]]:
        res = []
        path = []
        def backtrack(nums,startindex):
            if startindex>len(nums):
                return
            if len(path)<=len(nums) and len(path) >= 2:
                res.append(path[:])
            nums_dict = set()
            for i in range(startindex,len(nums)):
                if path and path[-1]>nums[i] or nums[i] in nums_dict:
                    continue
                nums_dict.add(nums[i])
                path.append(nums[i])
                backtrack(nums,i+1)
                path.pop()
        backtrack(nums,0)
        return res

46.全排列

思路：

首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。

1.确定回溯函数参数：定义全局遍历存放res集合和单个path，还需要

nums数组

2.终止条件：当len(path)==len(nums)时，将当前结果放入res

3.遍历过程：去重，for循环层（树层）不能使用相同元素

判断nums[i]在本层是否出现过，出现过跳出
判断是否递增，非递增跳出
若不跳出：记录nums[i],加入path，继续遍历，回溯

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        res = []
        path = []
        def backtrack(nums):
            if len(path)==len(nums):
                res.append(path[:])
                return
            for i in range(len(nums)):      #枚举可选择元素
                if nums[i] in path:         #选取不在当前路劲元素
                    continue
                path.append(nums[i])        #选择元素
                backtrack(nums)             #递归搜索
                path.pop()                  #撤销选择
        backtrack(nums)
        return res

47.全排列 II

思路：

重复数字数组，去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了

1.确定回溯函数参数：定义全局遍历存放res集合和单个path，还需要

nums数组
check数组，记录此时path里都有哪些元素使用了，一个排列里一个元素只能使用一次

2.终止条件：当len(path)==len(nums)时，将当前结果放入res

3.遍历过程：去重，for循环层（树层）不能使用相同元素

判断nums[i]是否使用过，if check[i] ==1
判断前一个相同元素是否使用过，if i > 0 and nums[i] == nums[i-1] and check[i-1] == 0:
若不跳出：check[i]=1，选择元素，递归，回溯，check[i]=0

1. if i > 0 and nums[i] == nums[i-1] and check[i-1] == 0

灰色为剪枝部分，蓝色为答案部分：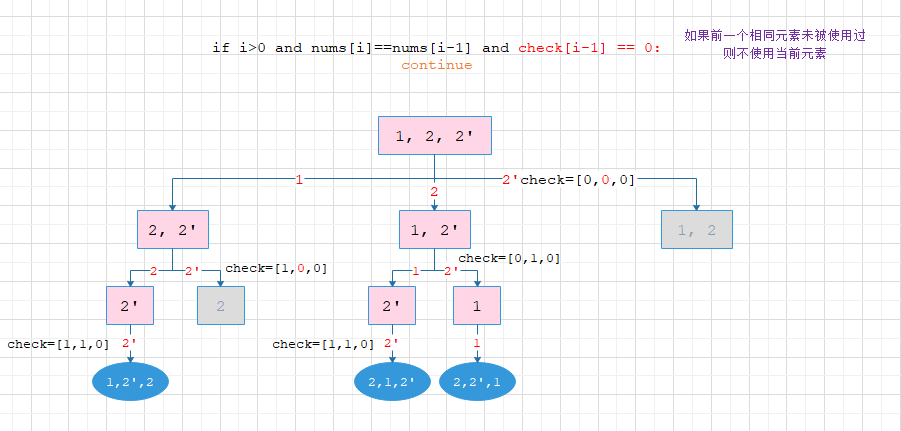

2. if i > 0 and nums[i] == nums[i-1] and check[i-1] == 1

灰色为剪枝部分，蓝色为答案部分：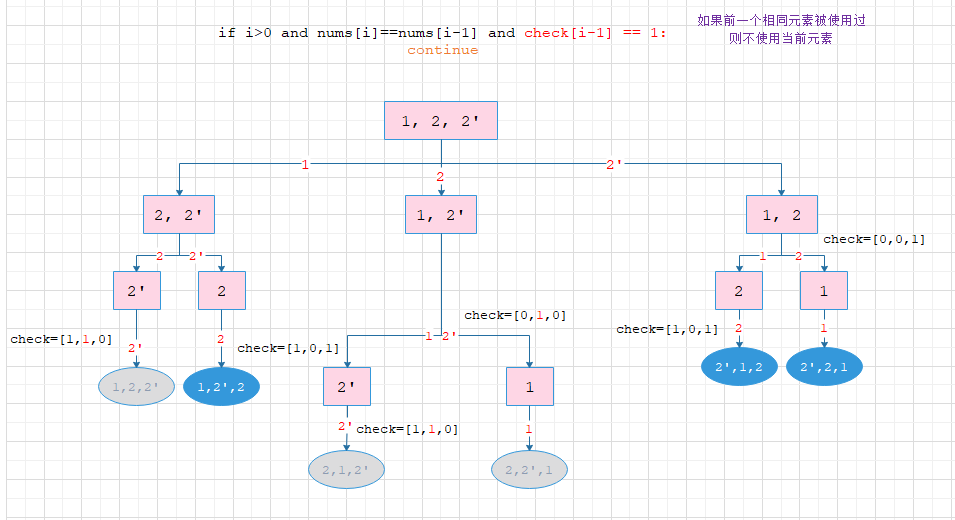

能够明显发现第一种能够提前剪枝，减少计算步骤和搜索次数，并且第一种选择了重复元素的第一个，而第二种选择了重复元素的最后一个

参考链接：47. 全排列 II - 力扣（Leetcode）题解

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        res = []
        path = []
        nums.sort()
        check = [0 for i in range(len(nums))]
        def backtrack(nums,check):
            if len(path)==len(nums):
                res.append(path[:])
                return
            for i in range(len(nums)):      
                if check[i] == 1:
                    continue
                if i > 0 and nums[i]==nums[i-1] and check[i-1] == 0:
                    continue
                check[i] = 1
                path.append(nums[i])        #选择元素
                backtrack(nums,check)       #递归搜索
                path.pop()                  #撤销选择
                check[i] = 0
        backtrack(nums,check)
        return res