前言

本周阅读文献《Improving LSTM hydrological modeling with spatiotemporal deep learning and multi-task learning: A case study of three mountainous areas on the Tibetan Plateau》，文章主要基于时空深度学习（DL）即将二维卷积神经网络（CNN）和LSTM耦合的水文模型，并在实际案例中测试所提出的模型，和LSTM模型及进行对比，发现所提出的模型在性能方面会好一些，此外通过使用LR模型进一步探讨CNN和LSTM模型的物理可解释性，以研究CNN和LSTM可能捕获的潜在水文和气象信息。另外，主要学习了时序预测的传统时间序列预测，总结了常用的11中传统时序预测的方法，总结了三个主要模型的优缺点。

This week,I read an article which proposes a spatiotemporal deep-learning (DL)-based hydrological model that couples the 2-Dimension convolutional neural network (CNN) and LSTM.The proposed CNN-LSTM model is tested on three large mountainous basins on the Tibetan Plateau, and the results are compared to those obtained from the LSTM-only model.And this paper explores the physical interpretability of CNN and LSTM models by using the LR model to look into potential hydrological and meteorological information CNN and LSTM may capture.In addition,I mainly learn the traditional time series prediction. And I summarize the 11 commonly traditional time series prediction methods,the advantages and disadvantages of three models.

文献阅读

题目：Improving LSTM hydrological modeling with spatiotemporal deep learning and multi-task learning: A case study of three mountainous areas on the Tibetan Plateau
作者：Bu Li a, , , , , , Ruidong Li aTing Sun bAofan Gong aFuqiang Tian aMohd Yawar Ali Khan cGuangheng Ni a

摘要

长短期记忆（LSTM）网络已经证明了其在处理长时间序列方面的出色能力，并已被证明在降水径流建模中是有效的。然而，目前的LSTM水文模型缺乏多任务学习和空间信息的结合，限制了其充分利用气象和水文数据的能力。为了解决这个问题，本研究提出了一种基于时空深度学习（DL）的水文模型，该模型将二维卷积神经网络（CNN）和LSTM耦合，并引入实际蒸发（Ea）作为额外的训练目标。在青藏高原的三个大山盆地上测试了所提出的CNN-LSTM模型，并将结果与仅LSTM模型的结果进行了比较。此外，还使用probe方法探索所提出的深度学习模型的内部嵌入层。结果表明，LSTM和CNN-LSTM水文模型在模拟径流（Q）和Ea方面表现良好，具有（NSEs）分别高于 0.82 和 0.95。较高NSEs建议将空间信息引入仅 LSTM 模型可以提高整体模型和峰值模型性能。总体而言，本研究证明了空间信息和多任务学习在LSTM水文建模中的价值，并为解释DL模型的内部嵌入层提供了视角。

简介

水文模型，无论是基于物理的还是数据驱动的，在洪水和干旱灾害预防以及水资源管理中发挥着至关重要的作用。数据驱动的模型可以直接描述输入和输出之间的统计关系，而无需明确描述物理过程。

当前基于 DL 的水文模型在水文建模方面很有前途，但在三个值得注意的方面仍需要改进：
(1)解析时空特征的能力：水文过程建模在很大程度上取决于气象强迫的空间模式和底层表面特征。Yang等人（2020）利用计算机视觉来解决ANN P-Q建模中的空间特征，并证明空间信息在增强模型鲁棒性方面起着重要作用。然而，大多数关于 LSTM 水文建模的现有研究几乎利用流域空间平均气象数据作为模型输入（例如，Jiang 等人，2022 年，Kratzert 等人，2018 年，Lees 等人，2021 年），而没有完全表示 LSTM 水文建模输入的空间特征。耦合2-D CNN和LSTM有望通过同时考虑时间动力学和空间特征来弥合这种差距（Miao等人，2019，Shi等人，2015），CNN-LSTM已被证明在不同领域很有前途（例如，临近预报（苗等人，2019 年，Shi 等人，2015 年）和水质预测（Barzegar 等人，2020 年，杨等人，2021 年））。

(2)考虑多个水文过程：与基于物理的水文模型不同，基于LSTM的模型模拟单个水文过程，例如(Feng 等人，2020 年，Frame 等人，2021 年）、地下水（Ali 等人，2022 年，Nourani 等人，2022 年）和雪水当量（段和乌尔里希，2021 年），但很少同时模拟多个过程。这使得基于 LSTM 的水文模型难以明确考虑不同水文过程之间的相互作用，也难以诊断基于水文理论（例如水平衡方程）的模型（Reichstein 等人，2019 年）。此外，一些研究发现，引入额外的水文过程，例如实际蒸发（表示为Ea在这项工作中）过程中，在基于物理的水文模型的校准中可以增强模拟性能（赫尔曼等人，2018 年，内斯鲁等人，2020 年）。因此，研究基于LSTM的水文模型同时考虑多个水文过程是否可以提高其描绘更多水文过程的能力，从而提供更全面的水文变量诊断，这是有益的。

(3)物理可解释性：由于“黑匣子”性质，基于 DL 的水文模型没有明确表示物理过程，因此仍然受到一些水文学家的质疑（Nearing 等人，2021 年）。为了增强用户和政策制定者对采用基于深度学习的水文模型的信心，最近有人试图提高对其物理可解释性的理解（Arrieta 等人，2020 年，Jiang 等人，2022 年）。例如，LSTM水文模型已被证明可以学习基础物理过程的可推广表示。LSTM 区域水文模型优于区域校准的 DHM，甚至针对每个盆地单独校准（Feng 等人，2020 年，Kratzert 等人，2019 年，Sun 等人，2021 年）。此外，发现 LSTM 水文模型能够存储与水文知识一致的隐藏信息（Jiang 等人，2022 年，Kratzert 等人，2018 年，Lees 等人，2022 年）。然而，深度学习模型的物理可解释性相对于过程Ea - 水文循环中的关键组成部分 - 还有待研究。此外，CNN-LSTM模型中CNN输出的物理概念仍不清楚。

方法

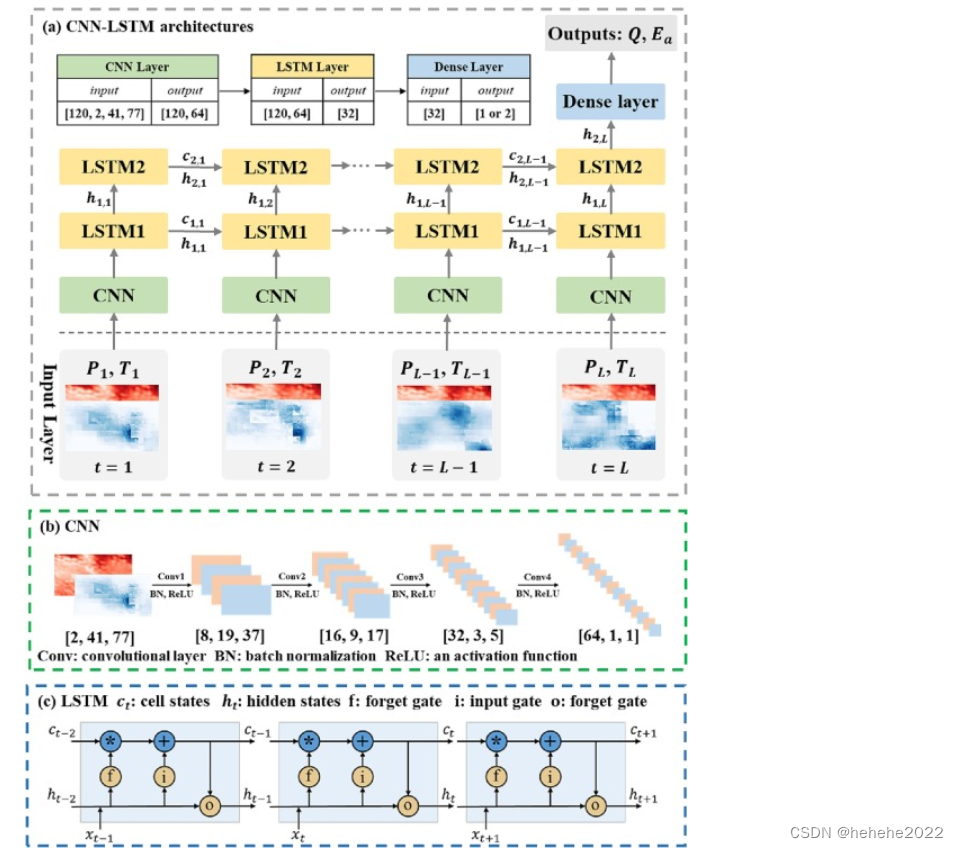
提出了一种基于深度学习的水文模型，通过耦合2-D CNN和LSTM来利用它们各自的优势：前者用于分层空间特征提取，而后者用于学习长时间依赖性。该模型可以使用二维空间气象和底层地表数据作为输入，并预测每日水文过程Q和Ea作为输出。注意到每天只有气象数据P和T平均温度作为输入，该模型可以通过设置训练目标来执行单任务或多任务学习：前者模拟单个水文过程，而后者同时关注两个或多个过程。
模型图，如图：
在这里插入图片描述
卷积神经网络（CNN）
CNN是一种特殊类型的前馈神经网络，包括输入层、卷积层、池化层和全连接层（LeCun et al.， 1998）。卷积层是 CNN 的核心，它使用卷积核从各种 N 维模型输入中提取信息。我们利用二维CNN来捕获气象数据的空间信息。卷积层通过减小输入（特征）的空间大小（宽度和高度）、增加通道数并最终生成一维序列来处理气象数据。

长短期记忆（LSTM）网络
LSTM 模型旨在缓解RNN 在处理长时间序列方面的弱点。LSTM的成功在于记忆细胞（细胞状态）和隐藏单元格（隐藏状态）中，分别捕获缓慢和快速演化过程的内部架构。此外，设计了三个门（即输入、忘记和输出）来分别控制每个单元格中要存储、删除和传递的信息。这些架构有利于 LSTM 模型处理长时间动态。

多任务学习
多任务（MT）学习是在基于DL的模型中将多个任务设置为优化目标（Caruana，1997）。培训可以从MT信息的丰富表示中受益，从而使用其他任务中的信息来提高每个任务的性能。此外，与单任务（ST）学习相比，机器翻译学习可以实现更高的效率和更少的过度拟合，因为它可以将模型引导到多个相关任务首选的更通用的特征表示（Li 等人，2023 年）。
物理可解释性方法
DL 水文模型的内部嵌入层包含大量无法明确解释的数据。这些数据可能隐藏了一些未经训练的内部水文变量。本研究利用探针回归模型将训练模型的内部嵌入层映射到未经训练的水文变量来测试经过训练的 DL 模型是否可以学习已知但未经训练的水文变量，并检查模型的内部表示和进一步的物理可解释性。最简单的probe形式是线性回归（LR）模型，它将学习的嵌入层连接到给定的输出。

CNN-LSTM 模型的性能
CNN-LSTM模型在所有三个研究盆地中都非常有效NSEs大于0.89，并能以适当的幅度和时机准确捕捉Q的峰值。将结果与其他相关研究中的一些传统水文模型进行比较，结果表明CNN-LSTM模型优于它们。

结论

本研究通过耦合CNN和LSTM，开发了一种基于时空dl的水文模拟集成模型，并在黄河、长江和澜沧江的水源地进行了评估。此外，我们采用简单的线性回归方法探索CNN和LSTM在基于DL的水文模型中的物理可解释性，以提高我们对DLM推断的水文过程的理解。

时间序列预测

传统的时间序列预测
传统的时间序列预测方法主要是针对具体数据，设计数学（形态函数）模型，捕捉时序特征规律完成预测工作。其预测的针对性强，鲁棒性好，可解释，但是学习自由度低，泛化性差。
常见的时间序列预测方法：
1、指数平滑Exponential Smoothing
2、Holt-Winters 法
3、自回归 (AR)
4、移动平均模型(MA)
5、自回归滑动平均模型 (ARMA)
6、差分整合移动平均自回归模型 (ARIMA)
7、季节性 ARIMA (SARIMA)
8、包含外生变量的SARIMA (SARIMAX)
9、向量自回归 (VAR)
10、向量自回归滑动平均模型 (VARMA)
11、包含外生变量的向量自回归滑动平均模型 (VARMAX)
下面对这几种方法进行具体的介绍：
1.使用平滑技术进行时间序列预测
指数平滑Exponential Smoothing
在做时序预测时，一个显然的思路是：认为离着预测点越近的点，作用越大。比如我这个月体重100斤，去年某个月120斤，显然对于预测下个月体重而言，这个月的数据影响力更大些。假设随着时间变化权重以指数方式下降——最近为0.8，然后0.82，0.83…，最终年代久远的数据权重将接近于0。将权重按照指数级进行衰减，这就是指数平滑法的基本思想。

指数平滑法是过去观测值的加权平均值，随着观测值变老，权重呈指数会衰减。换句话说，观察时间越近相关权重就越高。它可以快速生成可靠的预测，并且适用于广泛的时间序列。
指数平滑法有几种不同形式：一次指数平滑法针对没有趋势和季节性的序列，二次指数平滑法针对有趋势但没有季节性的序列，三次指数平滑法针对有趋势也有季节性的序列。“Holt-Winters”有时特指三次指数平滑法。

一次指数平滑法：此方法适用于预测没有明确趋势或季节性模式的单变量时间序列数据。简单指数平滑法将下一个时间步建模为先前时间步的观测值的指数加权线性函数。
它需要一个称为 alpha (a) 的参数，也称为平滑因子或平滑系数，它控制先前时间步长的观测值的影响呈指数衰减的速率，即控制权重减小的速率。a 通常设置为 0 和 1 之间的值。较大的值意味着模型主要关注最近的过去观察，而较小的值意味着在进行预测时会考虑更多的历史。简单指数平滑时间序列的简单数学解释如下所示：
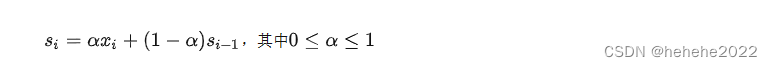
在这里插入图片描述
si是时间步长i（理解为第i个时间点）上经过平滑后的值，xi是这个时间步长上的实际数据。

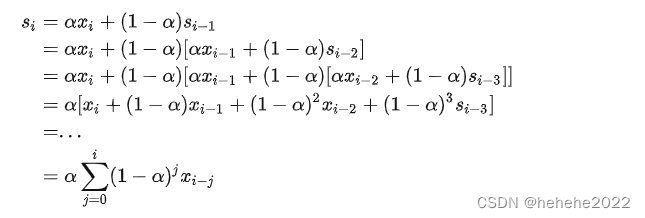
可以看出，在指数平滑法中，所有先前的观测值都对当前的平滑值产生了影响，但它们所起的作用随着参数alpha 的幂的增大而逐渐减小。一次指数平滑所得的计算结果可以在数据集及范围之外进行扩展，因此也就可以用来进行预测。预测方式为：
在这里插入图片描述
si是最后一个已经算出来的值。h等于1代表预测的下一个值。

二次指数平滑法:
趋势也就是我们所说的斜率，b=Δy/Δx，除了用点的增长量表示，也可以用二者的比值表示趋势。比如可以说一个物品比另一个贵20块钱，等价地也可以说贵了5%，前者称为可加的（addtive），后者称为可乘的（multiplicative）。
指数平滑考虑的是数据的baseline，二次指数平滑在此基础上将趋势作为一个额外考量，保留了趋势的详细信息。即我们保留并更新两个量的状态：平滑后的信号和平滑后的趋势。公式如下：
在这里插入图片描述第二个等式描述了平滑后的趋势。当前趋势的未平滑“值”（ti）是当前平滑值（si）和上一个平滑值（Si-1）的差；也就是说，当前趋势告诉我们在上一个时间步长里平滑信号改变了多少。要想使趋势平滑，我们用一次指数平滑法对趋势进行处理，并使用参数β（理解：对 ti的处理类似于一次平滑指数法中的si,即对趋势也需要做一个平滑，临近的趋势权重大）
为获得平滑信号，我们像上次那样进行一次混合，但要同时考虑到上一个平滑信号及趋势。假设单个步长时间内保持着上一个趋势，那么第一个等式的最后那项就可以对当前平滑信号进行估计。

若要利用该计算结果进行预测，就取最后那个平滑值，然后每增加一个时间步长就在该平滑值上增加一次最后那个平滑趋势：
在这里插入图片描述

三次指数平滑法 Holt-Winters 法
在 1957 年初，Holt扩展了简单的指数平滑法，使它可以预测具有趋势的数据。这种被称为 Holt 线性趋势的方法包括一个预测方程和两个平滑方程（一个用于水平，一个用于趋势）以及相应的平滑参数 α 和 β。后来为了避免趋势模式无限重复，引入了阻尼趋势法，当需要预测许多序列时，它被证明是非常成功和最受欢迎的单个方法。除了两个平滑参数之外，它还包括一个称为阻尼参数 φ 的附加参数。
一旦能够捕捉到趋势，Holt-Winters 法扩展了传统的Holt法来捕捉季节性。Holt-Winters 的季节性方法包括预测方程和三个平滑方程——一个用于水平，一个用于趋势，一个用于季节性分量，并具有相应的平滑参数 α、β 和 γ。

此方法有两种变体，它们在季节性成分的性质上有所不同。当季节变化在整个系列中大致恒定时，首选加法方法，而当季节变化与系列水平成比例变化时，首选乘法方法。
当一个序列在每个固定的时间间隔中都出现某种重复的模式，就称之具有季节性特征，而这样的一个时间间隔称为一个季节(理解：比如说在一个周内，销量呈现出重复的模式)。一个季节的长度k为它所包含的序列点个数。

二次指数平滑考虑了序列的baseline和趋势，三次就是在此基础上增加了一个季节分量。类似于趋势分量，对季节分量也要做指数平滑。比如预测下一个季节第3个点的季节分量时，需要指数平滑地考虑当前季节第3个点的季节分量、上个季节第3个点的季节分量…等等。详细的有下述公式(累加法)：
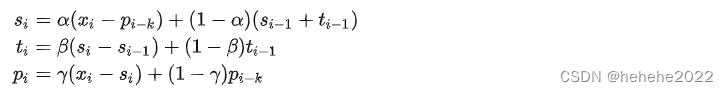
在这里插入图片描述
其中， pi 是指“周期性”部分。预测公式如下：

k是这个周期的长度。
2.单变量时间序列预测
自回归 (AR)
自回归模型描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测。
在 AR 模型中，我们使用变量过去值的线性组合来预测感兴趣的变量。术语自回归表明它是变量对自身的回归。
一般的P阶自回归模型 AR：
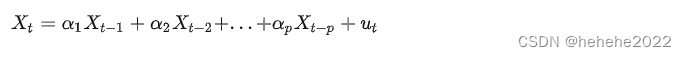
在这里插入图片描述

自回归模型有很多的限制：
（1）自回归模型是用自身的数据进行预测
（2）时间序列数据必须具有平稳性
（3）自回归只适用于预测与自身前期相关的现象（时间序列的自相关性）

移动平均模型 (MA)
与在回归中使用预测变量的过去值的 AR 模型不同，MA 模型在类似回归的模型中关注过去的预测误差或残差。
在AR模型中，如果 ut 不是一个白噪声，通常认为它是一个q阶的移动平均。即
在这里插入图片描述
需要指出一点，AR模型中历史白噪声的影响是间接影响当前预测值的（通过影响历史时序值）。

自回归滑动平均模型 (ARMA)
在 AR 模型中，我们使用变量过去值与过去预测误差或残差的线性组合来预测感兴趣的变量。它结合了自回归 (AR) 和移动平均 (MA) 模型。
AR 部分涉及对变量自身的滞后（即过去）值进行回归。MA部分涉及将误差项建模为在过去不同时间同时发生的误差项的线性组合。模型的符号涉及将 AR§ 和 MA(q) 模型的顺序指定为 ARMA 函数的参数，例如 ARMA（p，q）。
将AR（p）与MA（q）结合，得到一个一般的自回归移动平均模型ARMA（p，q）：
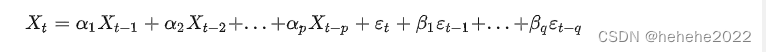
在这里插入图片描述
表明：
（1）一个随机时间序列可以通过一个自回归移动平均模型来表示，即该序列可以由其自身的过去或滞后值以及随机扰动项来解释。

（2）如果该序列是平稳的，即它的行为并不会随着时间的推移而变化，那么我们就可以通过该序列过去的行为来预测未来。

差分整合移动平均自回归模型 (ARIMA)
如果我们将差分与自回归和移动平均模型相结合，我们将获得 ARIMA 模型。ARIMA 是差分整合移动平均自回归模型Autoregressive Integrated Moving Average model 的首字母缩写。它结合了自回归 (AR) 和移动平均模型 (MA) 以及为了使序列平稳而对序列的差分预处理过程，这个过程称为积分(I)，得到了差分自回归移动平均模型 ARIMA（p、d、q），其中 d 是需要对数据进行差分的阶数。

ARMA模型可以说是平稳时间序列建模中很常用的方法了，但是局限性也很明显—“平稳”。

一般生活中的数据很难满足平稳性要求，比较常用的转化为平稳序列的做法就是差分，一阶差分不行二阶差分，几次差分后终能平稳，所以ARIMA(p,d,q)在ARMA(p,q)的基础上把差分的过程包含了进来，多了一步差分过程，对应就多了一个参数d，也因此ARIMA可以处理非平稳时间序列。

因此ARIMA有一个不足之处，就是不能很好的处理周期型序列。虽说也可以用差分方式平稳化，但需要的是k步差分（季节差分，x = diff(x, k)）。所以说ARIMA对周期型序列来说还有不足。

季节性 ARIMA (SARIMA)
SARIMA（Seasonal ARIMA）：ARIMA的扩展版本，可以支持带有季节性成分的时间序列数据。在ARIMA(p,d,q)基础上又增加了3个超参数(P,D,Q)，以及一个额外的季节性周期参数 s。

SARIMA(p,d,q)(P,D,Q,s)总共7个参数，可以分成2类，3个非季节参数(p,d,q)，和4个季节参数(P,D,Q,s)。

3.外生变量的时间序列预测
包含外生变量的SARIMAX (SARIMAX)
SARIMAX 模型是传统 SARIMA 模型的扩展，包括外生变量的建模，是Seasonal Autoregressive Integrated Moving-Average with Exogenous Regressors 的缩写
外生变量是其值在模型之外确定并施加在模型上的变量。它们也被称为协变量。外生变量的观测值在每个时间步直接包含在模型中，并且与主要内生序列的使用不同的建模方式。
SARIMAX 方法也可用于通过包含外生变量来模拟具有外生变量的其他变化，例如 ARX、MAX、ARMAX 和 ARIMAX。

具有外生回归量的向量自回归移动平均 (VARMAX)
Vector Autoregression Moving-Average with Exogenous Regressors (VARMAX) 是 VARMA 模型的扩展，模型中还包含使用外生变量的建模。它是 ARMAX 方法对多个并行时间序列的推广，即 ARMAX 方法的多变量版本。
VARMAX 方法也可用于对包含外生变量的包含模型进行建模，例如 VARX 和 VMAX。

4.多元时间序列预测
向量自回归 (VAR)
向量自回归模型（vector autoregressive model，简称VAR模型）是非结构性方程组模型，由Sims于1980年提出。该模型不以经济理论为基础，采用多方程联立的形式，在模型的每一个方程中，内生变量对模型的全部内生自变量的滞后项进行回归，进而估计全部内生变量的动态关系，常用于预测相互联系的时间序列系统以及分析随机扰动对变量系统的动态冲击。
VAR 模型是单变量自回归模型的推广，用于预测时间序列向量或多个并行时间序列，例如多元时间序列。它是关于系统中每个变量的一个方程。
如果序列是平稳的，可以通过将 VAR 直接拟合到数据来预测它们（称为“VAR in levels”）。如果序列是非平稳的，我们会取数据的差异以使其平稳，然后拟合 VAR 模型（称为“VAR in differences”）。
我们将其称为 VAR§ 模型，即 p 阶向量自回归模型。

向量自回归移动平均 (VARMA)
VARMA 方法是 ARMA 对多个并行时间序列的推广，例如多元时间序列。具有有限阶 MA 误差项的有限阶 VAR 过程称为 VARMA。
模型的公式将 AR§ 和 MA(q) 模型的阶数指定为 VARMA 函数的参数，例如 VARMA（p，q）。VARMA 模型也可用于VAR 或 VMA 模型。

总结

指数平滑法：
优点：数据需求量小，只需少量数据即可对未来需求进行预测，简单易行。
缺点：难以找到最佳的指数值（a等），无法对需求的突变进行预测，对需求变化调整缓慢。
适用于短期预测，更长远的预测效果差。
自回归AR：
优点：简单，仅用自身变量数列就可以进行预测。
缺点：变量必须具有自相关，只适用于预测与自身前期相关的经济现象，对社会影响较大的社会现象，不宜采用自回归。
arima：
优点：模型简单，只需要内生变量而不需要借助其他外生变量。
缺点：要求时序数据是稳定的或者通过差分后是稳定的，本质上只能捕捉线性关系，不能捕捉非线性关系。

文献：
Applications of deep learning in water quality management: A state-of-the-art review
文献主要概述了DL在WQ水质管理中的应用，涵盖了2011年至2022年的发展，简要介绍了深度学习模型的不同变体，包括循环神经网络（RNN）、长短期记忆网络（LSTM）、卷积神经网络（CNN）等，讨论DL模型在河流、湖泊、沿海地区等各种水体中预测WQ参数的应用。