122.买卖股票的最佳时机II
贪心算法
思路:
把利润分解为每天为单位的维度,而不是从0天到第3天整体去考虑!
那么根据prices可以得到每天的利润序列:(prices[i] - prices[i - 1])…(prices[1] - prices[0])。
如图:
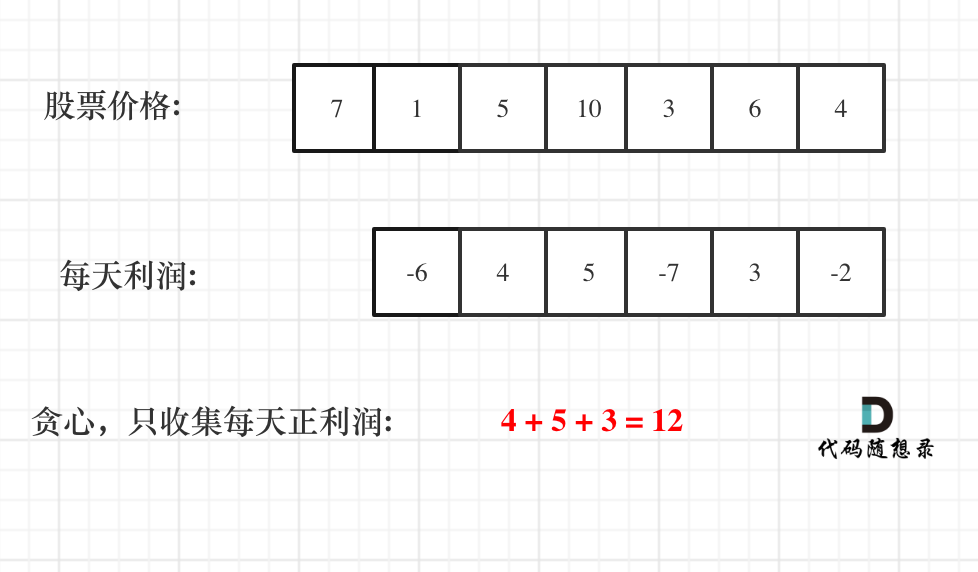
从图中可以发现,其实我们需要收集每天的正利润就可以,收集正利润的区间,就是股票买卖的区间,而我们只需要关注最终利润,不需要记录区间。
那么只收集正利润就是贪心所贪的地方!
局部最优:收集每天的正利润,全局最优:求得最大利润。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
res = 0
for i in range(1,len(prices)):
res += max(0,prices[i]-prices[i-1])
return res
动态规划
- 状态定义
状态表示:
状态方程
=
{
d
p
[
i
]
[
0
]
=
表示第
i
天交易完后,手上没有股票时的最大利润,
d
p
[
i
]
[
1
]
=
表示第
i
天交易完后,手上持有股票时的最大利润。
状态方程 = \begin{cases} dp[i][0] =表示第 i 天交易完后,手上 没有 股票时的最大利润,\\ dp[i][1] =表示第 i 天交易完后,手上 持有 股票时的最大利润。 \end{cases}
状态方程={dp[i][0]=表示第i天交易完后,手上没有股票时的最大利润,dp[i][1]=表示第i天交易完后,手上持有股票时的最大利润。
- 状态转移
状态转移方程为:
{ d p [ i ] [ 0 ] = m a x ( d p [ i − 1 ] [ 0 ] , d p [ i − 1 ] [ 1 ] + p r i c e s [ i ] ) d p [ i ] [ 1 ] = m a x ( d p [ i − 1 ] [ 1 ] , d p [ i − 1 ] [ 0 ] − p r i c e s [ i ] ) \begin{cases} dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i]) \\ dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i]) \end{cases} {dp[i][0]=max(dp[i−1][0],dp[i−1][1]+prices[i])dp[i][1]=max(dp[i−1][1],dp[i−1][0]−prices[i])
- 初始化
对第一天(i=0)的状态进行初始化:
dp[0] [0]: 第一天手上无股票,也没有购入股票。
dp[0] [1]: 第一天手上持有股票说明在当天购入了股票,花费 prices[0]prices[0]prices[0],即所获利润为 −prices[0]-prices[0]−prices[0]。
- 执行结果
遍历全部的日期i,则最后一天手上没有股票时的状态值dp[n-1] [0]即为我们能够获得的最大利润。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
# dp[i][0]:第i天结束后,手上没有股票的最大利润(第i天卖出股票 )
# dp[i][1]:第i天结束后,手术持有股票的最大利润(第i天买入股票)
dp = [[0]*2 for _ in range(n)]
# 初始化
dp[0][0] = 0
dp[0][1] = -prices[0]
for i in range(1,n):
# dp[i][0]:max(前一天没有股票,前一天持有股票+当天卖出)
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+prices[i])
# dp[i][1]:max(前一天持有股票,前一天没有股票+当天买入)
dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i])
return max(dp[n-1][0],dp[n-1][1])
# return dp[n - 1][0]
55.跳跃游戏
思路:
其实跳几步无所谓,关键在于可跳的覆盖范围!
不一定非要明确一次究竟跳几步,每次取最大的跳跃步数,这个就是可以跳跃的覆盖范围。
这个范围内,别管是怎么跳的,反正一定可以跳过来。
那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点!
每次移动取最大跳跃步数(得到最大的覆盖范围),每移动一个单位,就更新最大覆盖范围。
贪心算法局部最优解:每次取最大跳跃步数(取最大覆盖范围),整体最优解:最后得到整体最大覆盖范围,看是否能到终点。
具体步骤:
- 初始化能到达的最远位置max_i为 0。
- 遍历数组 nums。
- 如果能到达当前位置,即 max_i<i,并且当前位置 + 当前位置最大跳跃长度 > 能到达的最远位置,即 i + nums[i] > max_i,则更新max_i。
- 遍历完数组,最后比较能到达的最远位置 max_i和数组最远距离 size - 1 的关系
class Solution:
def canJump(self, nums: List[int]) -> bool:
size = len(nums)
max_i = 0
for i in range(size-1):
if max_i >=i and i + nums[i] > max_i:
max_i = i + nums[i]
return max_i >= size -1
45.跳跃游戏II
真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最小步数!
需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖。
思路:
- 当前所能达到的最远位置 end,下一步所能跳到的最远位置 max_pos,最少跳跃次数 setps
- 遍历数组 nums 的前 len(nums) - 1个元素:
- 每次更新第 i位置下一步所能跳到的最远位置 max_pos
- 如果索引 i到达了 end 边界,则:更新 end为新的当前位置 max_pos,并令步数steps+1
- 最终返回跳跃次数 steps。
class Solution:
def jump(self, nums: List[int]) -> int:
end = 0
max_pos = 0
step = 0
for i in range(len(nums)-1):
max_pos = max(i + nums[i],max_pos)
if i == end:
end = max_pos
step += 1
return step





![[学习笔记]计算机图形学(一)](https://img-blog.csdnimg.cn/img_convert/1460cdbf0d4754eca14b73389e9564c9.png)