【数据结构】堆（笔记总结）

news2024/10/7 8:23:51

在这里插入图片描述

👦个人主页：@Weraphael
✍🏻作者简介：目前学习C++和算法
✈️专栏：数据结构
🐋 希望大家多多支持，咱一起进步！😁
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 📂 加关注✨

【本章内容】
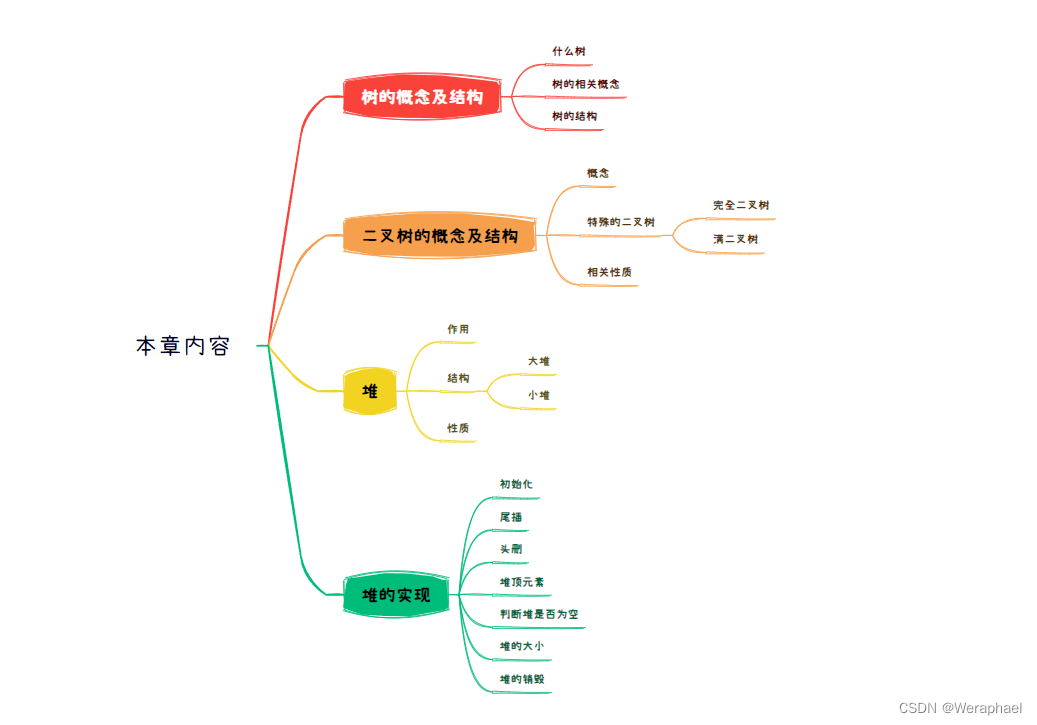
在这里插入图片描述

目录

  • 一、树的概念及结构
      • 1.1 什么是树
      • 1.2 树的相关概念（常见）
      • 1.3 树的结构
  • 二、二叉树的概念及结构
      • 2.1 概念
      • 2.2 特殊的二叉树
      • 2.3 二叉树的性质
  • 三、堆
      • 3.1 二叉树的顺序结构
      • 3.2 堆的性质
      • 3.3 堆的结构
      • 3.4 堆的作用及父子关系
  • 四、堆的实现
      • 4.1 准备工作
      • 4.2 常见接口
      • 4.3 堆的初始化
      • 4.4 堆的尾插
      • 4.5 堆的头删
      • 4.6 堆顶元素
      • 4.7 判断堆顶是否为空
      • 4.8 堆的大小
      • 4.9 堆的销毁

一、树的概念及结构

1.1 什么是树

树是一种非线性的数据结构，它是由n(n ≥ 0)个有限结点组成的一个具有层次关系的集合，把它叫做树是因为它看起来像一颗倒挂的树，也就是说，二叉树是根朝上，而叶是朝下的。

如上图所示，树可以分成根和子树。举个例子，A是根，则BEFJ、CGKL、DHI就是子树；接下来B也能称为根，则EFJ就是他的子树，后面以此类推，因此树是递归定义的

  • 注意：树形结构中，子树之间不能有交集，否则就不是树形结构

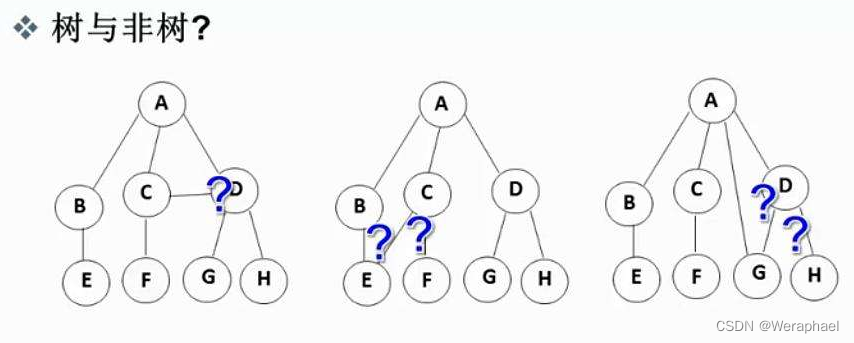
在这里插入图片描述

以上三种皆不是树形结构。那什么样的才算是树呢？

  1. 子树是不相交的。
  2. 除了根结点外，每个结点有且仅有一个父结点。
  3. 一颗N个结点的树有N-1条边。

1.2 树的相关概念（常见）

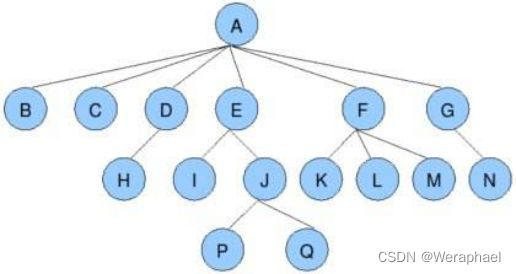
在这里插入图片描述

  1. 结点的度：一个结点含有的子树的个数称为该结点的度（根的孩子的个数）。如上图，A作为根，其结点的度为6.
  2. 叶子结点：度为0的结点（无孩子的）。如上图，B、C、H、I、P、Q、K、L、M、N都是叶结点
  3. 父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点； 如上图：A是B的父结点
  4. 孩子结点：一个结点含有的子树的根结点称为该结点的子结点； 如上图：B是A的孩子结点
  5. 树的高度（深度）：树中结点的最大层次； 如上图：树的高度为4
  6. 结点的祖先：从根到该结点所经分支上的所有结点；如上图：A是所有结点的祖先
  7. 子孙：以某结点为根的子树中任一结点都称为该结点的子孙。如上图：所有结点都是A的子孙

1.3 树的结构

左孩子有兄弟表示法

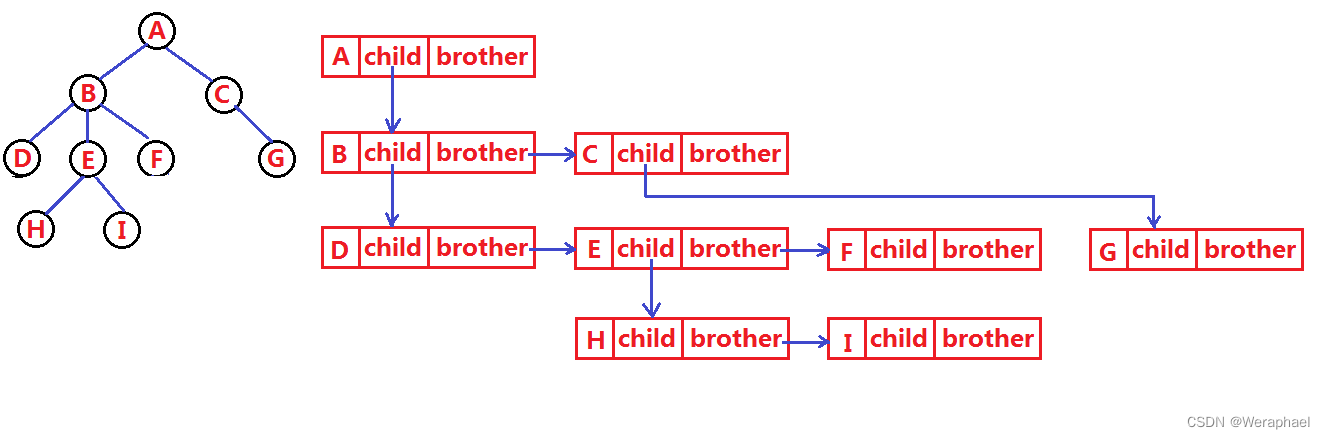
在这里插入图片描述

typedef int DataType;
struct Node
{
	struct Node* LeftChild1;  // 左孩子结点
	struct Node* Brother; // 兄弟结点
	DataType data; // 结点中的数据
};

二、二叉树的概念及结构

2.1 概念

一颗二叉树是结点的一个有限集合，该集合：

  1. 可能为空。
  2. 或者由一个根结点加上两颗别称为左子树和右子树组成。

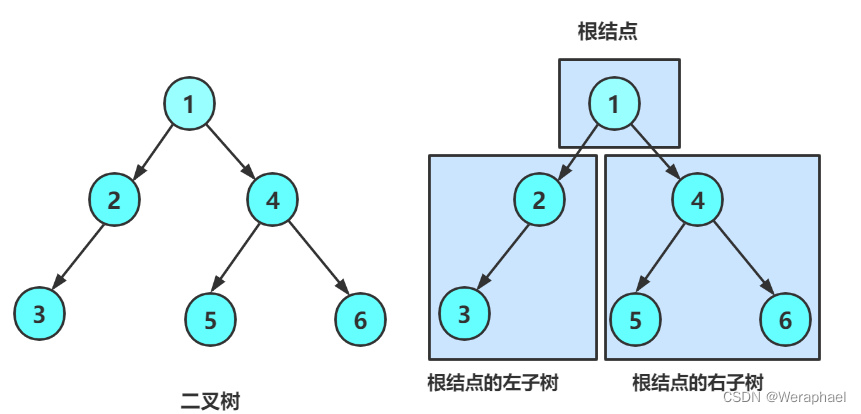
在这里插入图片描述

从上图可以看出：

  1. 二叉树不存在度大于2的结点，也就是说，二叉树的根的孩子不能超过2个（计划生育的树hh）
  2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

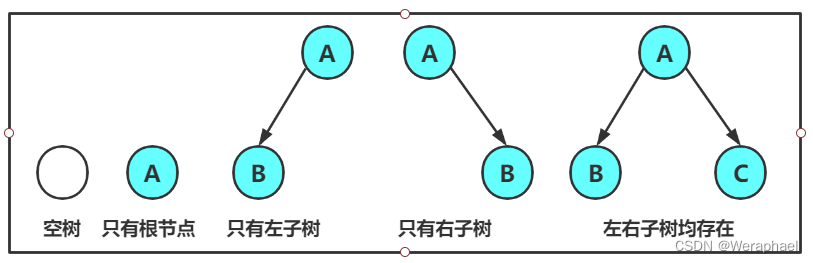
注意：对于任意的二叉树都是由以下5种情况复合而成的：
在这里插入图片描述

2.2 特殊的二叉树

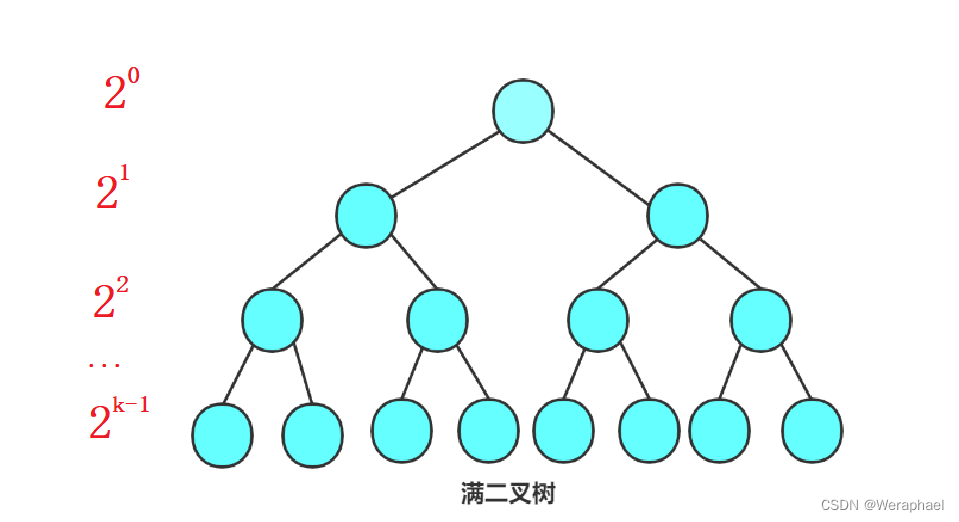
  • 满二叉树：如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。

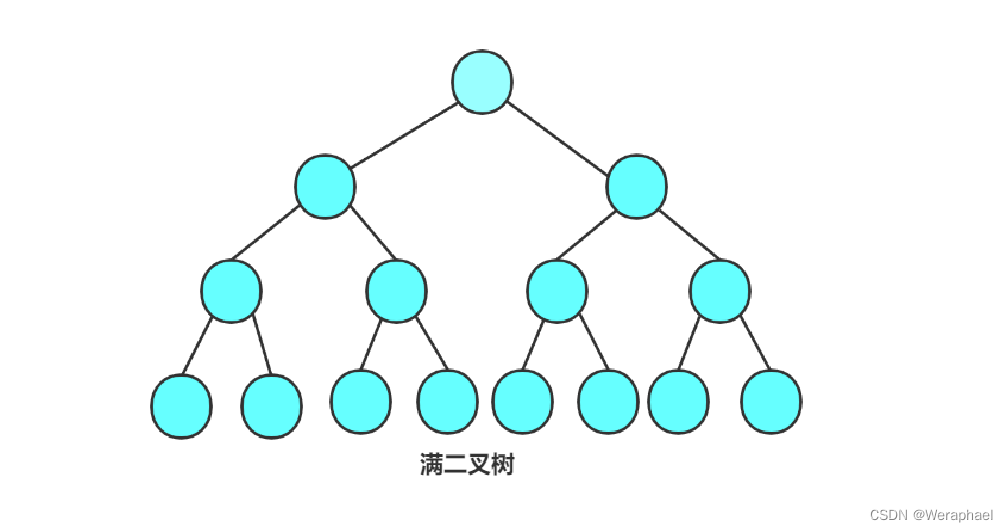
在这里插入图片描述

那么接下来问题来了，如果说一个二叉树的高度为K，如何推算出满二叉树的结点总数呢？
在这里插入图片描述
从上图中，对每一层的个数分析，发现这就是一个等比数列，因此，可以利用等比数列求和公式来算出结点总数，满二叉树结点总数为：2n - 1

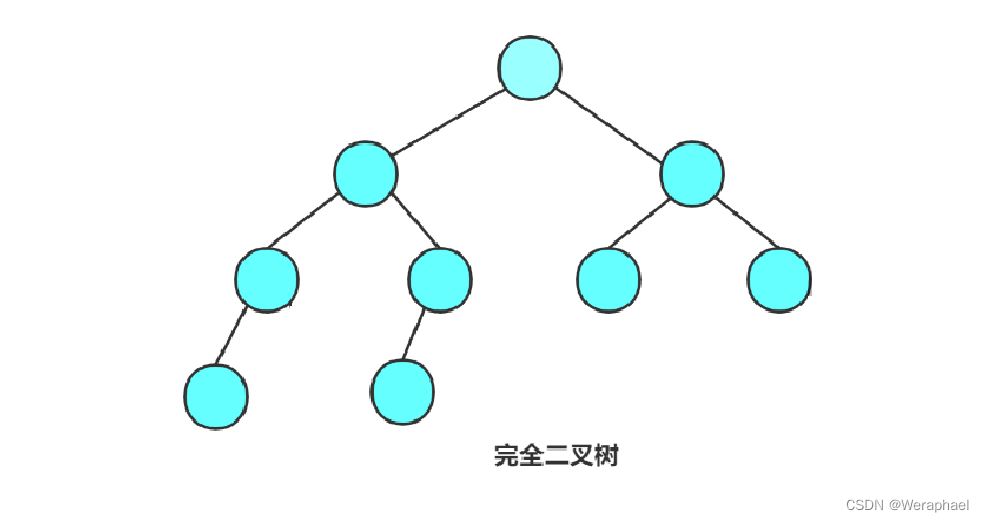
  • 完全二叉树：完全二叉树是效率很高的数据结构。它是由满二叉树而引出来的。

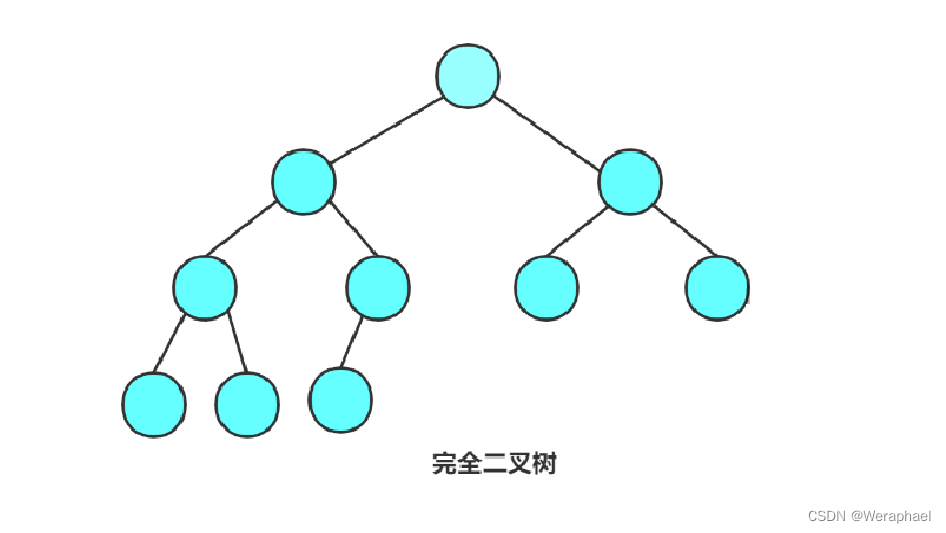
在这里插入图片描述

完全二叉树结构特点：

  1. 假设有k层，前k-1层是满的
  2. 最后一层要求从左到右是要连续的

问：下面是否是完全二叉树？
在这里插入图片描述
答案：不是，因为它的最后一层不连续。

最后一个问题，如果说一个二叉树的高度为K，求完全二叉树结点总数的范围？
答案：[2k-1，2k - 1]

解析：
首先，满二叉树是一种特殊的完全二叉树，所以结点个数最多的情况就是满二叉树，因此个数为2k - 1
最后，最小的极限情况就是当完全二叉树最后一层只有一个结点的时候。因此，可以先计算前k - 1层的结点总数，根据等比数列求出个数为：2k-1 - 1，然后再加上最后一层的最后一个节点，因此，结果就为：2k-1
【例题】
一颗完全二叉树的结点个数 为531个，那么这棵树的高度为多少？B
A 11
B 10
C 8
D 12
做法：将ABCD代入[2k-1，2k - 1]，若531在其范围内，则就是答案。

2.3 二叉树的性质

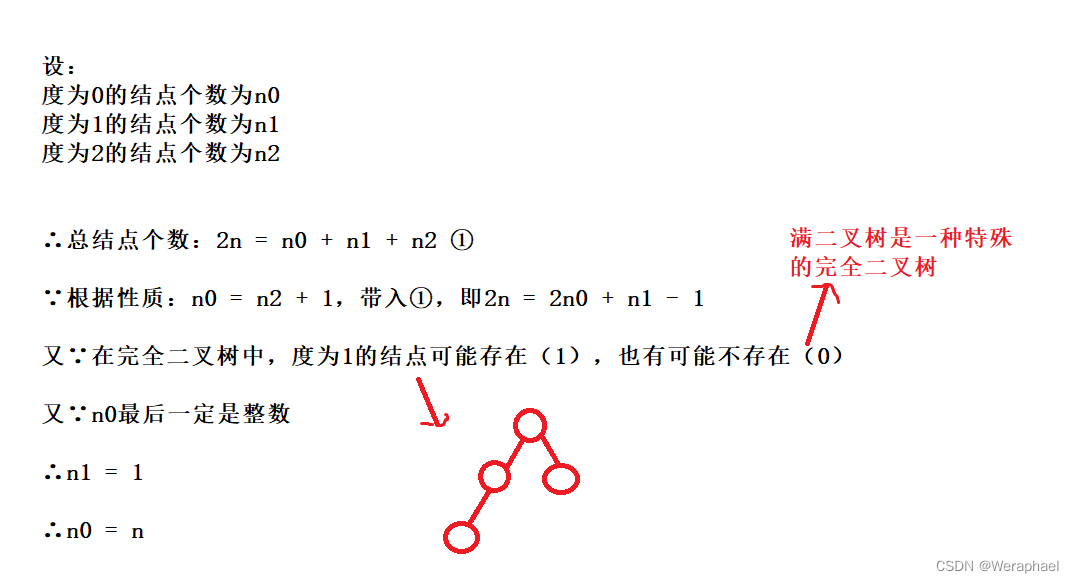
对任何一颗二叉树，如果度为0（叶结点）的结点个数为n0，度为2的结点个数为n2，则有n0 = n2 + 1（度为0的永远比度为2的多一个）
【证明】
在这里插入图片描述

【例题1】
某二叉树共有399个结点，其中有199个度为2的结点，则该二叉树中的 叶节点个数为多少？
答案 ： 200
解析：
首先叶结点就是度为0的结点，然后根据性质：n0 = n2 + 1，即可得出叶结点的个数为200

【例题2】
在具有2n个结点的完全二叉树中，叶结点的个数为多少？
在这里插入图片描述

三、堆

3.1 二叉树的顺序结构

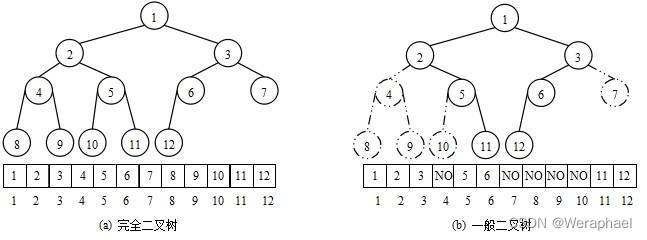
  1. 普通的二叉树是不适合用数组来存储的，因为它会存在空间浪费的情况（如下图）
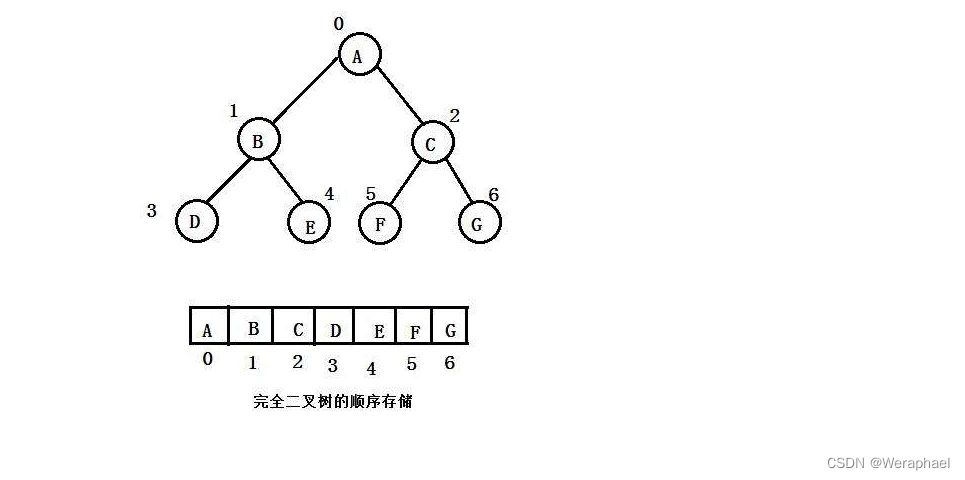
    在这里插入图片描述

  2. 从物理的角度看（实实在在在内存中的存储）：二叉树顺序存储是一个数组；从逻辑的角度看（想象出来的）：它是一个二叉树 （如上图a）

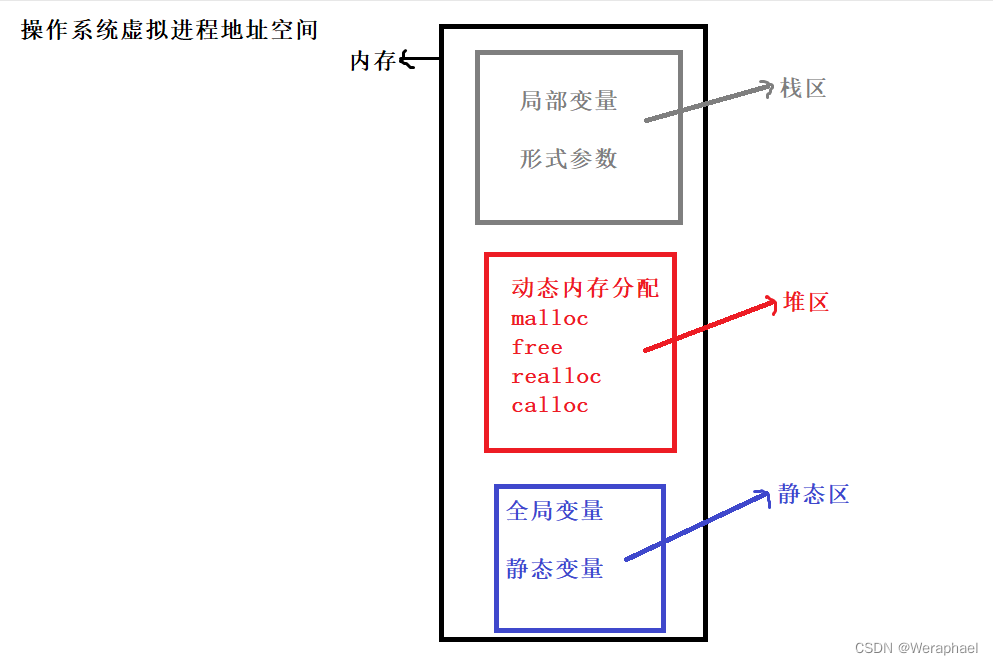
  3. 我们通常把堆（一种二叉树）使用顺序结构的数据来存储。需要注意的是，这里的堆和操作系统虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。
    在这里插入图片描述

3.2 堆的性质

我们通常把堆（一种二叉树）使用顺序结构的数据来存储，但是存储并没有什么意义，因此引入了堆的性质（结构）

  • 堆的性质：
  1. 堆中某个节点的值总是不大于或不小于其父节点的值
  2. 堆总是一棵完全二叉树

3.3 堆的结构

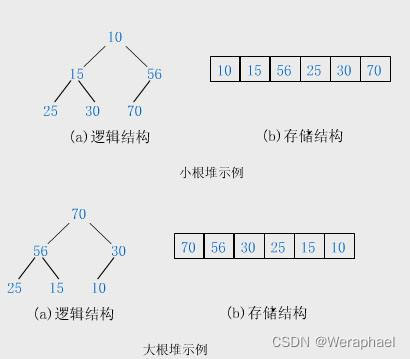
  • 小根堆又称小堆，其特点是：父亲结点总小于或等于孩子结点
  • 大根堆又称大堆：其特点是：父亲结点总大于或等于孩子结点
    在这里插入图片描述

3.4 堆的作用及父子关系

在实现堆之前，先说明堆的作用及父子关系

  • 堆的作用

常用来频繁变动的数据集中找出最值。 比如，小堆的根结点是整个二叉树中最小的，大堆的根结点是整个二叉树最大的。还能找到次大（次小）的，只要删除堆顶元素，再重新建堆，即可实现。

  • 父子关系

在这里插入图片描述
通过下标关系，不难可以写出以下关系

  1. 如何找到父亲结点：parent = （child - 1）/ 2
  2. 如何找到左孩子结点 ：leftchild = parent * 2 + 1
  3. 如何找到右孩子结点：rightchild = parent * 2 + 2（右孩子比左孩子的下标多1）

四、堆的实现

4.1 准备工作

为了方便管理，我们可以创建多个文件来实现
test.c - 测试代码逻辑 （源文件）
heap.c - 动态的实现 （源文件）
heap.h - 存放函数的声明 （头文件）
在这里插入图片描述【工具：visual studio】

4.2 常见接口

【heap.h】

typedef int hptypedata;

typedef struct heap
{
	hptypedata* a;
	int size;
	int capacity;
}hp;


//结构体初始化
void HeapInit(hp* hph);

//尾插
void HeapPush(hp* hph, hptypedata x);

//头删
void HeapPop(hp* hph);

//堆顶元素
hptypedata HeapTop(hp* hph);

//判断堆是否为空
bool HeapEmpty(hp* hph);

//堆的个数大小
int HeapSize(hp* hph);

//堆的销毁
void HeapDestroy(hp* hph);

void HeapPush(hp* hph, hptypedata x);

//向上调整
void AdjustUp(hptypedata* a, int child);

//向下调整
void AdjustDown(hptypedata* a, int parent);

4.3 堆的初始化

【heap.c】

void HeapInit(hp* hph)
{
	assert(hph);

	hph->a = (hptypedata*)malloc(sizeof(hptypedata) * 4);
	if (hph->a == NULL)
	{
		perror("hph->a :: malloc");
		return;
	}
	hph->capacity = 4;
	hph->size = 0;
}

其实就是顺序表的初始化，详情 —>[传送门]

4.4 堆的尾插

void Swap(hptypedata* p1, hptypedata* p2)
{
	hptypedata tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustUp(hptypedata* a, int child)
{
	//找到父亲节点
	int parent = (child - 1) / 2;

	while (child > 0) //while (parent >= 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			//交换完迭代继续
			child = parent;
			parent = (child - 1) / 2;
		}
		//如果尾插的节点不比其父亲大，就没必要比了
		else
		{
			break;
		}
	}
}

void HeapPush(hp* hph, hptypedata x)
{
	assert(hph);

	// 可能会扩容
	if (hph->size == hph->capacity)
	{
		hptypedata* tmp = (hptypedata*)realloc(hph->a, sizeof(hptypedata) * hph->capacity * 2);
		if (tmp == NULL)
		{
			perror("tmp :: realloc");
			return;
		}
		hph->a = tmp;
		hph->capacity *= 2;
	}
	//插入
	hph->a[hph->size] = x;
	hph->size++;
	
	//向上调整
	AdjustUp(hph->a, hph->size - 1);
	//hph->size - 1 指的是尾插元素（孩子）的下标
}

【笔记总结】

以上代码以大堆为例

  1. 首先尾插后，由于还要保持大堆的性质，如果尾插的结点要比其父结点大，就要进行向上调整
    【动图展示】
    在这里插入图片描述
  2. 为什么多了一个交换函数Swap?
    因为后面一些接口也会交换两个数，为了让代码复用，因此写了一个Swap函数
  3. 在向上调整中，不用while (parent >= 0)的原因
    首先这个循环条件也是可以正常运行的。但是，当parent迭代指向根节点(下标0)，此时执行了if语句，child就迭代到根节点，其parent = (0 - 1) / 2 = 0，循环结束后parent等于0还是会进入循环，而此时parent和child同时在根节点，虽然不会死循环，但是有点多次一举，就像庄周带净化
  4. 向上调整有一个前提：除了child这个位置，前面的数据必须保持堆的性质

4.5 堆的头删

void AdjustDown(hptypedata* a, int n,int parent)
{
	//假设左孩子一开始最大
	int child = parent * 2 + 1;
	//当child走到叶子节点循环结束，也就是说它不能超过数组的大小
	while (child < n)
	{
		//判断右孩子是否真的比左孩子大
		//注意还要防止数组越界
		if (child + 1 < n && a[child + 1] > a[child])
		{
			child++;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			//迭代
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapPop(hp* php)
{
	assert(php);
	//空的顺序表不能删
	assert(!HeapEmpty(php));

	//不能挪动数据删，一方面效率低下，另一方面父子关系会乱
	//正确方法：交换头尾，再进行尾删
	
	//交换
	Swap(&php->a[0], &php->a[php->size - 1]);
	//尾删
	php->size--;

	//保证是大堆性质，进行向下调整
	AdjustDown(php->a, php->size,0);
}

【笔记总结】

  1. 为什么堆有头删却没有尾删？
    首先堆的尾删是没有意义的，即使删了尾，它还是个堆。
    而头删是有意义的，当它和heaptop接口配合起来。当它是大堆时，就能选出第一大、第二大…小堆也是如此
  2. 头删为什么不能直接删头？
    第一点：顺序表头删效率低
    第二点：即使头删会导致关系混乱
    正确做法：先头尾交换，再删掉尾（间接把头删了），最后再进行向下调整
  3. 在向下调整的过程中，由于要满足大堆的性质，当前的根结点要与自己的两个孩子比较大小，大的那个作为新的根。那么如何优雅的比较呢？首先可以利用假设逻辑，假设一开始左孩子最大，然后再判断是否左孩子真的大于右孩子，如果右孩子真的大于左孩子，则让child++，因为左孩子和右孩子的下标关系相差1
  4. 向下调整的前提是：左右子树都要保持大堆或者小堆的性质

【动图展示】
在这里插入图片描述

4.6 堆顶元素

hptypedata HeapTop(hp* php)
{
	assert(php);
	return php->a[0];
}

下标为0的元素即是堆顶元素

4.7 判断堆顶是否为空


bool HeapEmpty(hp* hph)
{
	assert(hph);

	return hph->size == 0;
}

4.8 堆的大小

int HeapSize(hp* hph)
{
	assert(hph);

	return hph->size;
}

4.9 堆的销毁

void HeapDestroy(hp* hph)
{
	assert(hph);

	free(hph->a);
	hph->a = NULL;
	hph->size = 0;
	hph->capacity = 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/416055.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MySQL--数据库基础--0406

MySQL--数据库基础--0406

目录 1.什么是数据库&#xff1f; 2. 基本使用 2.1 连接服务器 2.2 数据库的操作在Linux中的体现 2.3 使用案例 3.服务器&#xff0c;数据库&#xff0c;表关系 4.数据逻辑存储 5.SQL的分类 6.存储引擎 1.什么是数据库&#xff1f; 数据库和文件 文件或者数据库&…
阅读更多...
OK-MX93开发板-实现Web页面无线点灯

OK-MX93开发板-实现Web页面无线点灯

上篇文章&#xff1a;i.MX9352——介绍一款多核异构开发板&#xff0c;介绍了OK-MX9352开发板的基础硬件功能。 本篇来使用OK-MX9352开发板&#xff0c;通过Web界面进行点灯测试&#xff0c;最终的效果如下&#xff1a; 在进行代码编写之前&#xff0c;先在Ubuntu虚拟机上把这…
阅读更多...
对比损失Contrastive Loss（CVPR 2006）原理解析

对比损失Contrastive Loss（CVPR 2006）原理解析

paper&#xff1a;http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf 本文提出的对比损失contrastive loss被广泛应用于自监督模型中&#xff0c;但最初对比损失是作为一个特征降维方法而提出的。 摘要 降维是学习一种映射关系&#xff0c;通过这种映射关…
阅读更多...
day10 线程池及gdb调试多线程

day10 线程池及gdb调试多线程

目录 线程池的概念 概念&#xff1a; 必要性&#xff1a; 线程池的基本结构&#xff1a; 线程池的实现 完整代码 线程的GDB调试 线程池的概念 概念&#xff1a; 通俗的讲就是一个线程的池子&#xff0c;可以循环的完成任务的一组线程集合&#xff1b; 必要性&#xff…
阅读更多...
【软件工程】为什么要选择软件工程专业？

【软件工程】为什么要选择软件工程专业？

个人主页&#xff1a;【&#x1f60a;个人主页】 文章目录前言软件工程&#x1f4bb;&#x1f4bb;&#x1f4bb;就业岗位&#x1f468;‍&#x1f4bb;&#x1f468;‍&#x1f4bb;&#x1f468;‍&#x1f4bb;就业前景&#x1f6e9;️&#x1f6e9;️&#x1f6e9;️工作环…
阅读更多...
趣谈之什么是 API 货币化？

趣谈之什么是 API 货币化？

本文介绍了 API 货币化和 APISIX 实现 API 货币化方法。 作者刘维&#xff0c;API7.ai 技术工程师&#xff0c;Apache APISIX Contributor 原文链接 什么是 API 货币化 想象你开发并部署了一个服务&#xff0c;能够搜集你所在城市所有超市的打折和优惠信息&#xff0c;其他的…
阅读更多...
C生万物 | 校招热门考点 —— 结构体内存对齐

C生万物 | 校招热门考点 —— 结构体内存对齐

文章目录一、前言结构体偏移量计算&#xff1a;offsetof二、规则介绍例题的分解与细说三、习题演练1、练习①2、练习②四、为什么存在内存对齐?1、平台原因(移植原因)2、性能原因五、如何修改默认对齐数六、实战演练✍一道百度笔试题&#xff1a; offsetof 宏的实现&#x1f4…
阅读更多...
深度学习基础篇之深度神经网络（DNN）

深度学习基础篇之深度神经网络（DNN）

神经网络不应该看做是一个算法&#xff0c;应该看做是一个特征挖掘方法。在实际的业界发展过程中&#xff0c;数据的作用往往大于模型&#xff0c;当我们把数据的隐藏特征提取出来之后&#xff0c;用很简单的模型也能预测的很好。 神经网络模型由生物神经中得到启发。在生物神…
阅读更多...
【Linux】Makefile的简述

【Linux】Makefile的简述

目录 前言&#xff1a; 一、Makefile的规则 二、Makefile的函数语法 &#xff08;1&#xff09;通配符pattern ​&#xff08;2&#xff09; 删除clean ​&#xff08;3&#xff09; 立即变量、延时变量 &#xff08;4&#xff09; Makefile常用函数 3-1.Makefile要达到…
阅读更多...
第11章_常用类和基础API

第11章_常用类和基础API

第11章_常用类和基础API 讲师&#xff1a;尚硅谷-宋红康&#xff08;江湖人称&#xff1a;康师傅&#xff09; 官网&#xff1a;http://www.atguigu.com 本章专题与脉络 1. 字符串相关类之不可变字符序列&#xff1a;String 1.1 String的特性 java.lang.String 类代表字符串…
阅读更多...
vue之--使用TypeScript

vue之--使用TypeScript

搭配 TypeScript 使用 Vue​ 像 TypeScript 这样的类型系统可以在编译时通过静态分析检测出很多常见错误。这减少了生产环境中的运行时错误&#xff0c;也让我们在重构大型项目的时候更有信心。通过 IDE 中基于类型的自动补全&#xff0c;TypeScript 还改善了开发体验和效率。…
阅读更多...
2023年美赛春季赛 Y题详细思路

2023年美赛春季赛 Y题详细思路

由于今年各种各样的原因&#xff0c;导致美赛头一次&#xff0c;据说也将是最后一次&#xff0c;临时调整&#xff0c;加设春季赛。这对于急需建模奖项的大家来说是一个很好的机会。无论怎样的原因&#xff0c;今年美赛我们可能有所遗憾。但&#xff0c;春季赛也许就是弥补遗憾…
阅读更多...
HTML4.1表单标签

HTML4.1表单标签

input&#xff08;登录、注册、搜索功能&#xff09; type属性值类型称号展示类型text文本框placeholder占位符password密码框placeholder占位符radio单选框name checked&#xff08;默认选中&#xff09;同类型单选checkbox复选框 checked file 文件选择multiple多文件选择s…
阅读更多...
分类预测 | MATLAB实现CNN-GRU-Attention多输入分类预测

分类预测 | MATLAB实现CNN-GRU-Attention多输入分类预测

分类预测 | MATLAB实现CNN-GRU-Attention多输入分类预测 目录分类预测 | MATLAB实现CNN-GRU-Attention多输入分类预测分类效果模型描述程序设计参考资料分类效果 模型描述 Matlab实现CNN-GRU-Attention多变量分类预测 1.data为数据集&#xff0c;格式为excel&#xff0c;12个输…
阅读更多...
集合-LinkedList

集合-LinkedList

LinkedList LinkedList的概述 LinkedList的底层使用双向链表实现。 链表是一种线性数据结构&#xff0c;其中每个元素都是一个单独的对象&#xff0c;包含一个指向列表中下一个节点的引用。 它可以用于实现各种抽象数据类型&#xff0c;例如列表、堆栈、队列等。 LinkedLis…
阅读更多...
安装Nginx——docker安装

安装Nginx——docker安装

使用docker安装Nginx 1.开启docker systemctl start docker docker search nginx[rootlocalhost ~]# systemctl start docker //开启docker [rootlocalhost ~]# docker search nginx //搜素镜像 2. docker pull nginxdocker imagesdocker run -…
阅读更多...
如何将录音转成文字？

如何将录音转成文字？

在现代社会中&#xff0c;随着语音技术的不断发展和普及&#xff0c;将录音转换为文字变得越来越容易。无论是为了记录会议、面试、讲座、采访&#xff0c;还是为了记录个人的思考和想法&#xff0c;将录音转换为文字是一种方便快捷的方式。本文将介绍几种将录音转换为文字的方…
阅读更多...
计算机系统结构教程-第七章-储存系统笔记（1）

计算机系统结构教程-第七章-储存系统笔记（1）

7.1储存系统的层次结构 概述 理想的储存器&#xff1a;容量大、速度快、价格低。 但以上三种要求在实际应用中是相互矛盾&#xff1a; &#xff08;1&#xff09;速度快&#xff0c;价格高。 &#xff08;2&#xff09;容量大&#xff0c;价格低。 &#xff08;3&#xf…
阅读更多...
ESLint检测VUE和JSON文件

ESLint检测VUE和JSON文件

ESLint 默认只支持检测JS文件中的文件&#xff0c;无法识别其它类型的文件&#xff0c;如果需要检测其它类型的文件就需要安装并指定对应的处理器&#xff0c;有点类似webpack的loader 处理vue文件 使用ESLint默认的处理器处理Vue文件大多数情况下会收到一个这样的错误。 Pa…
阅读更多...
贪心算法

贪心算法

章节目录&#xff1a;一、算法介绍二、应用场景-集合覆盖问题2.1 问题引出2.2 思路分析2.3 代码示例三、结束语一、算法介绍 贪心算法&#xff08;greedy algorithm &#xff0c;又称贪婪算法&#xff09;是指&#xff0c;在对问题求解时&#xff0c;总是做出在当前看来是最好的…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023