paper:http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
本文提出的对比损失contrastive loss被广泛应用于自监督模型中,但最初对比损失是作为一个特征降维方法而提出的。
摘要
降维是学习一种映射关系,通过这种映射关系,将一组高维输入点映射到一个低维流形上,输入空间中的“相似”点映射到流形上后对应点之间的距离比较近。大多数现有的降维方法存在两个缺点,一是它们中的大多数都依赖于输入空间中一个有意义并且可计算的距离度量,二是它们没有计算一个可以精确地映射新的输入样本的“函数”,这些新的输入样本和训练样本的关系是未知的。
本文提出了一种通过学习不变映射的降维方法(Dimensionality Reduction by Learning an Invariant Mapping, DrLIM)来学习一个全局相关非线性映射函数,从而将数据均匀地映射到输出流形。这种学习仅依赖于邻域关系而不需要输入空间中的任何距离度量。通过实验证明,该方法可以学习到对输入某些变换的不变映射。
现有方法存在的问题
当前大多数降维方法存在两点不足,一是它们无法生成一个函数或映射可以应用于与训练样本关系未知的新样本,二是许多方法都假设输入空间中存在一个有意义并且可计算的距离度量。
当前方法的另一个局限性是,它们倾向于在输出空间中聚类点,有时点的分布过于密集,可能会被认为是退化解。而大家更希望找到一个被样本均匀覆盖的流形。
本文的创新点
本文提出的Dimensionality Reduction by Learning an Invariant Mapping (DrLIM),为上述问题提供了一种解决方法。DrLIM是一种学习全局相关非线性函数的方法,该函数将数据映射到一个低维流形。该方法具有四个基本特征:
- 它只需要训练样本之间的邻域关系。这些关系可以来自先验知识或手动标记,并且独立于任何距离度量。
- 它可以学习具有对输入的复杂非线性变化的不变性的函数,如照明变化和几何畸变。
- 学习到的函数在没有先验知识的情况下,可以用来映射在训练过程中没有见过的新样本。
- 由函数生成的映射在某种意义上在输出空间中是“平滑的”和连贯的。
方法介绍
本文提出了一种新的损失函数 - 对比损失函数contrastive loss,通过拉进邻域样本之间的距离拉远非邻域样本之间距离的方式,来学习参数化函数 \(G_{W}\) 的参数 \(W\)。先验知识可以用来判断样本间的邻域关系。
考虑一组高维训练向量 \(\vec{X}_{i} \) 的集和 \(\mathcal{I}\),假设对于每个 \(\vec{X}_{i}\in \mathcal{I}\) 都有一组训练向量 \(S_{\vec{X}_{i} }\) 与之相似。这个相似向量集和可以通过先验知识得到,例如对distortion或temporal proximity的不变性,而不是基于一个简单的距离。一个有意义的映射会将输入空间中相似的向量映射成输出流形中距离相近的点,将不相似的向量映射为距离较远的点。本文提出的对比损失和传统的损失不同,之前的损失函数遍历所有样本计算和对应GT之间的损失然后求和,而对比损失是计算两两样本对之间的损失。假设 \(\vec{X}_{1},\vec{X}_{2}\in \mathcal{I} \) 是一对输入向量,\(Y\) 是分配给这对向量的二进制标签,如果 \(\vec{X}_{1},\vec{X}_{2}\) 是相似的,\(Y=1\),反之 \(Y=0\)。定义 \(\vec{X}_{1},\vec{X}_{2}\) 之间需要学习的参数化距离 \(D_{W}\) 为 \(G_{W}\) 的输出之间的欧式距离
![]()
为了简便,\(D_{W}(\vec{X}_{1},\vec{X}_{2})\) 记为 \(D_{W}\),对比损失的通用形式如下
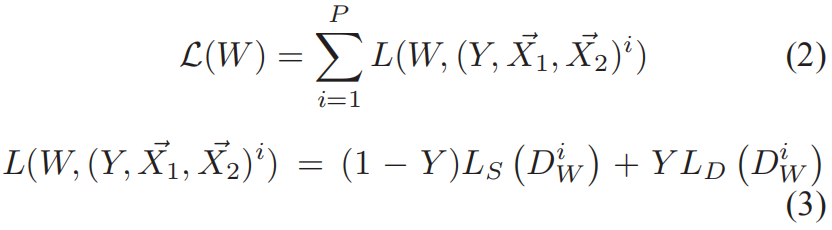
其中 \((Y,\vec{X}_{1},\vec{X}_{2})^{i}\) 是第 \(i\) 对有标签样本,\(L_{S}\) 是一对相似样本点的偏损失函数,\(L_{D}\) 是一对不相似样本点的偏损失函数,\(P\) 是训练样本对的数量(它可能和样本数量的平方一样大)。
\(L_{S}\) 和 \(L_{D}\) 的设计必须使最小化 \(L\) 等价于减小相似样本对的 \(D_{W}\),增大非相似样本对的 \(D_{W}\)。
损失函数的具体形式如下
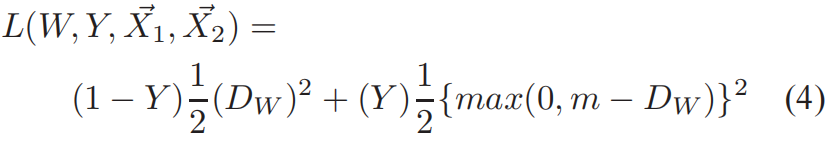
其中 \(m>0\) 是一个边界值,它定义了 \(G_{W}(\vec{X})\) 周围的一个半径。不相似的样本对只有它们的距离在这个半径范围内时才会对损失函数有贡献,如下图所示。
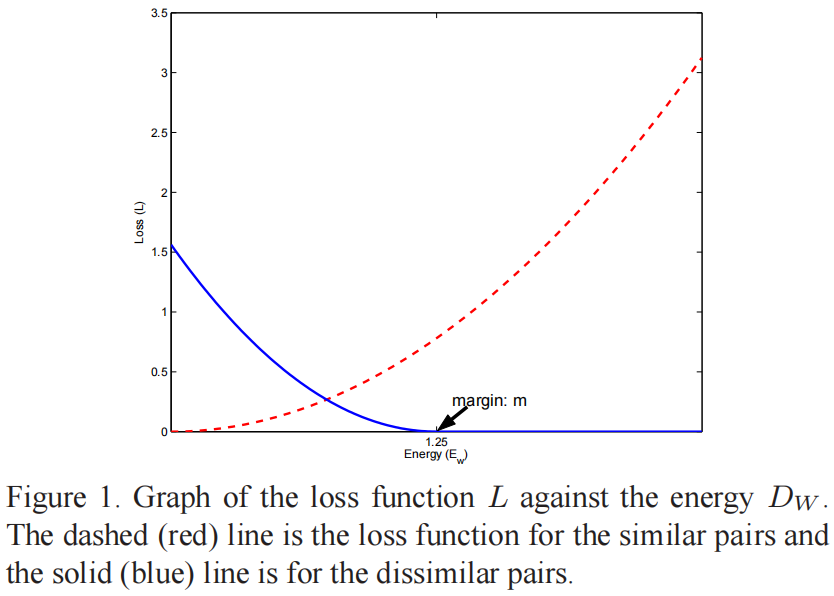
其中关于不相似样本对的对比项 \(L_{D}\) 是至关重要的,只在所有的相似样本对集合上最小化 \(D_{W}(\vec{X}_{1},\vec{X}_{2})\) 通常会得到一个崩溃解,因为可以通过将 \(G_{W}\) 设为一个常数从而使 \(D_{W}\) 和损失 \(L\) 都变为0。
算法流程