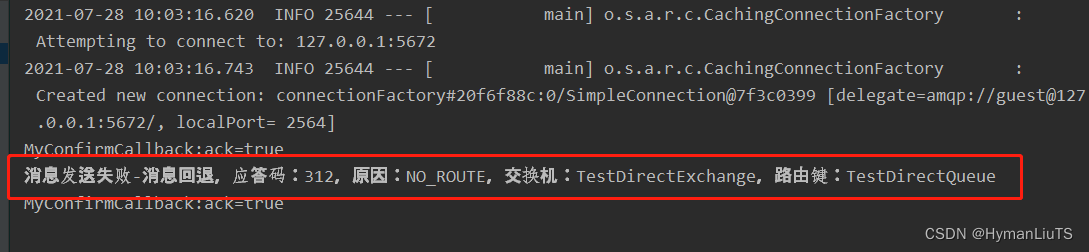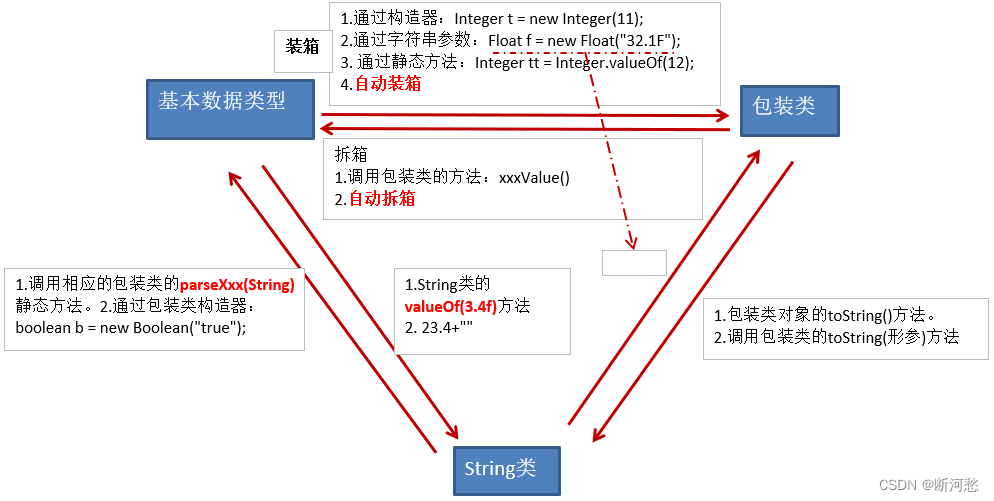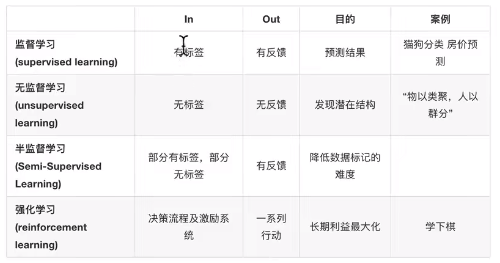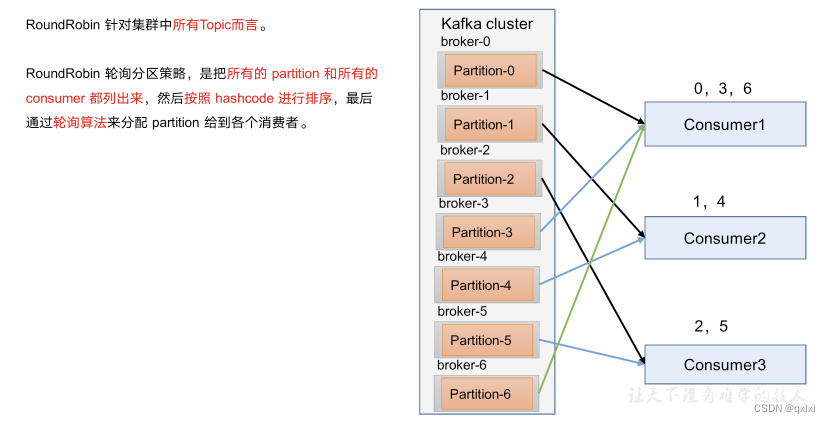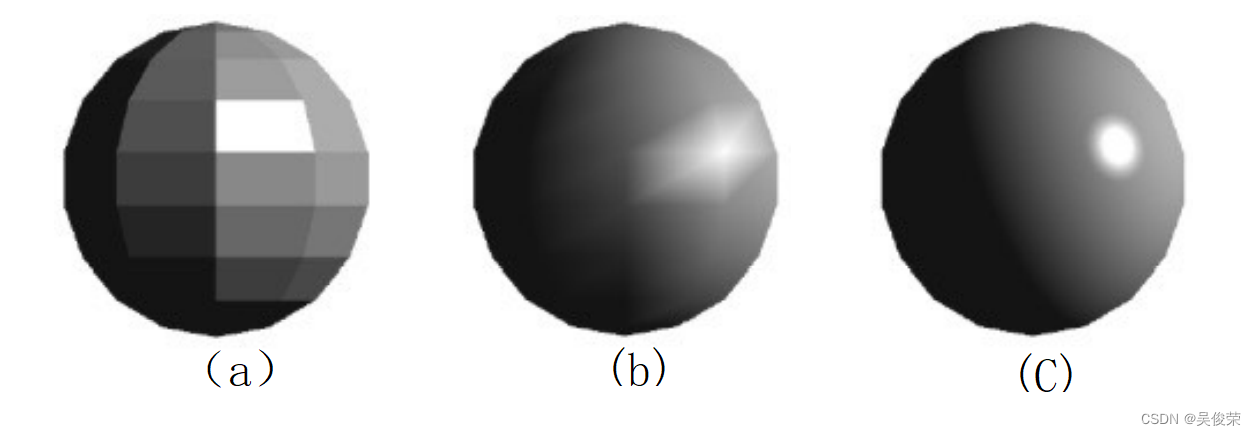
a:平面法线着色
b:顶点法线着色
c:像素着色

平面法线（face normal,由于在计算机几何学中法线是有方向的向量，所以也有将normal译作法向量）

是 一种描述多边形朝向（即正交于多边形上所有点）的单位向量。

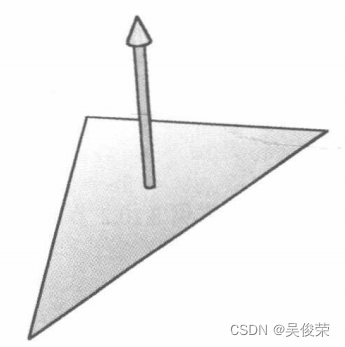
曲面法线（surface normal）

是 一种垂直于曲面上一点处切平面（有文献强调还要满足曲面发现经过该点这一条件件）的单位向量

对于光照计算来说，我们需要通过三角形网格曲面上每一点处的曲面法线来确定光线照到对应点上 的角度。为了求出曲面法线，我们仅先指定位于网格顶点处的曲面法线(所以也将之称作顶点法线，vertex normal )。接下来，为取得三角形网格曲面上每个点处的近似曲面法线，在三角形进行光栅化过程的中对 这些顶点法线进行插值计算

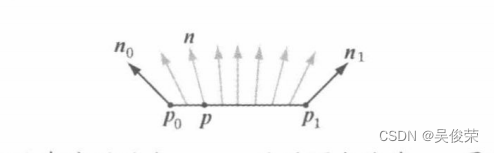
n0与n1分别是定义在线段端点p0、p1处的顶点法线。n是经此线段端点向量插值(加权平均值)所得到的点p处的法向量。即n=n0+t(n1-n0),这里的，满足p = p0+t(p1-p0)。

计算法向量

为了找到三角形Δp0p1p2的平面法线，我们首先计算位于三角形边上的两个向量：

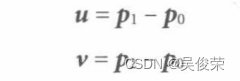那么，此三角形的平面法线即为：

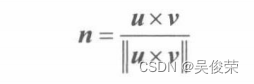
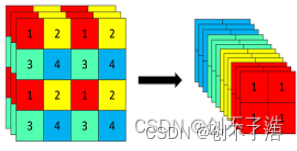
对于可微的光滑曲面而言，我们可以利用微积分方面的知识来 求出曲面点处的法线。但问题在于，三角形网格运用一种被称为求 顶点法线平均值(vertex normal averaging )的计算方法。此方法通过 对网格中共享顶点 v 的多边形的平面法线求取平均值，从而获得网 格中任意顶点 v 处的顶点法线n。例如，在图中，

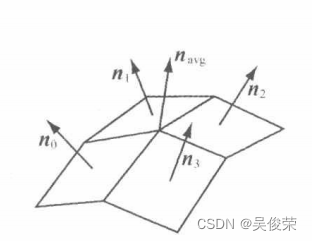
位于中间的顶点被四个多边形所共用，所以可通过计算这4个多边形平面法线的平均值来求取中间顶点处的近似法线

网格中的四个 多边形共用顶点v ，因此，v 处的顶点法线求法如下：

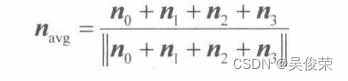
在上面这个例子中，由于我们对求和的结果已进行了规范化处 理，因此便无需像往常求算术平均值那样再除以4。注意，为了得 到更为精准的结果，我们还可以釆用更加复杂的求平均值方法，比如说，根据多边形的面积来确定权 重(如面积大的多边形的权重要大于面积小的多边形)，以求取加权平均值。

变换法向量

思考图a。图中,切向量（tangent vector ） u=V1-V0 正交于法向量（normal vector ） n 。如果对此 应用一个非等比缩放变换A,则可从图b看到，变换后的切向量uA =v1A-V0A没能继续保持与变换 后法向量nA的正交性。

切向量与法向量的变换

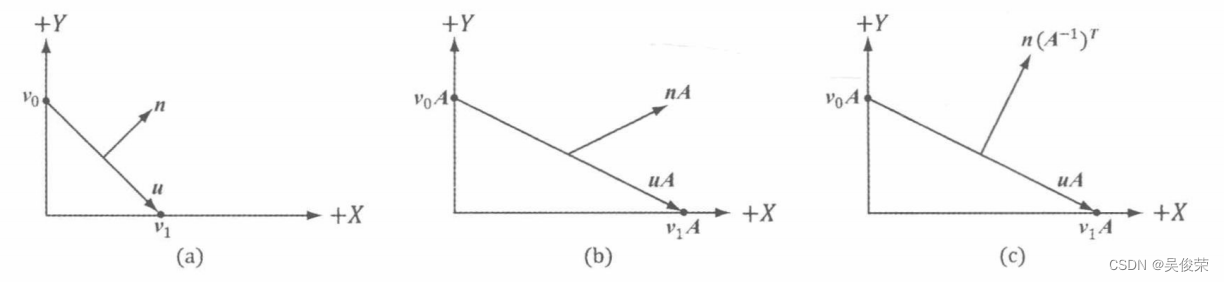
（a ）切向量与法向量在变换前的正交关系

（b ）经过在x轴正方向放大两倍的处理后，法向量
不再与切向量保持正交关系

（c）通过对法向量进行图b中缩放变换的逆转置矩阵运算后，法向量与切向量重归正交关系

所以，我们现在所面对的问题是，若给定一个用于变换点与向量（非法线）的变换矩阵A,如何能 够求出这样一个变换矩阵B：通过它来变换法向量，使经矩阵A变换后的切向量与法向量重归正交的关 系（即uA•nB=0 ）。为此，我们首先从已知的信息着手，如果法向量n正交于切向量u则有：

尽管运用了逆转置变换，但法向量仍可能会失去其单位长度。所以在变换完成后，可能需 对它再次进行规范化处理。