机器学习异常值检测与处理

news2025/1/14 0:53:15

文章目录

一、异常值检测
- 1.1 简单统计
- 1.2 3σ原则检测
- 1.3 箱线图检测
- 1.4 DBScan密度聚类
二、异常值处理

异常值是指不属于某一特定群体的数据点。它是一个与其他数值大不相同的异常观测值，与良好构成的数据组相背离。在机器学习建模准备数据集时，检测出所有的异常值，并且要么移除它们、要么分析它们来了解它们最初存在的原因是非常重要的。

一、异常值检测

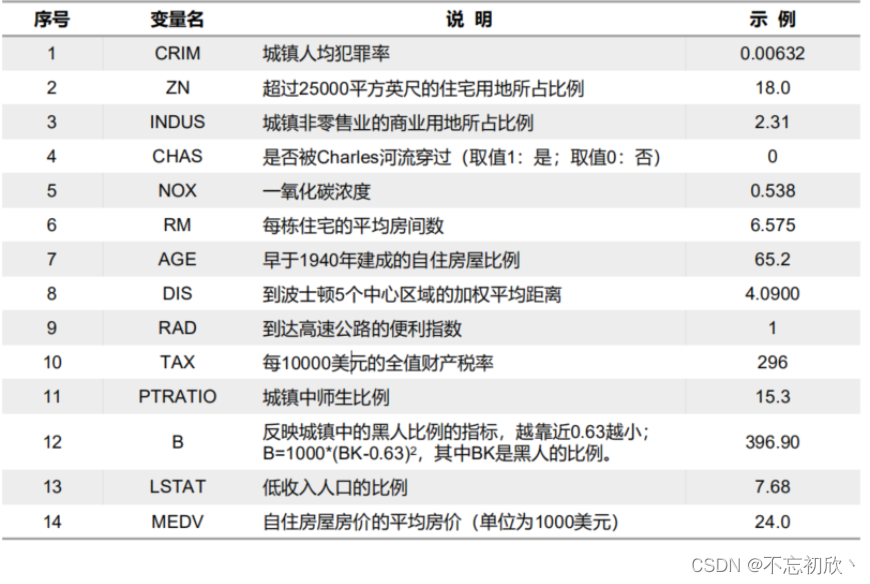
波士顿房价数据集

卡内基梅隆大学，StatLib库，1978年，涵盖了麻省波士顿的506个不同郊区的房屋数据。
404条训练数据集，102条测试数据集。
每条数据14个字段，包含13个属性，和一个房价的平均值。

在这里插入图片描述

1.1 简单统计

在实际工作中，表中会有很多脏数据，对特征值进行简单统计之后，结合业务及自己的经验，分析某些特征是否存在异常值和异常值是什么。例如有一个特征是人的身高，出现了一个大于5m的数值，根据常识肯定是异常值；特征性别，假设出现了男女之外的情况，也是异常值等等。

1.2 3σ原则检测

在统计学中，如果一个数据分布式近似正态分布，那么大约68%的数据值在平均值的前后一个标准差范围内，大约95%的数据值在平均值的前后两个标准差范围内，大约99.7%的数据值在前后三个标准差的范围内。在3σ原则下，异常值如超过3倍标准差，那么可以将其视为异常值。

数值分布	在数据中的占比
(μ-σ,μ+σ)	0.6827
(μ-2σ,μ+2σ)	0.9545
(μ-3σ,μ+3σ)	0.9973

注意：在正态分布中σ代表标准差，μ代表均值，x=μ为图形的对称轴

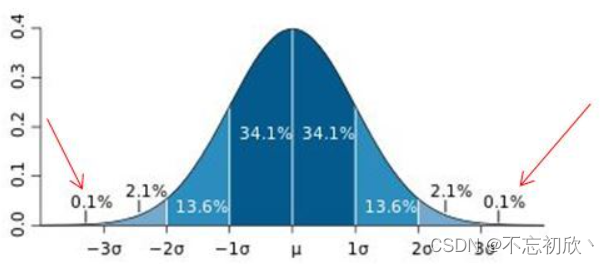
在这里插入图片描述
红色箭头所指的数据在正负3σ之外，因此是异常值。

import numpy as np
import pandas as pd
from sklearn import datasets


def three_sigma(Ser1):
    '''
    3σ法则识别异常值函数
    Ser1：表示传入DataFrame的某一列。
    '''
    rule = (Ser1.mean()-3*Ser1.std()>Ser1) | (Ser1.mean()+3*Ser1.std()< Ser1)
    index = np.arange(Ser1.shape[0])[rule]
    outrange = Ser1.iloc[index]
    return outrange


if __name__ == '__main__':
    boston_data = datasets.load_boston()
    df = pd.DataFrame(boston_data.data, columns=boston_data.feature_names)
    # 对犯罪率这里列进行3σ法则识别，把不遵守正太分布的数据挑选出来
    data = three_sigma(df['CRIM']).head()
    print(data)

输出结果如下：

[5 rows x 13 columns]
380    88.9762
398    38.3518
404    41.5292
405    67.9208
410    51.1358
Name: CRIM, dtype: float64

1.3 箱线图检测

和3σ原则相比，箱线图依据实际数据绘制，真实、直观地表现出了数据分布的本来面貌，且没有对数据作任何限制性要求（3σ原则要求数据服从正态分布或近似服从正态分布），其判断异常值的标准以四分位数和四分位距为基础。四分位数给出了数据分布的中心、散布和形状的某种指示，具有一定的鲁棒性，即25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值通常不能对这个标准施加影响。由于箱线图识别异常值的结果比较客观，因此在识别异常值方面具有一定的优越性。

箱型图提供了识别异常值的一个标准，即异常值通常被定义为小于QL-1.5IQR或大于QU+1.5IQR的值。

QL：下四分位数Q1，表示全部观察值中有四分之一的数据取值比它小，数据的1/4位置；
QU：上四分位数Q3，表示全部观察值中有四分之一的数据取值比它大，数据的3/4位置；
IQR：四分位数间距，是上四分位数QU与下四分位数QL之差（Q3-Q1），其间包含了全部观察值的一半。
下须：下须是非异常值范围内的最小值，等于QL-1.5IQR；
上须：上须是非异常范围内的最大值，等于Q3+1.5IQ3

在这里插入图片描述

画图展示

import seaborn as sns
ax = sns.boxplot(y=df["CRIM"])

箱线图如下：
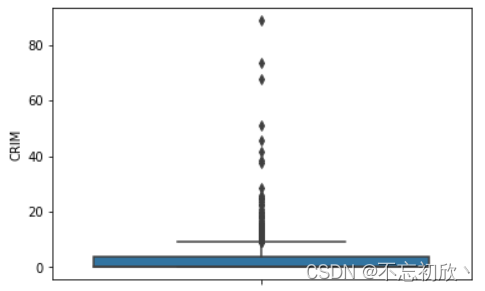
在这里插入图片描述
从箱线图可以看出大于8左右的都为异常值

使用代码检测

def box_plot(Ser):
    '''
    箱线图法检测异常值函数
    Ser：进行异常值分析的DataFrame的某一列
    '''
    Low = Ser.quantile(0.25)-1.5*(Ser.quantile(0.75)-Ser.quantile(0.25))
    Up = Ser.quantile(0.75)+1.5*(Ser.quantile(0.75)-Ser.quantile(0.25))
    index = (Ser< Low) | (Ser>Up)
    Outlier = Ser.loc[index]
    return(Outlier)


if __name__ == '__main__':
    boston_data = datasets.load_boston()
    df = pd.DataFrame(boston_data.data, columns=boston_data.feature_names)
    data = box_plot(df['CRIM']).head()
    print(data)

识别结果如下：

367    13.5222
371     9.2323
373    11.1081
374    18.4982
375    19.6091
Name: CRIM, dtype: float64

从代码打印的5个结果来看，均符合箱线图展示结果

1.4 DBScan密度聚类

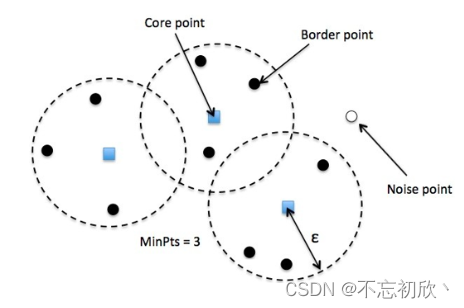
DBScan是一种被用于基于密度的对于一维或多维数据的异常检测方法，DBScan有三个重要概念：

核心点：为了理解核心点，我们需要访问一些用于定义DBScan工作的超参数。第一个超参数是最小值样本（min_samples）。这只是形成集聚的核心点的最小数量。第二重要的超参数eps，它是两个被视为在同一个簇中的样本之间的最大距离。
边界点：是与核心点在同一集群的点，但是要离集群中心远得多。
其他的点：称为噪声点，那些数据点不属于任何集群。它们可能是异常点，可能是非异常点，需要进一步调查。现在让我们看看代码。

在这里插入图片描述

import numpy as np
from sklearn.cluster import DBSCAN

# 设置随机数种子
np.random.seed(1)
random_data = np.random.randn(50000, 2) * 20 + 20

outlier_detection = DBSCAN(min_samples=2, eps=3)
clusters = outlier_detection.fit_predict(random_data)
print(list(clusters).count(-1))

# 94