“韩信点兵”蓝桥杯问题描述:
“蓝桥杯”中有一道有趣的 Scratch 编程题,题目要求为:韩信点兵
扩展知识:
这道题叫“中国余数定理”,又叫“孙子定理”,也叫“韩信点兵问题”,是我国古代数学智慧结晶。

解题思路及方法
第一种题目及解题方法
有一个数,除以3余下2,除以5余下2,除以7余下2。求这个数最小值。
先将这个数设为 x ,不难发现只要 x 减去 2 ,就变成 3、5、7 的公倍数。通过计算可知:3、5、7最小公倍数是 105。在加上原先去掉的 2 ,答案为 107。
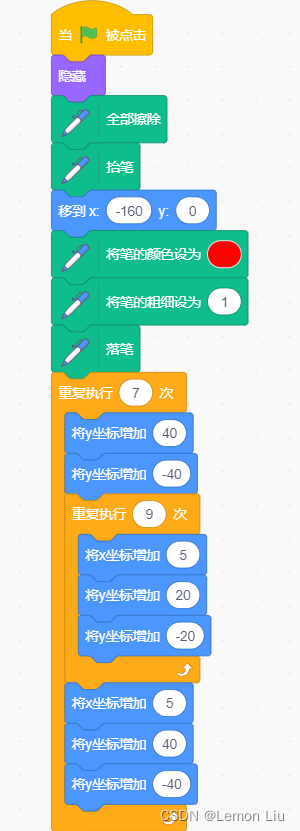
代码图片如下:
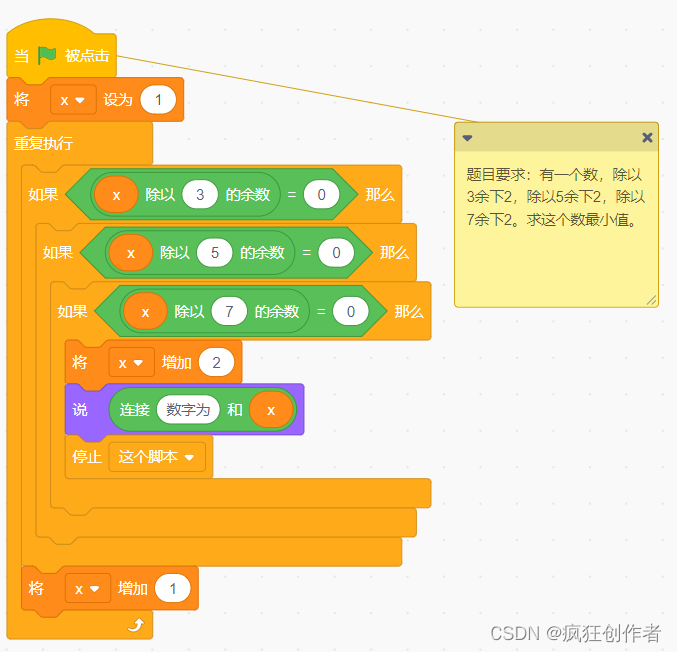
比较机智的网友,还可以用算式算出 3、5、7 的最小共公倍数。因为 3、5、7 这三数为互质关系。如下:
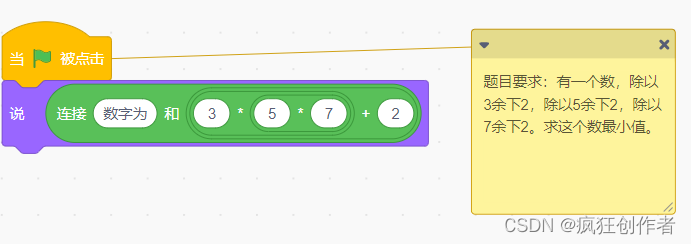
第二种题目及解题方法
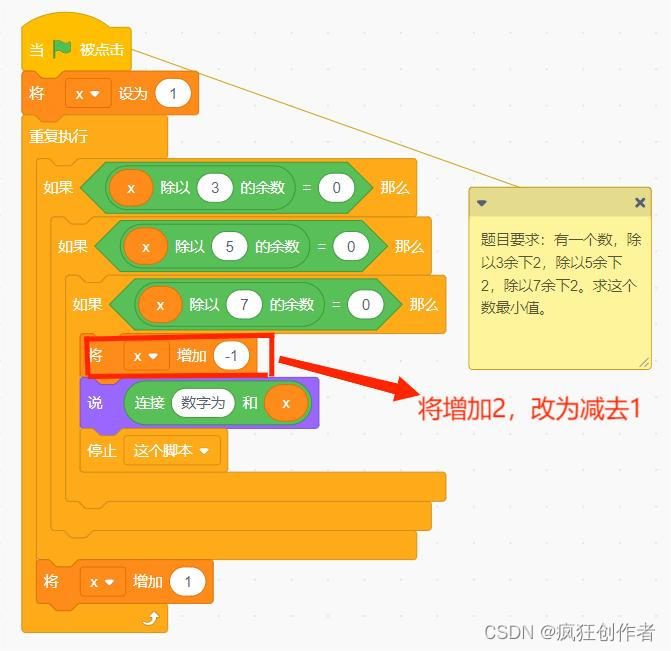
有一个数,除以3余2,除以5余4,除以7余6。求这个数最小值。
还是将这个数设为 x ,仔细查看即可发现只要将最后剩的余数加 1,就可以将结果变作整数。也就是说,将 x 增加 1 ,就变成 3、5、7 的公倍数。通过计算可知:3、5、7最小公倍数是 105。在去掉原先加上的 1 ,答案为 104.
算式如下:
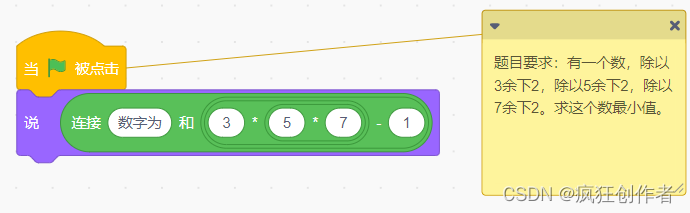
第三种题目及解题方法
有一个数,除以3余2,除以5余3,除以7余1。求这个数最小值。
仍旧将这个数设为 x ,聪明的网友可能看出了规律:除以 7 余 1 相当于除以 7 “余 8 ”,除以 5 余 3 也相当于 “余 8 ”,除以 3 余 2 还相当于“余 8 ”。知道了这点,就可以通过“第一种题目及解题方法”解决这个问题。最后不要忘了加上 8。
代码小编也就不写了,请您看上两种解题方法,写出代码。

第四种题目及解题方法
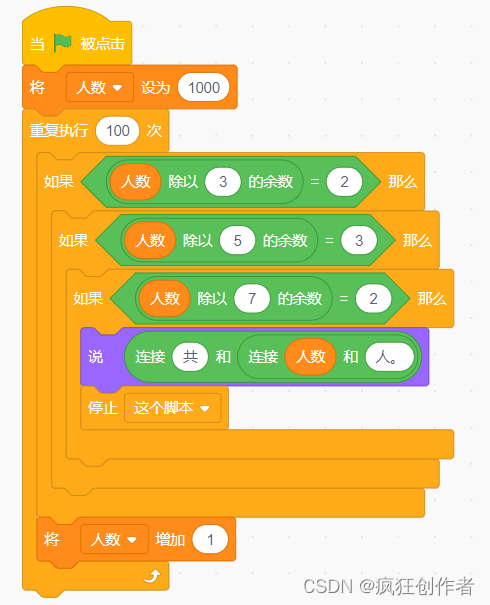
背景:在秦末时期,楚汉相争。韩信曾有一次带 1500 名兵士打仗,战死四五百人。这是,前方来报,说敌军率 500 人前来进攻。为了统计剩余士兵的个数,韩信令士兵 3 人一排,多出 2 人;5 人一排,多出 3 人;7 人一排,多出 2 人。韩信据此很快说出人数:1049 人。那么请问,韩信是如何快速知道军队人数的呢?
这道题可以使用“重复执行”,将 1000~1100 逐个判断是否符合要求。全部代码如下:
第五种题目及解题方法
古代明朝数学家程大位将解法编成易于上口的《孙子歌诀》:
三人同行七十稀,五树梅花廿一支。
七子团圆正半月。除百零五使得知。
逐字逐句分析整首歌诀:
三人同行七十稀:把除以 3 所得的余数 (上文的“ 3 人一排,多出 2 人”) 乘以 70。
五树梅花廿一支:把除以 5 所得的余数 (上文的“ 3 人一排,多出 2 人”) 乘以 70。
七子团圆正半月:把除以 7 所得的余数 (上文的“ 3 人一排,多出 2 人”) 乘以 15 (“ 正半月”指 15 天)。
除百零五便得知:把上述三个积加起来,除以 105 (“百零五”指 105 ) 的余数便是答案。
列式:
2×70+3×21+2×15=233 233÷105=2……23
答案便是 23
解题原理:
问题:
- 为什么 70,21,15,105 有如此神奇作用?
- 70,21,15,105 是从何而来?
70,21,15,105 的性质:
- 70 除以 3 余 1,被 5和7整除,所以 70a 除以 3 余 a ,也被 5和7整除;
- 21 余以 5 余 1,被 3和7整除,所以 21b 除以 5 余 b ,也被 3和7整除;
- 15 除以 7 余 1,被 3和5整除,所以 15c 除以 7 余 c ,也被 3和5 整除。
- 而 105 则是 3,5,7 的最小公倍数。
总之来说,70a+21b+15c 是被 3 除余 a,被 5 除余 b ,被 7 除余 c 的数,这个数如果大了,还要减去它们的公倍数。
另一种解法:
现在我们来提出另外一种解法,本质上是换汤不换药,请大家不妨仔细体会一下。
题目为:“今有物不知数,五五数之余二,七七数之余二,九九数之余四,问物几何?”
先找除以 9 余 4 的数:4,13,22,31,40,49,58,67……
其中除以 7 余 2 的数有:58
但是 58 除以 5 不会余 2,用 58 加上7 和 9 的最小公倍数 63,直到到除以 5 后余数为 2为止:58,121,184,247……