一、简介和环境准备

简介：

环境：

二、实战演练

2.1使用葡萄（Wine）数据集，进行贝叶斯分类

1.数据导入

2.模型训练

3.模型预测

2.2模拟离散数据集–贝叶斯分类

1.数据导入、分析

2.模型训练、预测

三、原理解析

朴素贝叶斯算法

优缺点：

一、简介和环境准备

简介：

朴素贝叶斯（Naive Bayes, NB) 是机器学习中一种基于贝叶斯定理的分类算法。它假设输入的特征之间相互独立且对分类结果的影响是等同的，因此称为朴素贝叶斯。

具体来说，它通过计算先验概率和条件概率来确定输入样本所属的分类，其中先验概率指的是每个分类在整个数据集中出现的概率，条件概率指的是给定某个分类的情况下，输入样本在各个特征上的概率分布。

在实际应用中，朴素贝叶斯常用于文本分类、垃圾邮件过滤等任务中，具有计算速度快、对数据量不敏感等优点。

贝叶斯公式是英国数学家提出的一个数据公式:

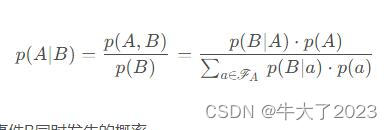
p(A,B)：表示事件A和事件B同时发生的概率。

p(B)：表示事件B发生的概率，叫做先验概率；p(A)：表示事件A发生的概率。

p(A|B)：表示当事件B发生的条件下，事件A发生的概率叫做后验概率。

p(B|A)：表示当事件A发生的条件下，事件B发生的概率。

我们用一句话理解贝叶斯：世间很多事都存在某种联系，假设事件A和事件B。人们常常使用已经发生的某个事件去推断我们想要知道的之间的概率。
例如，医生在确诊的时候，会根据病人的舌苔、心跳等来判断病人得了什么病。对病人来说，只会关注得了什么病，医生会通道已经发生的事件来
确诊具体的情况。这里就用到了贝叶斯思想，A是已经发生的病人症状，在A发生的条件下是B_i的概率。

环境：

pycharm，建议：

1. python3.7
2. numpy >= '1.16.4'
3. sklearn >= '0.23.1'

二、实战演练

数据集都是能调用的，不用另下载。这里简单介绍一下sklearn的datasets。

scikit-learn（sklearn）中提供了多个现成的数据集，可以用于机器学习任务和演示。目前（2021年），sklearn中提供的数据集有以下20个：

波士顿房价数据集（Boston Housing）
Iris数据集（Iris）
糖尿病数据集（Diabetes）
手写数字数据集（Digits）
乳腺癌数据集（Breast Cancer）
威斯康星州乳腺癌数据集（Wisconsin Breast Cancer）
Linnerud体能训练数据集（Linnerud）
瑞士银行家数据集（Swiss Banknotes）
20类新闻文本数据集（20 newsgroups）
Olivetti脸部图像数据集（Olivetti faces）
口袋妖怪数据集（Pokemon）
森林覆盖类型数据集（Forest Covertypes）
加州房价数据集（California Housing）
远红外线数据集（Infrared）
垃圾邮件数据集（Spam）
面部识别数据集（Faces）
KDD Cup 1999网络入侵检测数据集（KDD Cup 1999）
索引指数数据集（Digits）
贷款违约数据集（Credit Default）
新冠病毒诊断数据集（Covid-19）

除了这些现成的数据集，sklearn还提供了一些工具可以生成人造数据集，如make_classification，make_regression和make_blobs等。

2.1使用葡萄（Wine）数据集，进行贝叶斯分类

1.数据导入

import warnings
warnings.filterwarnings('ignore')
import numpy as np
# 加载莺尾花数据集
from sklearn import datasets
# 导入高斯朴素贝叶斯分类器
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split

X, y = datasets.load_wine(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

我们需要计算两个概率分别是：条件概率：P ( X ( i ) = x ( i ) ∣ Y = c k )和类目c k 的先验概率：P(Y=c k)。
通过分析发现训练数据是数值类型的数据，这里假设每个特征服从高斯分布，因此我们选择高斯朴素贝叶斯来进行分类计算。

2.模型训练

# 使用高斯朴素贝叶斯进行计算
clf = GaussianNB(var_smoothing=1e-8)
clf.fit(X_train, y_train)

3.模型预测

# 评估
y_pred = clf.predict(X_test)
acc = np.sum(y_test == y_pred) / X_test.shape[0]
print("Test Acc : %.3f" % acc)

# 预测
y_proba = clf.predict_proba(X_test[:1])
print(clf.predict(X_test[:1]))
print("预计的概率值:", y_proba)

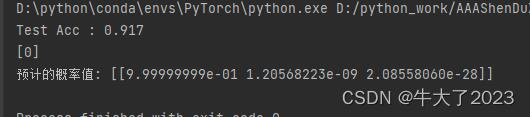
高斯朴素贝叶斯假设每个特征都服从高斯分布，我们把一个随机变量X服从数学期望为μ，方差为σ2的数据分布称为高斯分布。对于每个特征我们一般使用平均值来估计μ和使用所有特征的方差估计σ2。

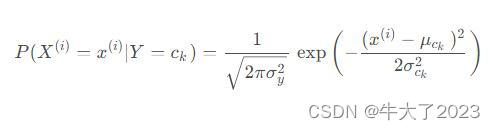
从上述例子中的预测结果中，我们可以看到类别0对应的后验概率值最大，所以我们认为类目2是最优的结果。

这个举一反三很容易，改变导入数据库即可，再看接下来离散数据集的分类。

2.2模拟离散数据集–贝叶斯分类

1.数据导入、分析

import random
import numpy as np
# 使用基于类目特征的朴素贝叶斯
from sklearn.naive_bayes import CategoricalNB
from sklearn.model_selection import train_test_split

随机生成数据进行训练，可以自己diy

# 模拟数据
rng = np.random.RandomState(1)
# 随机生成500个100维的数据，每一维的特征都是[0, 10]之前的整数
X = rng.randint(11, size=(500, 100))
y = np.array([1, 2, 3, 4, 5] * 100)
data = np.c_[X, y]
# X和y进行整体打散
random.shuffle(data)
X = data[:,:-1]
y = data[:, -1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

X和y代表一个特征矩阵和一个目标向量。

X是一个形状为（500，100）的二维数组，其中包含500个样本，每个样本包含100个特征。这个特征矩阵是使用numpy的randint函数从0到10（不包括11）的均匀分布中生成的随机整数。

y是一个形状为（500，）的一维数组，其中包含500个目标值。这些目标值分别为1，2，3，4，5，重复100次，与特征矩阵中的样本一一对应。在机器学习任务中，通常需要使用特征矩阵和目标向量来训练和测试模型，以便对新的未知数据进行预测。

2.模型训练、预测

所有的数据特征都是离散特征，我们引入基于离散特征的朴素贝叶斯分类器。

clf = CategoricalNB(alpha=1)
clf.fit(X_train, y_train)
acc = clf.score(X_test, y_test)
print("Test Acc : %.3f" % acc)

# 随机数据测试，分析预测结果，贝叶斯会选择概率最大的预测结果
# 比如这里的预测结果是7，7对应的概率最大，由于我们是随机数据
# 读者运行的时候，可能会出现不一样的结果。
x = rng.randint(5, size=(1, 100))
print(clf.predict_proba(x))
print(clf.predict(x))

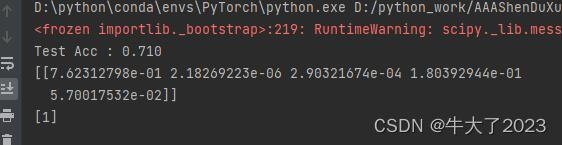
可以看到测试的数据的结果，贝叶斯会选择概率最大的预测结果，比如这里的预测结果是7，7对应的概率最大，由于我们是随机数据，读者运行的时候，可能会出现不一样的结果。

同时注意第一行有个变量alpha，当alpha=0时，就是极大似然估计。通常取值alpha=1，这就是拉普拉斯平滑(Laplace smoothing)，这有叫做贝叶斯估计，主要是因为如果使用极大似然估计，如果某个特征值在训练数据中没有出现，这时候会出现概率为0的情况，导致整个估计都为0，因为引入贝叶斯估计。

这里的测试数据的准确率没有任何意义，因为数据是随机生成的，不一定具有贝叶斯先验性，这里只是作为一个例子。

三、原理解析

朴素贝叶斯算法

朴素贝叶斯法 = 贝叶斯定理 + 特征条件独立。

输入 $X \in R^n$ 空间是n维向量集合，输出空间 $y=\{c_1,c_2,...,c_K\}$ . 所有的X和y都是对应空间上的随机变量. P(X,Y)是X和Y的联合概率分别. 训练数据集(由P(X,Y)独立同分布产生):
$T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$

原文说的比较详细，这里不再赘述，可以看文末链接。

总结一下就是在分类时，它通过计算样本特征对于各个类别的条件概率，从而选择概率最大的类别作为预测结果。而且条件独立互不影响。

优缺点：

优点：
朴素贝叶斯算法主要基于经典的贝叶斯公式进行推倒，具有很好的数学原理。而且在数据量很小的时候表现良好，数据量很大的时候也可以进行增量计算。由于朴素贝叶斯使用先验概率估计后验概率具有很好的模型的可解释性。

缺点：
朴素贝叶斯模型与其他分类方法相比具有最小的理论误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下，假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进，例如为了计算量不至于太大，我们假定每个属性只依赖另外的一个。解决特征之间的相关性，我们还可以使用数据降维(PCA)的方法，去除特征相关性，再进行朴素贝叶斯计算。

原文：A.机器学习入门算法（二）: 基于朴素贝叶斯(Naive Bayes)的分类预测_汀、人工智能的博客-CSDN博客