1.遗传算法定义

遗传算法（Genetic Algorithm, GA）起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。
遗传算法（Genetic Algorithm, GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。

2.相关术语

基因型(genotype)：性状的内部表现。

表现型(phenotype)：性状的外部表现。

进化(evolution)：种群逐渐适应生存环境，品质不断得到改良。生物的进化是以种群的形式进行的。

适应度(fitness)：度量某个物种对于生存环境的适应程度。

选择(selection)：以一定的概率从种群中选择若干个个体。一般，选择过程是一种基于适应度的优胜劣汰的过程。

复制(reproduction)：细胞分裂时，遗传物质DNA通过复制而转移到新产生的细胞中，新细胞就继承了旧细胞的基因。

交叉(crossover)：两个染色体的某一相同位置处DNA被切断，前后两串分别交叉组合形成两个新的染色体。也称基因重组或杂交；

变异(mutation)：复制时可能（很小的概率）产生某些复制差错，变异产生新的染色体，表现出新的性状。

编码(coding)：DNA中遗传信息在一个长链上按一定的模式排列。遗传编码可看作从表现型到基因型的映射。

解码(decoding)：基因型到表现型的映射。

个体（individual）：指染色体带有特征的实体；

种群（population）：个体的集合，该集合内个体数称为种群的大小。

遗传算法中每一条染色体，对应着遗传算法的一个解决方案，一般我们用适应性函数（fitness function）来衡量这个解决方案的优劣。所以从一个基因组到其解的适应度形成一个映射。可以把遗传算法的过程看作是一个在多元函数里面求最优解的过程。可以这样想象，这个多维曲面里面有数不清的“山峰”，而这些山峰所对应的就是局部最优解。而其中也会有一个“山峰”的海拔最高的，那么这个就是全局最优解。而遗传算法的任务就是尽量爬到最高峰，而不是陷落在一些小山峰。（另外，值得注意的是遗传算法不一定要找“最高的山峰”，如果问题的适应度评价越小越好的话，那么全局最优解就是函数的最小值，对应的，遗传算法所要找的就是“最深的谷底”）

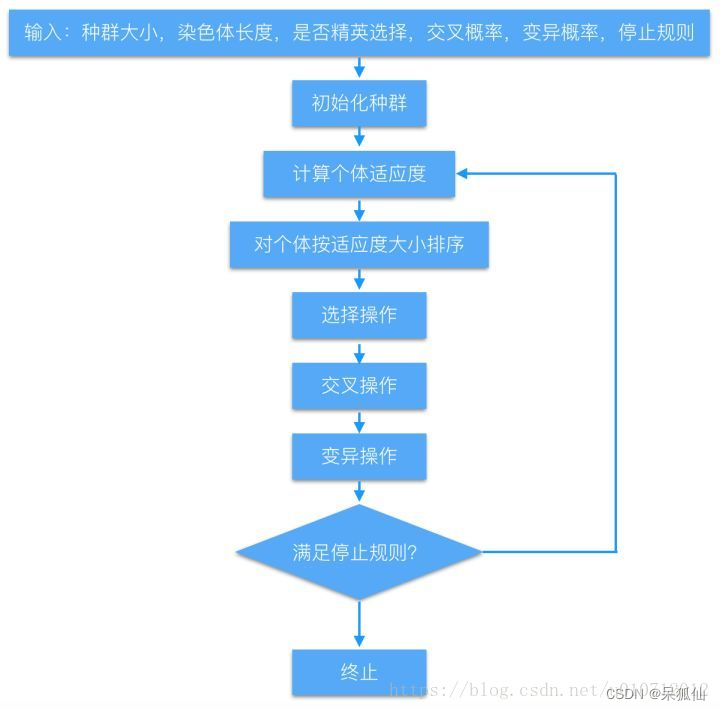
3.遗传算法的主要步骤

（1）编码：将问题的候选解用染色体表示，实现解空间向编码空间的映射过程。遗传算法不直接处理解空间的决策变量，而是将其转换成由基因按一定结构组成的染色体。编码方式有很多，如二进制编码、实数向量编码、整数排列编码、通用数据结构编码等等。本文将采用二进制编码的方式，将十进制的变量转换成二进制，用0和1组成的数字串模拟染色体，可以很方便地实现基因交叉、变异等操作。

（2）种群初始化：产生代表问题可能潜在解集的一个初始群体（编码集合）。种群规模设定主要有以下方面的考虑：从群体多样性方面考虑，群体越大越好，避免陷入局部最优；从计算效率方面考虑，群体规模越大将导致计算量的增加。应该根据实际问题确定种群的规模。产生初始化种群的方法通常有两种：一是完全随机的方法产生；二是根据先验知识设定一组必须满足的条件，然后根据这些条件生成初始样本。

（3）计算个体适应度：利用适应度函数计算各个个体的适应度大小。适应度函数（Fitness Function）的选取直接影响到遗传算法的收敛速度以及能否找到最优解，因为在进化搜索中基本不利用外部信息，仅以适应度函数为依据，利用种群每个个体的适应程度来指导搜索。

（4）进化计算：通过选择、交叉、变异，产生出代表新的解集的群体。选择（selection）：根据个体适应度大小，按照优胜劣汰的原则，淘汰不合理的个体；交叉（crossover）：编码的交叉重组，类似于染色体的交叉重组；变异（mutation）：编码按小概率扰动产生的变化，类似于基因突变。

（5）解码：末代种群中的最优个体经过解码实现从编码空间向解空间的映射，可以作为问题的近似最优解。这是整个遗传算法的最后一步，经过若干次的进化过程，种群中适应度最高的个体代表问题的最优解，但这个最优解还是一个由0和1组成的数字串，要将它转换成十进制才能供我们理解和使用。

4.遗传算法的参数设计原则

（1）种群的规模
种群不宜过大也不宜过小。种群规模的一个建议值为0-100。
（2）变异概率
变异概率也不宜过大或者过小。一般取值为0.0001-0.2。
（3）交换概率
不宜过大或者过小。一般取值 为0.4-0.99。
（4）进化代数
不宜过大或者过小。一般取值为100-500。
（5）种群初始化
初始种群的生成是随机的。在初始种群的赋予之前，尽量进行一个大概的区间估计，避免初始种群分布在远离最优解的编码空间，导致遗传算法的搜索范围受到限制。

5.代码实现

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

DNA_SIZE = 24
POP_SIZE = 200
CROSSOVER_RATE = 0.8
MUTATION_RATE = 0.005
N_GENERATIONS = 50
X_BOUND = [-3, 3]
Y_BOUND = [-3, 3]


def F(x, y):
    return 3 * (1 - x) ** 2 * np.exp(-(x ** 2) - (y + 1) ** 2) - 10 * (x / 5 - x ** 3 - y ** 5) * np.exp(
        -x ** 2 - y ** 2) - 1 / 3 ** np.exp(-(x + 1) ** 2 - y ** 2)


def plot_3d(ax):
    X = np.linspace(*X_BOUND, 100)
    Y = np.linspace(*Y_BOUND, 100)
    X, Y = np.meshgrid(X, Y)
    Z = F(X, Y)
    ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)
    ax.set_zlim(-10, 10)
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('z')
    plt.pause(3)
    plt.show()


def get_fitness(pop):
    x, y = translateDNA(pop)
    pred = F(x, y)
    return (pred - np.min(
        pred)) + 1e-3  # 减去最小的适应度是为了防止适应度出现负数，通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],最后在加上一个很小的数防止出现为0的适应度


def translateDNA(pop):  # pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目
    x_pop = pop[:, 1::2]  # 奇数列表示X
    y_pop = pop[:, ::2]  # 偶数列表示y

    # pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)
    x = x_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (X_BOUND[1] - X_BOUND[0]) + X_BOUND[0]
    y = y_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0]
    return x, y


def crossover_and_mutation(pop, CROSSOVER_RATE=0.8):
    new_pop = []
    for father in pop:  # 遍历种群中的每一个个体，将该个体作为父亲
        child = father  # 孩子先得到父亲的全部基因（这里我把一串二进制串的那些0，1称为基因）
        if np.random.rand() < CROSSOVER_RATE:  # 产生子代时不是必然发生交叉，而是以一定的概率发生交叉
            mother = pop[np.random.randint(POP_SIZE)]  # 再种群中选择另一个个体，并将该个体作为母亲
            cross_points = np.random.randint(low=0, high=DNA_SIZE * 2)  # 随机产生交叉的点
            child[cross_points:] = mother[cross_points:]  # 孩子得到位于交叉点后的母亲的基因
        mutation(child)  # 每个后代有一定的机率发生变异
        new_pop.append(child)

    return new_pop


def mutation(child, MUTATION_RATE=0.003):
    if np.random.rand() < MUTATION_RATE:  # 以MUTATION_RATE的概率进行变异
        mutate_point = np.random.randint(0, DNA_SIZE * 2)  # 随机产生一个实数，代表要变异基因的位置
        child[mutate_point] = child[mutate_point] ^ 1  # 将变异点的二进制为反转


def select(pop, fitness):  # nature selection wrt pop's fitness
    idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
                           p=(fitness) / (fitness.sum()))
    return pop[idx]


def print_info(pop):
    fitness = get_fitness(pop)
    max_fitness_index = np.argmax(fitness)
    print("max_fitness:", fitness[max_fitness_index])
    x, y = translateDNA(pop)
    print("最优的基因型：", pop[max_fitness_index])
    print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))


if __name__ == "__main__":
    fig = plt.figure()
    ax = Axes3D(fig)
    plt.ion()  # 将画图模式改为交互模式，程序遇到plt.show不会暂停，而是继续执行
    plot_3d(ax)

    pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 2))  # matrix (POP_SIZE, DNA_SIZE)
    for _ in range(N_GENERATIONS):  # 迭代N代
        x, y = translateDNA(pop)
        if 'sca' in locals():
            sca.remove()
        sca = ax.scatter(x, y, F(x, y), c='black', marker='o');
        plt.show();
        plt.pause(0.1)
        pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
        # F_values = F(translateDNA(pop)[0], translateDNA(pop)[1])#x, y --> Z matrix
        fitness = get_fitness(pop)
        pop = select(pop, fitness)  # 选择生成新的种群

    print_info(pop)
    plt.ioff()
    plot_3d(ax)