学习目标：

要学习二维随机变量的分布，我可能会遵循以下步骤：

了解基本概念：我会开始学习二维随机变量、联合概率密度函数、边缘概率密度函数、条件概率密度函数、期望值和方差等基本概念，以确保我对这些概念有一个牢固的理解。
学习分布类型：我会学习常见的二维随机变量分布类型，如二维正态分布、二项分布、泊松分布、指数分布、均匀分布等等，并且掌握如何应用这些分布类型。
掌握变换技巧：我会学习如何通过变换来分析二维随机变量分布，例如通过线性变换、逆变换、雅可比矩阵等技巧来转换随机变量，从而得到新的分布。
练习解决实际问题：我会通过练习题和实际案例来加强对二维随机变量分布的理解和应用能力，并且尝试使用统计软件来解决实际问题，例如R、Python等。
学习统计推断：我会学习如何进行参数估计和假设检验，并且掌握与二维随机变量分布有关的问题，例如联合分布的独立性检验等。
深入学习高级知识：最后，我会深入学习更高级的分布，例如卡方分布、t分布和F分布等，并且了解它们在统计学中的应用，以便在需要时可以更好地应用这些知识。

总的来说，学习二维随机变量分布需要耐心和实践。通过不断学习和练习，我相信我能够深入了解这个主题，并且在我的数学研究和实际应用中灵活运用它。

我的理解：

二维离散型随机变量函数的分布可以通过概率质量函数（PMF）来描述。假设 $X$ 和 $Y$ 是两个离散型随机变量，其取值分别为 x_1, x_2, 和 y_1, y_2, ，对于任意的 (x_i, y_j)，定义Z=g(X,Y) 为 X 和 Y 的函数，其中 g(\cdot) 是任意的实值函数。则 Z的概率质量函数可以表示为：

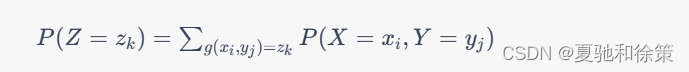
其中 z_k是 Z 可能的取值，即 g(x_i,y_j) 的所有可能取值，而 P(X=x_i, Y=y_j)则是 X 和 $Y$ 同时取到 x_i 和 y_j 的概率。我们可以通过计算 P(Z=z_k)来确定 Z的分布。

需要注意的是，当 g(\cdot)是单调函数时，可以通过变量替换的方式将 Z转化为另一个二维离散型随机变量，然后直接利用该变量的概率质量函数来计算 Z的分布。

另外，如果 X和 Y是独立的，那么 Z=g(X,Y) 也会是独立的，其概率质量函数可以通过 X 和 Y 的概率质量函数的卷积来计算。具体而言，设 p_X(x_i)和 p_Y(y_j)分别是 X 和 Y的概率质量函数，则 Z的概率质量函数可以表示为：

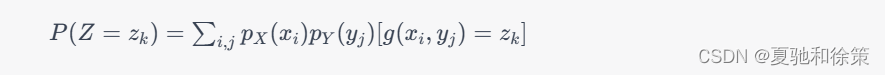
其中 [g(x_i,y_j)=z_k] 是指 g(x_i,y_j)等于 z_k 时取值为 1，否则取值为 0。

我的理解：

二维连续性随机变量可以用概率密度函数（PDF）来描述其分布。 PDF 是一个函数，可以用来描述两个随机变量取值的可能性。

对于一个二维连续性随机变量 (X,Y)，其概率密度函数为 f(x,y)。给定区域 D上的积分可以用来计算出 (X,Y)落在 D内的概率，即：

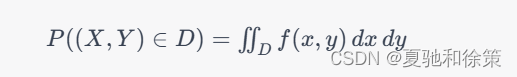
常见的二维连续性随机变量的分布包括：

均匀分布：在矩形区域 [a,b][c,d] 内的概率密度函数为：
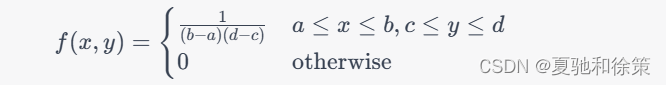
正态分布：具有以下概率密度函数的二维随机变量 (X,Y)是正态分布：

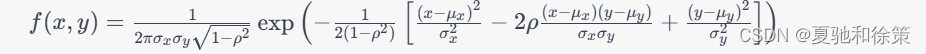
其中 \mu_x,\mu_y是均值，\sigma_x,\sigma_y 是标准差，\rho是相关系数。
指数分布：在第一象限内的概率密度函数为：

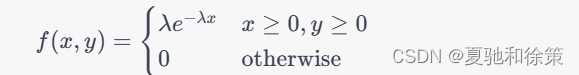
其中 \lambda是参数。
β分布：具有以下概率密度函数的二维随机变量 (X,Y) 是 β 分布：

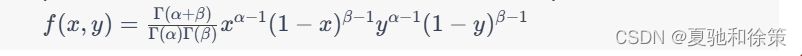
其中 alpha 和 \beta是参数，Gamma 是 gamma 函数。这个分布常用于模拟二项分布的概率分布。