感觉自己dp还不是很会（/(ㄒoㄒ)/~~

写dp题的步骤：①通过定义子问题，确定dp[ ] or dp[ ][ ] 表示的含义

②写出子问题的递归关系

③确定初始条件

题目：

思路：

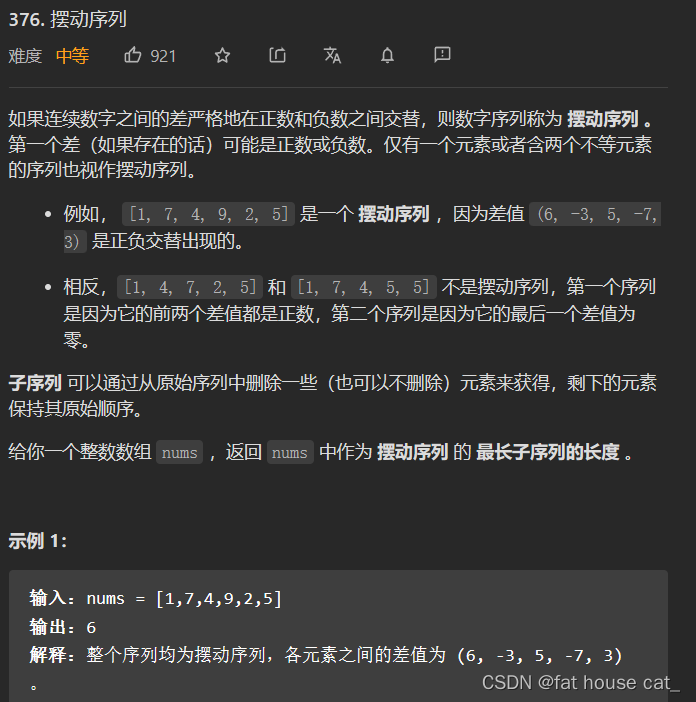
①确定dp的含义：dp[i]表示 到i位置，摆动序列的最长子序列的长度。

②现在我们要确定子问题的递归关系：dp[i]与dp[i-1]是什么关系呢？如果nums[i]>nums[i-1]，说明nums[i]要加入到以降序为结尾的摆动序列中。如果nums[i]<nums[i-1]，说明nums[i]要加入到以升序为结尾的摆动序列中。所以我们要确定dp[i-1]是具体以升序为结尾还是以降序为结尾的摆动序列。

因此，我们重新设置dp数组，用dp[i][0]表示 到i位置，以降序为结尾的摆动序列的最长子序列长度。用dp[i][1]表示 到i位置，以升序为结尾的摆动序列的最长子序列长度。

所以在确定了nums[i]与nums[i-1]的关系后，假如确定了nums[i]>nums[i-1]，那么dp[i][1]=dp[i-1][0]+1；dp[i][0]=dp[i-1][0]；

如果确定了nums[i]<nums[i-1]，那么dp[i][0]=dp[i-1][1]+1；dp[i][1]=dp[i-1][1]；

③初始化：dp[0][1]=dp[0][0]=1;

 代码：

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int[][] dp=new int[nums.length+1][2];
        dp[0][1]=dp[0][0]=1;
        for(int i=1;i<nums.length;i++){
            if(nums[i]>nums[i-1]){
                dp[i][1]=dp[i-1][0]+1;
                dp[i][0]=dp[i-1][0];
            }
            else if(nums[i]<nums[i-1]){
                dp[i][0]=dp[i-1][1]+1;
                dp[i][1]=dp[i-1][1];
            }
            else{
                dp[i][0]=dp[i-1][0];
                dp[i][1]=dp[i-1][1];
            }
        }
        return Math.max(dp[nums.length-1][0],dp[nums.length-1][1]);
    }
}

---

 题目2：

 思路：

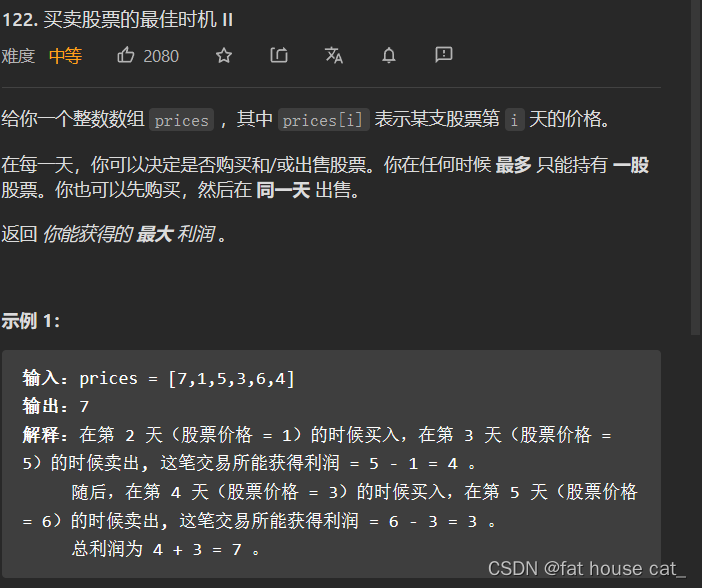
①确定dp数组

dp[i][0]表示第 i  天时未持股，获得的最大利润值。

dp[i][1]表示第 i 天时持股，获得的最大利润值。

②确定子问题的递归关系

dp[i][0]=max（dp[i-1][1]+prices[i]，dp[i-1][0]）；

dp[i][1]=max（dp[i-1][0]-prices[i]，dp[i-1][1]）；

③初始条件

dp[0][0]=0;

dp[0][1]=-prices[0];

代码：

class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp=new int[prices.length][2];
        dp[0][0]=0;
        dp[0][1]=-prices[0];
        for(int i=1;i<prices.length;i++){
            dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
            dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
        }
        return Math.max(dp[prices.length-1][0],dp[prices.length-1][1]);
    }
}