信息提取基础
MM
马卡洛夫链(Markov chain)是处理一类随机过程,这些过程包含最少量的内存,但实际上并不是无记忆的。下面,我们将处理离散随机变量和有限马尔可夫链。令 X1, X2, … , Xn, … 为随机变量序列,它们的值为同样有限字母表中的值 A = { 1, 2, … , c}。如果没有别的条件,那么贝叶斯公式适用:
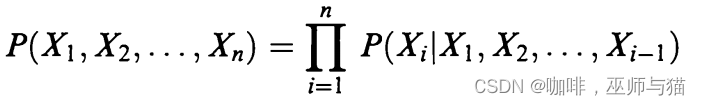
我们可以看出这是用联合概率密度公式推导来的:
P(A, B)=P(A|B) * P(B)=P(B|A) * P(A)
P(X1, X2)=P(X2|X1) * P(X1)
P(X1, X2, X3)=P(X3|X1,X2) * P(X1,X2)=P(X3|X1,X2) * P(X2|X1) * P(X1).
以此类推,就能得到公式。
然而,如果我们让这个公式成立:
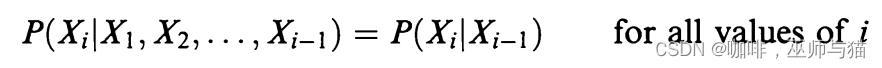
由此,随机变量形成马尔可夫链,作为结果马尔科夫链变为:
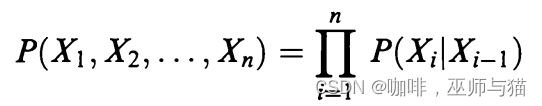
这样的一个随机过程就有最简单的记忆: 时间 i 的值仅取决于前一时间的值,而与发生的任何事情无关
在之前。
如果无视时间下标i的值,马尔科夫链是时不变(time invariant)的和齐次(homogeneous)的。
时不变:系统不随时间而变化,输出只由输入的值决定。
齐次:次数相等。
所以我们可以得到以下公式:
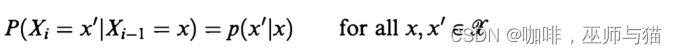
注:x, x’ 都属于之前提到的有限字母表集合中的值。
p(x’|x)被叫做转移函数(transition function),它可以被表示为一个 c x c 的矩阵。这个转移函数必须满足以下条件:
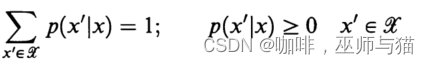
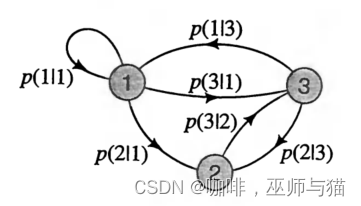
我们可以把Xi的值考虑为状态(states),这样马尔科夫链就可以被看作一个用转移函数p(x’|x)表示的在状态之间转移的有限状态过程(finite state process)。如果状态的数量不很大,那么链就可以用图表来表示,如下图所示,是一个状态空间大小为 c = 3的马尔科夫链。图中带有状态转移概率指的箭头表示状态的转换。没有表明的转移概率为0,如p(1|2) = p(2|2) = p(3|3)。
对于马尔科夫链的一站式记忆(只保存上一个状态作为输入)的限制其实是有欺骗性的,原则上马尔科夫链能够建模任意复杂程度的过程。比如下面这个例子,我们首先考虑一个记忆长度为k的过程,然后可以得到下面这个公式:
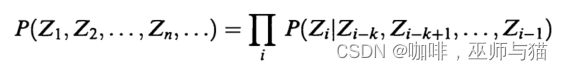
P
(
Z
1
,
Z
2
,
…
,
Z
n
,
…
)
=
∏
i
P
(
Z
i
∣
Z
i
−
k
,
Z
i
−
k
+
1
,
…
,
Z
i
−
1
)
P(Z_1, Z_2, \ldots, Z_n, \ldots) = \prod_{i} P(Z_i \mid Z_{i-k}, Z_{i-k+1}, \ldots, Z_{i-1})
P(Z1,Z2,…,Zn,…)=i∏P(Zi∣Zi−k,Zi−k+1,…,Zi−1)
我们可以看出这个过程的当前状态是由上k个状态决定的,现在我们来定义一个新的变量X,让它等于k个Z状态。我们就可以得到下面的公式:
这样我们就可以得到,Zi+1状态可以由Xi状态作为输入得到,这就又变回马尔科夫链了。
HMM
HMM和MM的不同: 隐式马尔科夫链可以在不改变马尔科夫链基本结构的前提下允许随机过程拥有更多的自由度。
隐式马尔科夫链的原理:首先让链的状态产生观察数据,然后隐藏状态序列本身。
因此,我们可以定义:
- 一个可以观察到的输出集合:y = {0,1,…,b-1}
- 一个状态空间 S = {1,2,…,c} 带有一个单独的不重复初始状态s0。
- 一个状态之间的概率分布转移p(s’|s)。
- 一个和状态从s转移到状态s’关联的输出观察状态概率分布q(y|s,s’)。
这样,观察到一个HMM的输出序列 y1, y2, … , yk的可能性为以下公式:
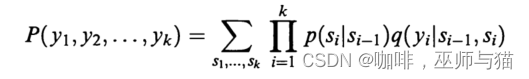
P ( y 1 , y 2 , … , y k ) = ∑ s 1 , . . . , s k ∏ i = 1 k p ( s i ∣ s i − 1 ) q ( y i ∣ s i − 1 , s i ) P(y_1, y_2, \ldots, y_k) = \sum_{s1,...,sk}\prod_{i=1}^{k} p(s_i \mid s_{i-1}) q(y_i \mid s_{i-1}, s_i) P(y1,y2,…,yk)=s1,...,sk∑i=1∏kp(si∣si−1)q(yi∣si−1,si)
P ( O , s 1 , s 2 , . . . , s T ∣ λ ) = π s 1 ⋅ B s 1 ( O 1 ) ⋅ ∏ t = 2 T A s t − 1 , s t ⋅ B s t ( O t ) P(O, s_1, s_2, ..., s_T | \lambda) = \pi_{s_1} \cdot B_{s_1}(O_1) \cdot \prod_{t=2}^T A_{s_{t-1}, s_t} \cdot B_{s_t}(O_t) P(O,s1,s2,...,sT∣λ)=πs1⋅Bs1(O1)⋅t=2∏TAst−1,st⋅Bst(Ot)
下面我们来解析一下这个公式:
首先,
p
(
s
i
∣
s
i
−
1
)
p(s_i \mid s_{i-1})
p(si∣si−1) 代表的是状态
s
i
−
1
s_{i-1}
si−1 到状态
s
i
s_i
si 的可能性,
q
(
y
i
∣
s
i
−
1
,
s
i
)
q(y_i \mid s_{i-1}, s_i)
q(yi∣si−1,si) 代表的是观察状态概率分布中从状态
s
i
−
1
s_{i-1}
si−1 到状态
s
i
s_i
si 发生的情况下, 观察状态
y
i
y_i
yi 发生的可能性。所以,
∏
i
=
1
k
p
(
s
i
∣
s
i
−
1
)
q
(
y
i
∣
s
i
−
1
,
s
i
)
\prod_{i=1}^{k} p(s_i \mid s_{i-1}) q(y_i \mid s_{i-1}, s_i)
∏i=1kp(si∣si−1)q(yi∣si−1,si) 就表示一条隐藏的状态序列发生后,得到观察序列
y
1
,
y
2
,
…
,
y
k
y_1, y_2, \ldots, y_k
y1,y2,…,yk的可能性是多少,能得到这种观察状态序列的隐藏状态序列可能不止一种,所以把所有可能的状态序列加起来,就得到了当我们拥有这些隐藏状态时生成这个观察序列的可能性。
如果我们看下面这个公式,可能会更清晰一些:
让 O O O 成为长度为 T T T 的观测序列, Q Q Q 成为长度为 T T T 的隐藏状态序列。观测序列和隐藏状态序列的联合概率可以表示为:
P ( O , Q ∣ θ ) = π q 1 b q 1 ( O 1 ) ∏ t = 2 T a q t − 1 , q t b q t ( O t ) P(O, Q | \theta) = \pi_{q_1} b_{q_1}(O_1) \prod_{t=2}^T a_{q_{t-1}, q_t} b_{q_t}(O_t) P(O,Q∣θ)=πq1bq1(O1)t=2∏Taqt−1,qtbqt(Ot)
其中, θ = ( A , B , π ) \theta=(A, B, \pi) θ=(A,B,π) 为HMM参数集, q t q_t qt 是时间 t t t 的隐藏状态, π q 1 \pi_{q_1} πq1 是开始于隐藏状态 q 1 q_1 q1 的初始概率, a q t − 1 , q t a_{q_{t-1}, q_t} aqt−1,qt 是从隐藏状态 q t − 1 q_{t-1} qt−1 转移至隐藏状态 q t q_t qt 的转移概率, b q t ( O t ) b_{q_t}(O_t) bqt(Ot) 是在给定隐藏状态 q t q_t qt 的情况下观测到 O t O_t Ot 的观测概率。
给定 HMM 模型 θ \theta θ,观测序列 O O O 的概率可以通过对所有可能的隐藏状态序列进行边缘化计算得到:
P ( O ∣ θ ) = ∑ Q P ( O , Q ∣ θ ) P(O | \theta) = \sum_{Q} P(O, Q | \theta) P(O∣θ)=Q∑P(O,Q∣θ)
其中,求和是对所有可能的隐藏状态序列 Q Q Q 进行的。
如果换个思路,将HMM看作是在多个状态对之间的多个转换,每个转换都输出一个不同的观察状态,一个状态转换为其他状态的总可能性为1,就会方便很多。
下面,我们用格架(trellis)图来举个例子:
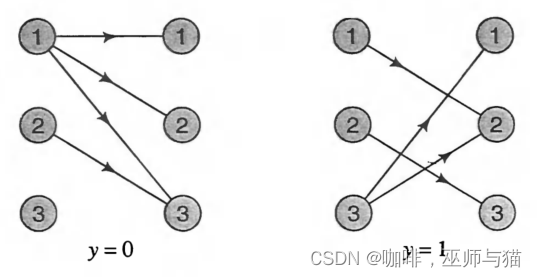
从图上我们可以看出,状态1,转变为状态1,2,3时,可能会输出观察状态0,从状态1转为状态2时,可能会输出观察状态1。
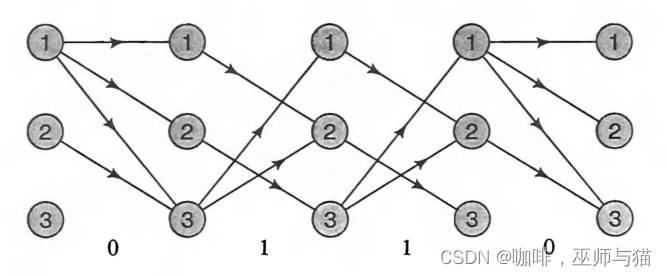
所以如果我们要输出观察状态序列0110,就会有下图这些可能的路径状态转换序列。
维特比(Viterbi)算法
当我们已知观察序列,想要找到最大可能的路径时会使用这个算法。
首先根据联合概率密度公式可推出:
P ( s 1 , s 2 , … , s k ∣ Y 1 , Y 2 , … , Y k , s 0 ) = P ( s 1 , s 2 , … , s k , Y 1 , Y 2 , … , Y k ∣ s 0 ) P ( Y 1 , Y 2 , … , Y k ∣ s 0 ) P( s_1, s_2, \dots, s_k\mid Y_1, Y_2, \dots, Y_k, s_0) = \frac{P(s_1, s_2, \dots, s_k, Y_1, Y_2, \dots, Y_k \mid s_0)} {P( Y_1, Y_2, \dots, Y_k \mid s_0)} P(s1,s2,…,sk∣Y1,Y2,…,Yk,s0)=P(Y1,Y2,…,Yk∣s0)P(s1,s2,…,sk,Y1,Y2,…,Yk∣s0)
当我们想找到最大可能的路径时,我们需要找到一个隐藏状态序列
s
1
,
s
2
,
…
,
s
k
s_1, s_2, \dots, s_k
s1,s2,…,sk来实现最大化分子。
这是我们需要求出每一个时间点的所有状态的可能性,一直算到最后一个时间,得到所有状态的可能性后选择其中最大的状态,向前反推出每个时间点选择的状态,最后就可以得出可能性最大的路径。
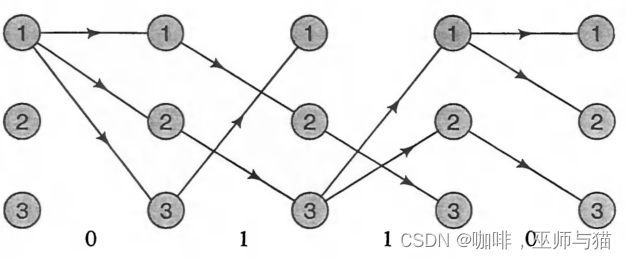
例如上面观察序列为0110的图像,加入我们算到最后一个时间发现状态3的可能性最大。我们就可以反推出最大可能性的路径为12323。
空(Null)转移
空转移代表状态发生了变化但是却没有输出观察数据,一般用虚线表示。
下图是一个空转移的例子:
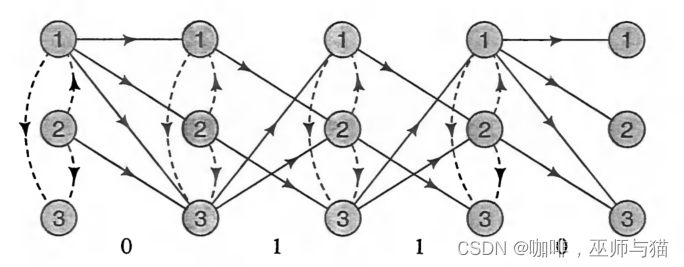
令 q(s’ls) 为从 s 到 s’ 的空转移的概率。让r(y, s’ls) 是从 s 到 s’ 的(非空)转换产生输出 y 的概率:
∑
y
,
s
′
r
(
y
,
s
∣
s
′
)
+
∑
s
′
q
(
s
′
∣
s
)
=
1
\sum_{y, s'}r(y, s \mid s') +\sum_{s'}q(s' \mid s) = 1
y,s′∑r(y,s∣s′)+s′∑q(s′∣s)=1
HMM的三种情况
- 评估:给定HMM模型(初始状态概率,状态转移矩阵,观测概率矩阵),求某一个观察数据序列的概率。
解答算法:向前算法,向后算法。
举例:
有这样一个HMM模型如下图所示:
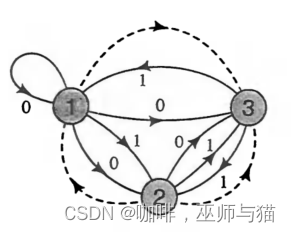
可以看出HMM模型有三个状态S = {1, 2, 3},有两个输出数据Y = {0, 1}。
现在给出下面的条件:输出观察数据的转移矩阵和空转移矩阵分别为:
p ( s ′ ∣ s ) = [ 1 2 1 6 1 6 0 0 1 3 3 4 1 4 0 ] , q ( s ′ ∣ s ) = [ 0 0 1 6 1 3 0 1 3 0 0 0 ] , s , s ′ ∈ S p(s' | s) = \begin{bmatrix} \frac{1}{2} & \frac{1}{6} & \frac{1}{6} \\ 0 & 0 & \frac{1}{3} \\ \frac{3}{4} & \frac{1}{4} & 0 \end{bmatrix}, \qquad q(s' | s) = \begin{bmatrix} 0 & 0 & \frac{1}{6} \\ \frac{1}{3} & 0 & \frac{1}{3} \\ 0 & 0 & 0 \end{bmatrix}, \qquad s, s' \in S p(s′∣s)= 210436104161310 ,q(s′∣s)= 031000061310 ,s,s′∈S
输出观察数据的矩阵转移概率为:
q ( 0 ∣ s → s ′ ) = [ 1 1 2 1 0 0 1 3 0 0 0 ] , q ( 1 ∣ s → s ′ ) = [ 0 1 2 0 1 1 2 3 1 1 1 ] , q(0 | s \rightarrow s') = \begin{bmatrix} 1 & \frac{1}{2} & 1 \\ 0 & 0 & \frac{1}{3} \\ 0 & 0 & 0 \end{bmatrix}, \qquad q(1 | s \rightarrow s') = \begin{bmatrix} 0 & \frac{1}{2} &0 \\ 1 & 1 & \frac{2}{3} \\ 1 & 1 & 1 \end{bmatrix}, q(0∣s→s′)= 10021001310 ,q(1∣s→s′)= 01121110321 ,
注意: q ( 1 ∣ s → s ′ ) q(1 | s \rightarrow s') q(1∣s→s′)就是 1 − q ( 0 ∣ s → s ′ ) 1-q(0 | s \rightarrow s') 1−q(0∣s→s′)。初始状态为 s 0 = 1 s_0=1 s0=1,也就是 π = { 1 , 0 , 0 } \pi=\{1, 0, 0\} π={1,0,0}
使用前向算法计算观察序列为0110的可能性。
首先可以画出观察序列的状态格架图:
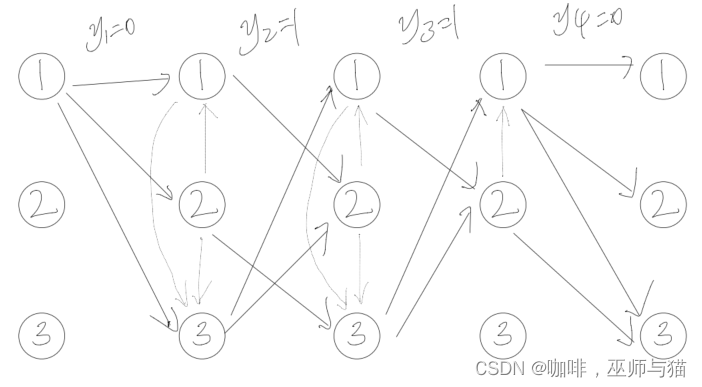
然后可以开始计算:
由于空转移是在状态转移的开始阶段发生的,所以要先计算空转移,之后才是观察数据的状态转移。我们使用r(y, s’|s)表示非空输出的状态转移概率,q(s’|s)表示空转移的概率。
初始状态:
α
0
(
1
)
=
1
\alpha_0(1)=1
α0(1)=1
第一次状态转移:
α
1
(
1
)
=
α
0
(
1
)
r
(
0
,
1
∣
1
)
=
α
0
(
1
)
p
(
1
∣
1
)
q
(
0
∣
1
→
1
)
=
1
×
1
2
×
1
=
1
2
\alpha_1(1)=\alpha_0(1)r(0, 1|1)=\alpha_0(1)p(1|1)q(0 | 1 \rightarrow 1)=1\times\frac{1}{2}\times1=\frac{1}{2}
α1(1)=α0(1)r(0,1∣1)=α0(1)p(1∣1)q(0∣1→1)=1×21×1=21
α
1
(
2
)
=
α
0
(
1
)
r
(
0
,
2
∣
1
)
=
α
0
(
1
)
p
(
2
∣
1
)
q
(
0
∣
1
→
2
)
=
1
×
1
6
×
1
2
=
1
12
\alpha_1(2)=\alpha_0(1)r(0, 2|1)=\alpha_0(1)p(2|1)q(0 | 1 \rightarrow 2)=1\times\frac{1}{6}\times\frac{1}{2}=\frac{1}{12}
α1(2)=α0(1)r(0,2∣1)=α0(1)p(2∣1)q(0∣1→2)=1×61×21=121
α
1
(
3
)
=
α
0
(
1
)
r
(
0
,
3
∣
1
)
=
α
0
(
1
)
p
(
3
∣
1
)
q
(
0
∣
1
→
3
)
=
1
×
1
6
×
1
=
1
6
\alpha_1(3)=\alpha_0(1)r(0, 3|1)=\alpha_0(1)p(3|1)q(0 | 1 \rightarrow 3)=1\times\frac{1}{6}\times1=\frac{1}{6}
α1(3)=α0(1)r(0,3∣1)=α0(1)p(3∣1)q(0∣1→3)=1×61×1=61
第二次状态转移:
先计算空转移:
α
1
(
2
)
=
α
1
(
2
)
=
1
12
\alpha_1(2)=\alpha_1(2)=\frac{1}{12}
α1(2)=α1(2)=121 (没有空转移从别的状态变为状态2)。
α
1
(
1
)
=
α
1
(
1
)
+
α
1
(
2
)
q
(
1
∣
2
)
=
1
2
+
1
12
×
1
3
=
19
36
\alpha_1(1)=\alpha_1(1)+\alpha_1(2)q(1|2) =\frac{1}{2}+\frac{1}{12}\times\frac{1}{3}=\frac{19}{36}
α1(1)=α1(1)+α1(2)q(1∣2)=21+121×31=3619 (空转移从状态2转变为状态1)
α
1
(
3
)
=
α
1
(
3
)
+
α
1
(
1
)
q
(
3
∣
1
)
+
α
1
(
2
)
q
(
3
∣
2
)
=
1
6
+
19
36
×
1
6
+
1
12
×
1
3
=
61
216
\alpha_1(3)=\alpha_1(3)+\alpha_1(1)q(3|1)+\alpha_1(2)q(3|2) =\frac{1}{6}+\frac{19}{36}\times\frac{1}{6}+\frac{1}{12}\times\frac{1}{3}=\frac{61}{216}
α1(3)=α1(3)+α1(1)q(3∣1)+α1(2)q(3∣2)=61+3619×61+121×31=21661
观测数据转移:
α
2
(
1
)
=
α
1
(
3
)
r
(
1
,
1
∣
3
)
=
61
216
×
3
4
×
1
=
0.212
\alpha_2(1)=\alpha_1(3)r(1, 1|3)=\frac{61}{216}\times\frac{3}{4}\times1=0.212
α2(1)=α1(3)r(1,1∣3)=21661×43×1=0.212
α
2
(
2
)
=
α
1
(
1
)
r
(
1
,
2
∣
1
)
+
α
1
(
3
)
r
(
1
,
2
∣
3
)
=
19
36
×
1
6
×
1
2
+
61
216
×
1
4
×
1
=
0.115
\alpha_2(2)=\alpha_1(1)r(1, 2|1)+\alpha_1(3)r(1, 2|3)=\frac{19}{36}\times\frac{1}{6}\times\frac{1}{2}+\frac{61}{216}\times\frac{1}{4}\times1=0.115
α2(2)=α1(1)r(1,2∣1)+α1(3)r(1,2∣3)=3619×61×21+21661×41×1=0.115
α
2
(
3
)
=
α
1
(
2
)
r
(
1
,
3
∣
2
)
=
1
12
×
1
3
×
2
3
=
0.019
\alpha_2(3)=\alpha_1(2)r(1, 3|2)=\frac{1}{12}\times\frac{1}{3}\times\frac{2}{3}=0.019
α2(3)=α1(2)r(1,3∣2)=121×31×32=0.019
第三次状态转移:
先计算空转移:
α
2
(
2
)
=
α
2
(
2
)
=
0.115
\alpha_2(2)=\alpha_2(2)=0.115
α2(2)=α2(2)=0.115 (没有空转移从别的状态变为状态2)。
α
2
(
1
)
=
α
2
(
1
)
+
α
2
(
2
)
q
(
1
∣
2
)
=
0.212
+
0.115
×
1
3
=
0.250
\alpha_2(1)=\alpha_2(1)+\alpha_2(2)q(1|2) =0.212+0.115\times\frac{1}{3}=0.250
α2(1)=α2(1)+α2(2)q(1∣2)=0.212+0.115×31=0.250
α
2
(
3
)
=
α
2
(
3
)
+
α
2
(
1
)
q
(
3
∣
1
)
+
α
2
(
2
)
q
(
3
∣
2
)
=
0.019
+
0.250
×
1
6
+
0.115
×
1
3
=
0.099
\alpha_2(3)=\alpha_2(3)+\alpha_2(1)q(3|1)+\alpha_2(2)q(3|2) =0.019+0.250\times\frac{1}{6}+0.115\times\frac{1}{3}=0.099
α2(3)=α2(3)+α2(1)q(3∣1)+α2(2)q(3∣2)=0.019+0.250×61+0.115×31=0.099
观测数据转移:
α
3
(
1
)
=
α
2
(
3
)
r
(
1
,
1
∣
3
)
=
0.099
×
3
4
×
1
=
0.074
\alpha_3(1)=\alpha_2(3)r(1, 1|3)=0.099\times\frac{3}{4}\times1=0.074
α3(1)=α2(3)r(1,1∣3)=0.099×43×1=0.074
α
3
(
2
)
=
α
2
(
1
)
r
(
1
,
2
∣
1
)
+
α
2
(
3
)
r
(
1
,
2
∣
3
)
=
0.250
×
1
6
×
1
2
+
0.099
×
1
4
×
1
=
0.046
\alpha_3(2)=\alpha_2(1)r(1, 2|1)+\alpha_2(3)r(1, 2|3)=0.250\times\frac{1}{6}\times\frac{1}{2}+0.099\times\frac{1}{4}\times1=0.046
α3(2)=α2(1)r(1,2∣1)+α2(3)r(1,2∣3)=0.250×61×21+0.099×41×1=0.046
注:因为在下一次的状态转移中
p
(
0
∣
3
→
1
)
,
p
(
0
∣
3
→
2
)
,
p
(
0
∣
3
→
3
)
p(0 | 3 \rightarrow 1), p(0 | 3 \rightarrow 2), p(0 | 3 \rightarrow 3)
p(0∣3→1),p(0∣3→2),p(0∣3→3)的值都为0,所以就不计算
α
3
(
3
)
\alpha_3(3)
α3(3)的概率。
第四次状态转移:
先计算空转移:
α
3
(
2
)
=
α
3
(
2
)
=
0.046
\alpha_3(2)=\alpha_3(2)=0.046
α3(2)=α3(2)=0.046 (没有空转移从别的状态变为状态2)。
α
3
(
1
)
=
α
3
(
1
)
+
α
3
(
2
)
q
(
1
∣
2
)
=
0.074
+
0.046
×
1
3
=
0.089
\alpha_3(1)=\alpha_3(1)+\alpha_3(2)q(1|2) =0.074+0.046\times\frac{1}{3}=0.089
α3(1)=α3(1)+α3(2)q(1∣2)=0.074+0.046×31=0.089
观测数据转移:
α
4
(
1
)
=
α
3
(
1
)
r
(
0
,
1
∣
1
)
=
0.089
×
1
2
×
1
=
0.045
\alpha_4(1)=\alpha_3(1)r(0, 1|1)=0.089\times\frac{1}{2}\times1=0.045
α4(1)=α3(1)r(0,1∣1)=0.089×21×1=0.045
α
4
(
2
)
=
α
3
(
1
)
r
(
0
,
2
∣
1
)
=
0.089
×
1
6
×
1
2
=
0.007
\alpha_4(2)=\alpha_3(1)r(0, 2|1)=0.089\times\frac{1}{6}\times\frac{1}{2}=0.007
α4(2)=α3(1)r(0,2∣1)=0.089×61×21=0.007
α
4
(
3
)
=
α
3
(
1
)
r
(
0
,
3
∣
1
)
+
α
3
(
2
)
r
(
0
,
3
∣
2
)
=
0.089
×
1
6
×
1
+
0.046
×
1
3
×
1
3
=
0.020
\alpha_4(3)=\alpha_3(1)r(0, 3|1)+\alpha_3(2)r(0, 3|2)=0.089\times\frac{1}{6}\times1+0.046\times\frac{1}{3}\times\frac{1}{3}=0.020
α4(3)=α3(1)r(0,3∣1)+α3(2)r(0,3∣2)=0.089×61×1+0.046×31×31=0.020
所以我们可以得到观察序列为0110时,边际概率为:
P
(
y
1
y
2
y
3
y
4
=
0110
∣
s
0
=
1
)
=
∑
s
α
4
=
α
4
(
1
)
+
α
4
(
2
)
+
α
4
(
3
)
=
0.045
+
0.007
+
0.020
=
0.072
P(y_1y_2y_3y_4=0110|s_0=1)=\sum_{s}\alpha_4=\alpha_4(1)+\alpha_4(2)+\alpha_4(3)=0.045+0.007+0.020=0.072
P(y1y2y3y4=0110∣s0=1)=∑sα4=α4(1)+α4(2)+α4(3)=0.045+0.007+0.020=0.072
注:边际概率为P(A),只和一个变量有关系,所以为所有状态能得到观察数据序列0110的概率之和。根据联合概率密度公式,条件概率,联合概率,和边际概率的关系为:
P(A, B)=P(A|B) * P(B)
- 解码:给定HMM模型(初始状态概率,状态转移矩阵,观测概率矩阵),和某一个观察序列,推测最大可能的状态转移路径。
解答算法:维特比(Viterbi)算法
还是上一个例子的HMM模型,观察到一个观察序列为0110,求可能性最大的状态转移路径。
γ i ( s i ) = max s 1 , s 2 , … , s i − 1 P ( s 1 , s 2 , … , s i , y 1 , y 2 , … , y i ∣ s 0 ) = max s i − 1 p ( y i , s i ∣ s i − 1 ) max s 1 , s 2 , … , s i − 2 P ( s 1 , s 2 , … , s i − 1 , y 1 , y 2 , … , y i ∣ s 0 ) = max s i − 1 p ( y i , s i ∣ s i − 1 ) γ i − 1 ( s i − 1 ) \gamma_i(s_i) = \max_{s_1, s_2, \dots, s_{i-1}}P(s_1, s_2, \dots, s_i, y_1, y_2, \dots, y_i \mid s_0) \\ =\max_{s_{i-1}}p( y_i, s_i \mid s_{i-1}) \max_{s_1, s_2, \dots, s_{i-2}}P(s_1, s_2, \dots, s_{i-1}, y_1, y_2, \dots, y_i \mid s_0) \\ = \max_{s_{i-1}}p( y_i, s_i \mid s_{i-1})\gamma_{i-1}(s_{i-1}) γi(si)=maxs1,s2,…,si−1P(s1,s2,…,si,y1,y2,…,yi∣s0)=maxsi−1p(yi,si∣si−1)maxs1,s2,…,si−2P(s1,s2,…,si−1,y1,y2,…,yi∣s0)=maxsi−1p(yi,si∣si−1)γi−1(si−1)
所以, γ i ( s ) \gamma_i(s) γi(s)指代的就是每次转移的最大可能性的状态的概率。
初始状态:
γ 0 ( 1 ) = 1 \gamma_0(1)=1 γ0(1)=1
注:(r(0, 2|1) = q(0|1, 2)p(2|1))
求第一层所有状态的概率:
γ 1 ( 2 ) = γ 0 ( 1 ) r ( 0 , 2 ∣ 1 ) = 1 12 \gamma_1(2)=\gamma_0(1)r(0, 2|1)=\frac{1}{12} γ1(2)=γ0(1)r(0,2∣1)=121
γ 1 ( 1 ) = max { γ 0 ( 1 ) r ( 0 , 1 ∣ 1 ) , γ 1 ( 2 ) q ( 1 ∣ 2 ) } = 1 2 \gamma_1(1)=\max\{\gamma_0(1)r(0, 1|1), \gamma_1(2)q(1|2)\}=\frac{1}{2} γ1(1)=max{γ0(1)r(0,1∣1),γ1(2)q(1∣2)}=21
γ 1 ( 3 ) = max { γ 0 ( 1 ) r ( 0 , 3 ∣ 1 ) , γ 1 ( 2 ) q ( 3 ∣ 2 ) , γ 1 ( 1 ) q ( 3 ∣ 1 ) } = 1 6 \gamma_1(3)=\max\{\gamma_0(1)r(0, 3|1), \gamma_1(2)q(3|2), \gamma_1(1)q(3|1)\}=\frac{1}{6} γ1(3)=max{γ0(1)r(0,3∣1),γ1(2)q(3∣2),γ1(1)q(3∣1)}=61
求第二层所有状态的概率:
γ 2 ( 2 ) = max { γ 1 ( 1 ) r ( 1 , 2 ∣ 1 ) , γ 1 ( 3 ) r ( 1 , 2 ∣ 3 ) } = 1 24 \gamma_2(2)=\max\{\gamma_1(1)r(1, 2|1), \gamma_1(3)r(1, 2|3)\}=\frac{1}{24} γ2(2)=max{γ1(1)r(1,2∣1),γ1(3)r(1,2∣3)}=241
γ 2 ( 1 ) = max { γ 1 ( 3 ) r ( 1 , 1 ∣ 3 ) , γ 2 ( 2 ) q ( 1 ∣ 2 ) } = 1 8 \gamma_2(1)=\max\{\gamma_1(3)r(1, 1|3), \gamma_2(2)q(1|2)\}=\frac{1}{8} γ2(1)=max{γ1(3)r(1,1∣3),γ2(2)q(1∣2)}=81
γ 2 ( 3 ) = max { γ 1 ( 2 ) r ( 1 , 3 ∣ 2 ) , γ 2 ( 2 ) q ( 3 ∣ 2 ) , γ 2 ( 1 ) q ( 3 ∣ 1 ) } = 1 48 \gamma_2(3)=\max\{\gamma_1(2)r(1, 3|2), \gamma_2(2)q(3|2), \gamma_2(1)q(3|1)\}=\frac{1}{48} γ2(3)=max{γ1(2)r(1,3∣2),γ2(2)q(3∣2),γ2(1)q(3∣1)}=481
求第三层所有状态的概率:
γ 3 ( 2 ) = max { γ 2 ( 1 ) r ( 1 , 2 ∣ 1 ) , γ 2 ( 3 ) r ( 1 , 2 ∣ 3 ) } = 1 96 \gamma_3(2)=\max\{\gamma_2(1)r(1, 2|1), \gamma_2(3)r(1, 2|3)\}=\frac{1}{96} γ3(2)=max{γ2(1)r(1,2∣1),γ2(3)r(1,2∣3)}=961
γ 3 ( 1 ) = max { γ 2 ( 3 ) r ( 1 , 1 ∣ 3 ) , γ 3 ( 2 ) q ( 1 ∣ 2 ) } = 1 64 \gamma_3(1)=\max\{\gamma_2(3)r(1, 1|3), \gamma_3(2)q(1|2)\}=\frac{1}{64} γ3(1)=max{γ2(3)r(1,1∣3),γ3(2)q(1∣2)}=641
求最后一层所有状态的概率:
γ 4 ( 2 ) = γ 3 ( 1 ) r ( 0 , 2 ∣ 1 ) = 1 768 \gamma_4(2)=\gamma_3(1)r(0, 2|1)=\frac{1}{768} γ4(2)=γ3(1)r(0,2∣1)=7681
γ 4 ( 1 ) = γ 3 ( 1 ) r ( 0 , 1 ∣ 1 ) = 1 128 \gamma_4(1)=\gamma_3(1)r(0, 1|1)=\frac{1}{128} γ4(1)=γ3(1)r(0,1∣1)=1281
γ 4 ( 3 ) = max { γ 3 ( 1 ) r ( 0 , 3 ∣ 1 ) , γ 3 ( 2 ) r ( 0 , 3 ∣ 2 ) } = 1 384 \gamma_4(3)=\max\{\gamma_3(1)r(0, 3|1), \gamma_3(2)r(0, 3|2)\}=\frac{1}{384} γ4(3)=max{γ3(1)r(0,3∣1),γ3(2)r(0,3∣2)}=3841
第四层可能性最大的是状态1的 1 128 \frac{1}{128} 1281所以由此可以向前推出最有可能的路径是 1 → 3 → 1 → 3 ( 发生空转移 ) → 1 → 1 1\rightarrow3\rightarrow1\rightarrow3(发生空转移) \rightarrow1\rightarrow1 1→3→1→3(发生空转移)→1→1
注:时间点为2的时候的那一列, 因为空转移从1到3的概率大于了其他状态转移概率,所以发生了从1到3的空转移。 - 学习问题
到目前为止,我们解决问题的时候都给出了HMM的参数。但是在大部分情况下,我们并没有转换和观察的概率。我们想要做的是构建一个模型,用这个模型来解释和这个模型类型相同的未来数据。但是没有一种好的方法来估计HMM的转换结构和统计参数。所以只能利用直觉来设计HMM结构和估计参数值。这就是最大可能性的方法,即极大似然法:
设 P λ ( Y ) {P_\lambda(Y)} Pλ(Y)为由 λ {\lambda} λ参数定义的HMM产生观察序列输出 Y = y 1 , y 2 , … , y k {Y=y_1, y_2, \dots, y_k} Y=y1,y2,…,yk的可能性,则可以得到:
λ ^ = a r g m a x λ P λ ( Y ) {\hat{\lambda}=arg max_\lambda P_\lambda(Y)} λ^=argmaxλPλ(Y)
即找到参数 λ \lambda λ使得模型HMM输出观察序列 Y = y 1 , y 2 , … , y k {Y=y_1, y_2, \dots, y_k} Y=y1,y2,…,yk的可能性最大。
其中Y为训练数据,最好让训练数据足够具有代表性,这样得到的参数 λ \lambda λ对于未来的数据也能处理的比较让人满意。
注:最大似然方法会给人一个错误的暗示,那就是训练观察数据Y是由带有参数 λ \lambda λ的HMM产生的。实际上我们并不知道Y是由哪个HMM模型产生的,我们只是用给出的训练数据Y去尽可能的估计出一个HMM。
为了方便理解最大似然方法,我们作出以下假设:
任何一对状态s和s’之间的转移t最多只有一个输出, L(t)=s, R(t)=s’, 和最多一个空转移t’, L(t’)=s,R(t’)=s’。
我们仍然使用简化符号:
q ( y ∣ t ) = q ( y ∣ s , s ′ ) q(y|t)=q(y|s, s') q(y∣t)=q(y∣s,s′)
(注: L(t)=s为转移左边的状态, R(t)=s’为转移右边的状态)
我们先看一个例子:
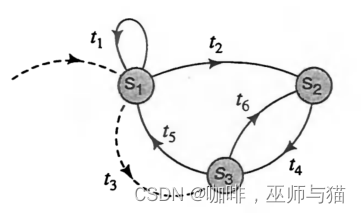
我们可以看出图中一共有3个状态和6个转移,包含一个t3空转移。假设这个HMM可以输出二进制的观察序列。并且从状态 s 1 s_1 s1开始,即 s 0 = 1 s_0=1 s0=1。
我们想要估计具体的转移矩阵概率 p ( t i ) p(t_i) p(ti)和输出矩阵概率 q ( y ∣ t i ) q(y|t_i) q(y∣ti)。我们还不知道这些参数,但我们可以得出:
p ( t 1 ) + p ( t 2 ) + p ( t 3 ) = 1 ; p ( t 5 ) + p ( t 6 ) = 1 p(t_1)+p(t_2)+p(t_3)=1; p(t_5)+p(t_6)=1 p(t1)+p(t2)+p(t3)=1;p(t5)+p(t6)=1
注: 此处还有一个知识点,即如果HMM模型有观察序列 Y = y 1 , y 2 , … , y k {Y=y_1, y_2, \dots, y_k} Y=y1,y2,…,yk,隐藏状态序列: T = t 1 , t 2 , … , t m {T=t_1, t_2, \dots, t_m} T=t1,t2,…,tm,则 m > = k m>=k m>=k,因为m还有空转移。
在这个例子里,我们假设输出序列为 Y = y 1 , y 2 , y 3 , y 4 {Y=y_1, y_2, y_3, y_4} Y=y1,y2,y3,y4,并且图中加上上标,代表来源为第几阶段。
接下来我们定义指标函数:
I i ( t ) = { 1 如果一个状态的状态转移序列的集合 T 中存在一个在第 i 个阶段的转移 t 0 其他情况 I_i(t) = \begin{cases} 1 & \text{如果一个状态的状态转移序列的集合 } T \text{ 中存在一个在第 } i \text{ 个阶段的转移 } t \\ 0 & \text{其他情况} \end{cases} Ii(t)={10如果一个状态的状态转移序列的集合 T 中存在一个在第 i 个阶段的转移 t其他情况
然后我们可以画出下面的格架图:
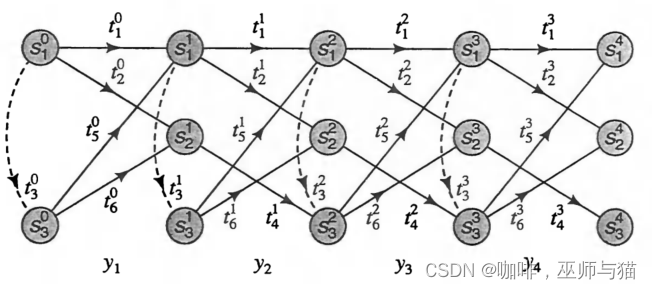
所以我们可以得到下面的公式:
c ( t ) = ∑ i = 0 k − 1 I i ( t ) c(t)=\sum_{i=0}^{k-1}I_i(t) c(t)=∑i=0k−1Ii(t)
对于非空转移t,我们可以得到:
c ( y , t ) = ∑ i = 0 k − 1 I i ( t ) δ ( y i + 1 , y ) c(y, t)=\sum_{i=0}^{k-1}I_i(t)\delta(y_{i+1}, y) c(y,t)=∑i=0k−1Ii(t)δ(yi+1,y)
第一个公式表示转移t在所有阶段一共出现的次数。第二个公式表示非空转移t,在输出观察的值为y时总共出现的次数。
这样我们就可以用下面的式子估计参数:
q ^ ( y ∣ t ) = c ( y , t ) c ( t ) , t 属于非空转移 \hat{q}{(y|t)}=\frac{c(y, t)}{c(t)}, t属于非空转移 q^(y∣t)=c(t)c(y,t),t属于非空转移
p ^ ( t i ) = { c ( t i ) c ( t 1 ) + c ( t 2 ) + c ( t 3 ) i = 1,2,3 1 i = 4 c ( t i ) c ( t 5 ) + c ( t 6 ) i = 5,6 \hat{p}{(t_i)} = \begin{cases} \frac{c(t_i)}{c(t_1)+c(t_2)+c(t_3)} & \text{i = 1,2,3} \\ 1 & \text{i = 4} \\ \frac{c(t_i)}{c(t_5)+c(t_6)} & \text{i = 5,6} \end{cases} p^(ti)=⎩ ⎨ ⎧c(t1)+c(t2)+c(t3)c(ti)1c(t5)+c(t6)c(ti)i = 1,2,3i = 4i = 5,6
但是我们对于求转移次数的公式 c ( t ) = ∑ i = 0 k − 1 I i ( t ) c(t)=\sum_{i=0}^{k-1}I_i(t) c(t)=∑i=0k−1Ii(t), 和 c ( y , t ) = ∑ i = 0 k − 1 I i ( t ) δ ( y i + 1 , y ) c(y, t)=\sum_{i=0}^{k-1}I_i(t)\delta(y_{i+1}, y) c(y,t)=∑i=0k−1Ii(t)δ(yi+1,y)还有一些问题。那就是我们不知道隐藏状态转移序列 T = t 1 , t 2 , … , t m {T=t_1, t_2, \dots, t_m} T=t1,t2,…,tm,但是我们知道观察输出序列 Y = y 1 , y 2 , … , y k {Y=y_1, y_2, \dots, y_k} Y=y1,y2,…,yk,所以我们可以计算转移t在i阶段发生的可能性 P { t i = t } P\{t^i=t\} P{ti=t},所以公式变成下面这样的新"计数" 公式:
c ( t ) = ∑ i = 0 k − 1 P { t i = t } c(t)=\sum_{i=0}^{k-1}P\{t^i=t\} c(t)=∑i=0k−1P{ti=t}
c ( y , t ) = ∑ i = 0 k − 1 P { t i = t } δ ( y i + 1 , y ) c(y, t)=\sum_{i=0}^{k-1}P\{t^i=t\}\delta(y_{i+1}, y) c(y,t)=∑i=0k−1P{ti=t}δ(yi+1,y)
其中 δ \delta δ的定义为:
δ ( y , y ′ ) = { 1 y = y’,即当前的 y 和要找的 y ′ 是一样的 0 其他情况 \delta(y, y') = \begin{cases} 1 & \text{y = y'},即当前的y和要找的y'是一样的 \\ 0 & \text{其他情况} \end{cases} δ(y,y′)={10y = y’,即当前的y和要找的y′是一样的其他情况
由于阶段从i-1转换到i必然发生一次非空转换,所以对于非空转换t’',就有 ∑ P { t i = t ′ ′ } = 1 {\sum{P}\{t^i =t^{''}\}=1} ∑P{ti=t′′}=1