一、概述

贪心算法是一种常见的算法思想，用于解决优化问题。其基本思想是在每一步选择中都采取当前状态下最优的选择，从而希望能够获得全局最优解。

具体来说，贪心算法通常分为以下步骤：

1. 定义问题的最优解，通常需要将问题转化为求最大值或最小值；
2. 选择一个局部最优解，并将其加入到最终解中；
3. 将局部最优解所对应的子问题规模缩小，并重复步骤2，直到达到最优解。

贪心算法的优点在于其简单、高效，并且可以用于解决许多实际问题，例如：

• 最小生成树问题；
• 最短路径问题；
• 部分背包问题；
• 区间调度问题；
• 分糖果问题等。

然而，贪心算法并不总是能够得到全局最优解，因为其仅考虑当前局部最优解，并没有考虑到未来可能出现的情况。因此，在使用贪心算法时需要仔细思考问题本身的性质，并根据具体问题来选择合适的贪心策略。

二、区间问题

2.1区间选点

给定 N 个闭区间 [ai,bi]，请你在数轴上选择尽量少的点，使得每个区间内至少包含一个选出的点。

输出选择的点的最小数量。

位于区间端点上的点也算作区间内。

输入格式

第一行包含整数 N，表示区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式

输出一个整数，表示所需的点的最小数量。

数据范围

1≤N≤105,
−109≤ai≤bi≤109

输入样例：

3
-1 1
2 4
3 5

输出样例：

2

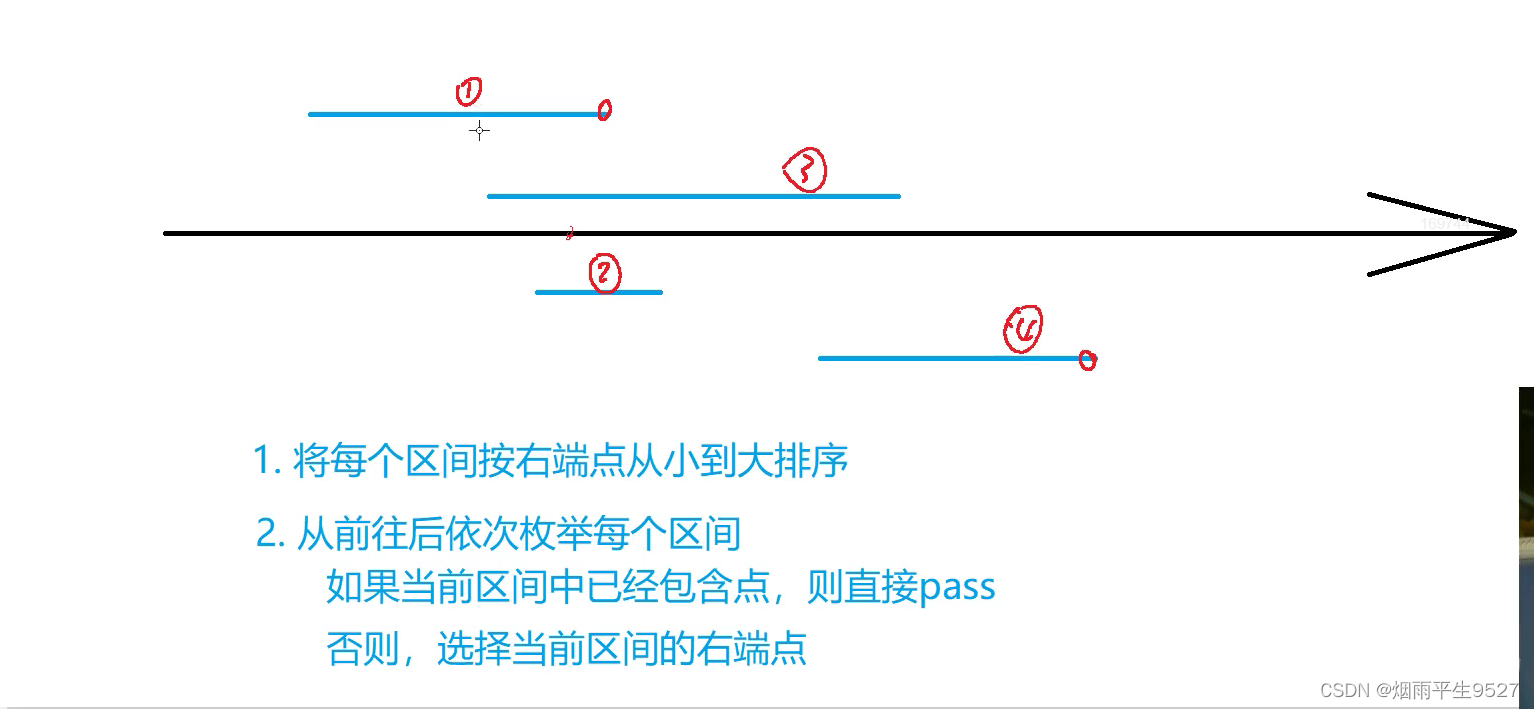
贪心算法

（1）首先将这些区间按照右端点从小到大进行排序，即 bi 升序排序。

（2）初始化一个点 p 为最左端的区间的右端点。

（3）遍历每个区间 [ai, bi]，如果 ai > p，则将 p 更新为 bi，计数器加一。

（4）遍历完所有的区间之后，得到的计数器即为所需的最小点数。

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

struct Range  //定义一个结构体Range，表示一个区间
{
    int l, r;  //区间左右端点
    bool operator < (const Range &W) const  //重载运算符，排序时按照右端点从小到大排序
    {
        return r < W.r;
    }
}range[N];

int n;

int main()
{
    scanf("%d", &n);

    for (int i = 0; i < n; i ++ ) scanf("%d%d", &range[i].l, &range[i].r);

    sort(range, range + n);  //将所有区间按照右端点从小到大排序

    int res = 1, p = range[0].r;  //初始化计数器res为1，p为最左端区间的右端点

    for (int i = 1; i < n; i ++ )  //遍历所有区间
        if (range[i].l > p)  //如果当前区间的左端点比p要大
        {
            res ++ ;  //计数器加一
            p = range[i].r;  //更新p为当前区间的右端点
        }

    printf("%d", res);  //输出所需点的最小数量

    return 0;
}

2.2最大不相交区间数量

给定 N个闭区间 [ai,bi]请你在数轴上选择若干区间，使得选中的区间之间互不相交（包括端点）。

输出可选取区间的最大数量。

输入格式

第一行包含整数 N，表示区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式

输出一个整数，表示可选取区间的最大数量。

数据范围

1≤N≤105
−109≤ai≤bi≤109

输入样例：

3
-1 1
2 4
3 5

输出样例：

2

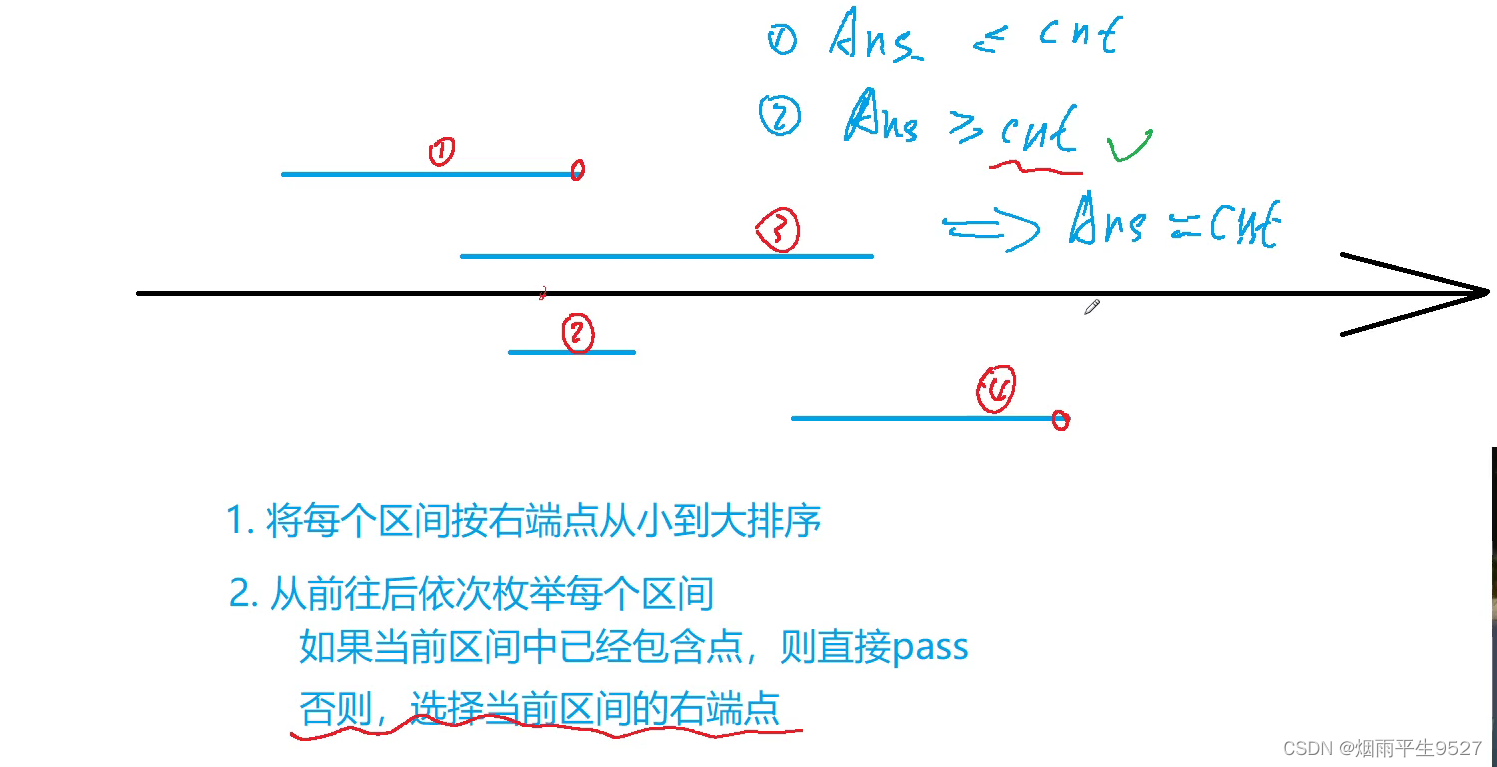
 算法（贪心）

可以参考区间选点那题，二者在算法思路上是一致的

（1）将每个区间按照右端点从小到大进行排序
（2）ed表示当前放置在数轴上的点的位置，开始初始化为无穷小，表示没有放置，此时数轴上没有点
（3）依次遍历排序好的区间。如果区间的左端点大于当前放置点的位置，说明当前点无法覆盖区间，则把点的位置更新成该区间的右端点，表示在该区间的右端点放置一个新的点，同时更新点的个数

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

struct Range  //定义一个结构体Range，表示一个区间
{
    int l, r;  //区间左右端点
    bool operator < (const Range &W) const  //重载运算符，排序时按照右端点从小到大排序
    {
        return r < W.r;
    }
}range[N];

int n;

int main()
{
    scanf("%d", &n);

    for (int i = 0; i < n; i ++ ) scanf("%d%d", &range[i].l, &range[i].r);

    sort(range, range + n);  //将所有区间按照右端点从小到大排序

    int res = 1, p = range[0].r;  //初始化计数器res为1，p为最左端区间的右端点

    for (int i = 1; i < n; i ++ )  //遍历所有区间
        if (range[i].l > p)  //如果当前区间的左端点比p要大
        {
            res ++ ;  //计数器加一
            p = range[i].r;  //更新p为当前区间的右端点
        }

    printf("%d", res);  //输出所需点的最小数量

    return 0;
}

2.3区间分组

给定 N 个闭区间 [ai,bi]，请你将这些区间分成若干组，使得每组内部的区间两两之间（包括端点）没有交集，并使得组数尽可能小。

输出最小组数。

输入格式

第一行包含整数 N，表示区间数。

接下来 N行，每行包含两个整数 ai,bi表示一个区间的两个端点。

输出格式

输出一个整数，表示最小组数。

数据范围

1≤N≤105
−109≤ai≤bi≤109

输入样例：

3
-1 1
2 4
3 5

输出样例：

2

#include <iostream>
#include <algorithm>
#include <queue> // C++ STL 提供的优先队列（堆）实现

using namespace std;

const int N = 100010;

int n;
struct Range
{
    int l, r;
    // 重载小于号，按左端点排序
    bool operator< (const Range &W)const
    {
        return l < W.l;
    }
} range[N];

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i ++ )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        range[i] = {l, r};
    }

    sort(range, range + n); // 按左端点排序

    // 用小根堆维护所有组的右端点的最大值
    // 堆中的每一个值存的是每个组的右端点的最大值
    priority_queue<int, vector<int>, greater<int>> heap; // 创建一个小根堆（优先队列）
    for (int i = 0; i < n; i ++ )
    {
        auto r = range[i];
        // 如果堆为空或者堆的最小右端点 >= 现在区间的左端点，则说明有交集，不能合并，需要新开一个堆
        if (heap.empty() || heap.top() >= r.l) heap.push(r.r);
        // 否则说明至少与最小的右端点的组没有交集，将它放到右端点最小的组里去
        else
        {
            heap.pop(); // 弹出这个区间的最小右端点，插入当前区间的右端点，即将其更新了
            heap.push(r.r);
        }
    }

    // 输出组的数量
    printf("%d\n", heap.size());

    return 0;
}

有若干个活动，第i个活动开始时间和结束时间是【si,sj】同一个教室安排的活动之间不能交叠，求要安排所有活动，少需要几个教室？

有时间冲突的活动不能安排在同一间教室，与该问题的限制条件相同，即最小需要的教室个数即为该题答案。

我们可以把所有开始时间和结束时间排序，遇到开始时间就把需要的教室加1，遇到结束时间就把需要的教室减1,在一系列需要的教室个数变化的过程中，峰值就是多同时进行的活动数，也是我们至少需要的教室数。

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100100;

int n;
int b[2 * N], idx; // 将左右端点拆成两个数，左端点是偶数，右端点是奇数，存储在数组 b 中

int main()
{
    scanf ("%d", &n);
    for(int i = 0; i < n; i ++)
    {
        int l, r;
        scanf("%d %d", &l, &r);
        b[idx ++] = l * 2; // 标记左端点为偶数
        b[idx ++] = r * 2 + 1; // 标记右端点为奇数
    }

    sort(b, b + idx); // 将所有端点按大小排序

    int res = 1, t = 0; // res 存储最终答案，t 维护当前线段数量
    for(int i = 0; i < idx; i ++)
    {
        if(b[i] % 2 == 0) t ++; // 如果是偶数，则是左端点，将 t 加 1
        else t --; // 否则是奇数，是右端点，将 t 减 1
        res = max(res, t); // 更新答案
    }

    printf ("%d\n", res); // 输出答案
    return 0;
}

2.4区间覆盖

给定 N 个闭区间 [ai,bi]以及一个线段区间 [s,t]，请你选择尽量少的区间，将指定线段区间完全覆盖。

输出最少区间数，如果无法完全覆盖则输出 −1−1。

输入格式

第一行包含两个整数 s和 t，表示给定线段区间的两个端点。

第二行包含整数 N，表示给定区间数。

接下来 N 行，每行包含两个整数 ai,bi，表示一个区间的两个端点。

输出格式

输出一个整数，表示所需最少区间数。

如果无解，则输出 −1。

数据范围

1≤N≤105
−109≤ai≤bi≤109
−109≤s≤t≤109

输入样例：

1 5
3
-1 3
2 4
3 5

输出样例：

2

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;
struct Range
{
    int l, r;
    bool operator< (const Range &W)const  // 自定义结构体排序规则
    {
        return l < W.l;
    }
}range[N]; // 定义一个结构体数组range，其中l和r分别表示每个区间的左右端点

int main()
{
    int st, ed; 
    scanf("%d%d", &st, &ed); // 输入起点和终点
    scanf("%d", &n); // 输入区间的个数
    for (int i = 0; i < n; i ++ )
    {
        int l, r;
        scanf("%d%d", &l, &r); // 输入每个区间的左右端点
        range[i] = {l, r}; // 存储区间信息到结构体数组中
    }

    sort(range, range + n); // 对结构体数组进行排序，按照左端点从小到大排序

    int res = 0; // 记录能够覆盖的区间个数
    bool success = false; // 标记是否能够覆盖终点ed
    for (int i = 0; i < n; i ++ )
    {
        int j = i, r = -2e9; // j表示当前区间的右端点能够覆盖的最远位置，r表示当前能够覆盖的最远位置，初始值为负无穷
        while (j < n && range[j].l <= st) // 遍历所有左端点在起点st左边或等于st的区间，更新右端点能够覆盖的最远位置
        {
            r = max(r, range[j].r);
            j ++ ;
        }

        if (r < st) // 如果找不到任何一个区间能够覆盖st，则无法到达终点，返回-1
        {
            res = -1;
            break;
        }

        res ++ ; // 能够找到一个区间覆盖st，将res加1
        if (r >= ed) // 如果该区间能够覆盖ed，则能够到达终点，将success标记为true，结束循环
        {
            success = true;
            break;
        }

        st = r; // 更新起点为当前能够覆盖的最远位置
        i = j - 1;  // 更新i的位置，从当前已经覆盖的区间后面开始查找下一个区间
    }

    if (!success) res = -1; // 如果无法到达终点，则返回-1
    printf("%d\n", res); // 输出能够覆盖的区间个数

    return 0;
}

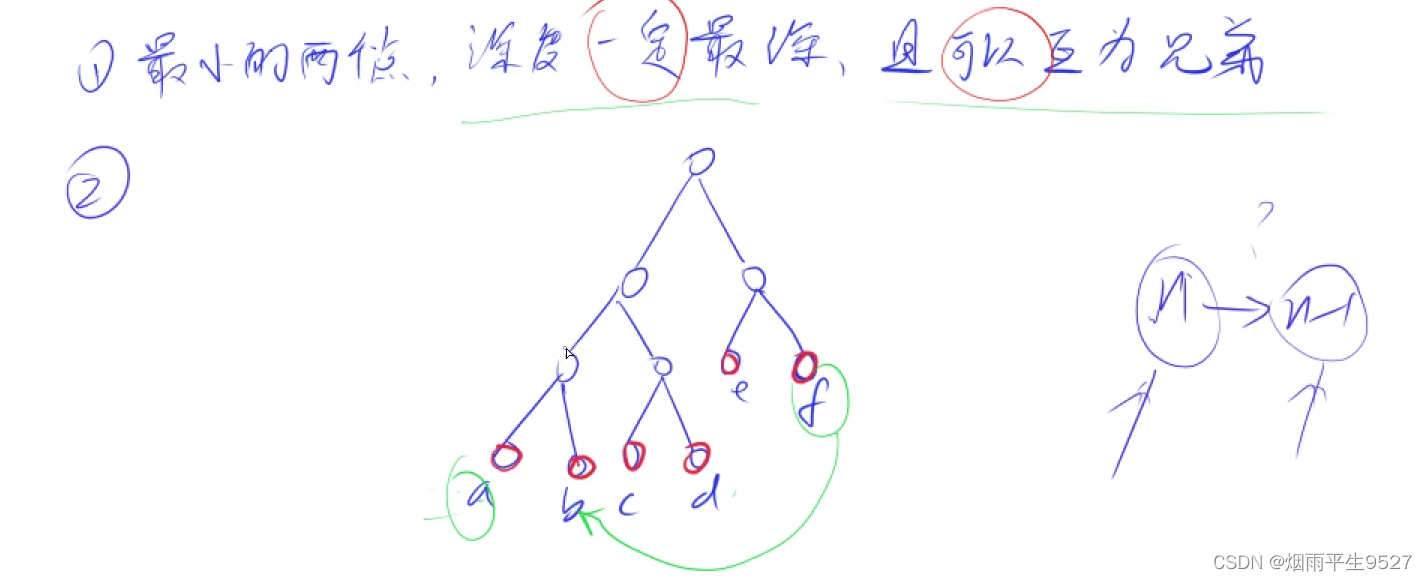
三、Huffman树

3.1合并果子

在一个果园里，达达已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。

达达决定把所有的果子合成一堆。

每一次合并，达达可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。

可以看出，所有的果子经过 n−1 次合并之后，就只剩下一堆了。

达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以达达在合并果子时要尽可能地节省体力。

假定每个果子重量都为 1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使达达耗费的体力最少，并输出这个最小的体力耗费值。

例如有 3种果子，数目依次为 1，2，9。

可以先将 1、2 堆合并，新堆数目为 3，耗费体力为 3。

接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 12，耗费体力为 12。

所以达达总共耗费体力3+12=15。

可以证明 15 为最小的体力耗费值。

输入格式

输入包括两行，第一行是一个整数 n，表示果子的种类数。

第二行包含 n 个整数，用空格分隔，第 i 个整数 ai 是第 i 种果子的数目。

输出格式

输出包括一行，这一行只包含一个整数，也就是最小的体力耗费值。

输入数据保证这个值小于 231231。

数据范围

1≤n≤10000
1≤ai≤20000

输入样例：

3 
1 2 9 

输出样例：

15

#include <iostream>
#include <queue>

using namespace std;

int n;
priority_queue<int, vector<int>, greater<int> > q; //定义一个名为q的小根堆

int main()
{
    scanf("%d", &n);

    while (n --)
    {
        int x;
        scanf("%d", &x);
        q.push(x); //依序插入果子堆
    }

    int res = 0;
    while (q.size() > 1) //当还没有只剩一个果子堆的时候，即还没有合并完的时候
    {
        int a = q.top(); q.pop(); //取第一小值
        int b = q.top(); q.pop(); //取第二小值
        int c = a + b; //消耗体力值 与 新堆果子数

        res += c;
        q.push(c); //插入新果子堆
    }

    printf("%d\n", res);

    return 0;
}

 四、排序不等式

4.1排队打水

有 n 个人排队到 1 个水龙头处打水，第 i 个人装满水桶所需的时间是 ti，请问如何安排他们的打水顺序才能使所有人的等待时间之和最小？

输入格式

第一行包含整数 n。

第二行包含 n 个整数，其中第 i 个整数表示第 i个人装满水桶所花费的时间 ti。

输出格式

输出一个整数，表示最小的等待时间之和。

数据范围

1≤n≤105
1≤ti≤104

输入样例：

7
3 6 1 4 2 5 7

输出样例：

56

#include <iostream>
#include <algorithm> //引入STL的sort函数，方便排序

using namespace std;

const int N = 1e5 + 10; //常量N表示数组t的最大长度

typedef long long LL; //将long long类型定义为LL，方便使用

int t[N]; //定义数组t，用来存放输入的n个数

int main()
{
    int n;
    scanf("%d", &n); //输入n的值
    for (int i = 0; i < n; i ++ )   scanf("%d", &t[i]); //输入n个数，并存放到数组t中

    sort(t, t + n); //对数组t进行排序，从小到大排序

    LL res = 0; //定义res表示结果，并初始化为0
    for (int i = 0; i < n; i ++ )  res += t[i] * (n - i - 1); //计算结果，累加每个数t[i]与其后面所有数的乘积，累加到res中

    printf("%lld\n", res); //输出结果

    return 0;
}

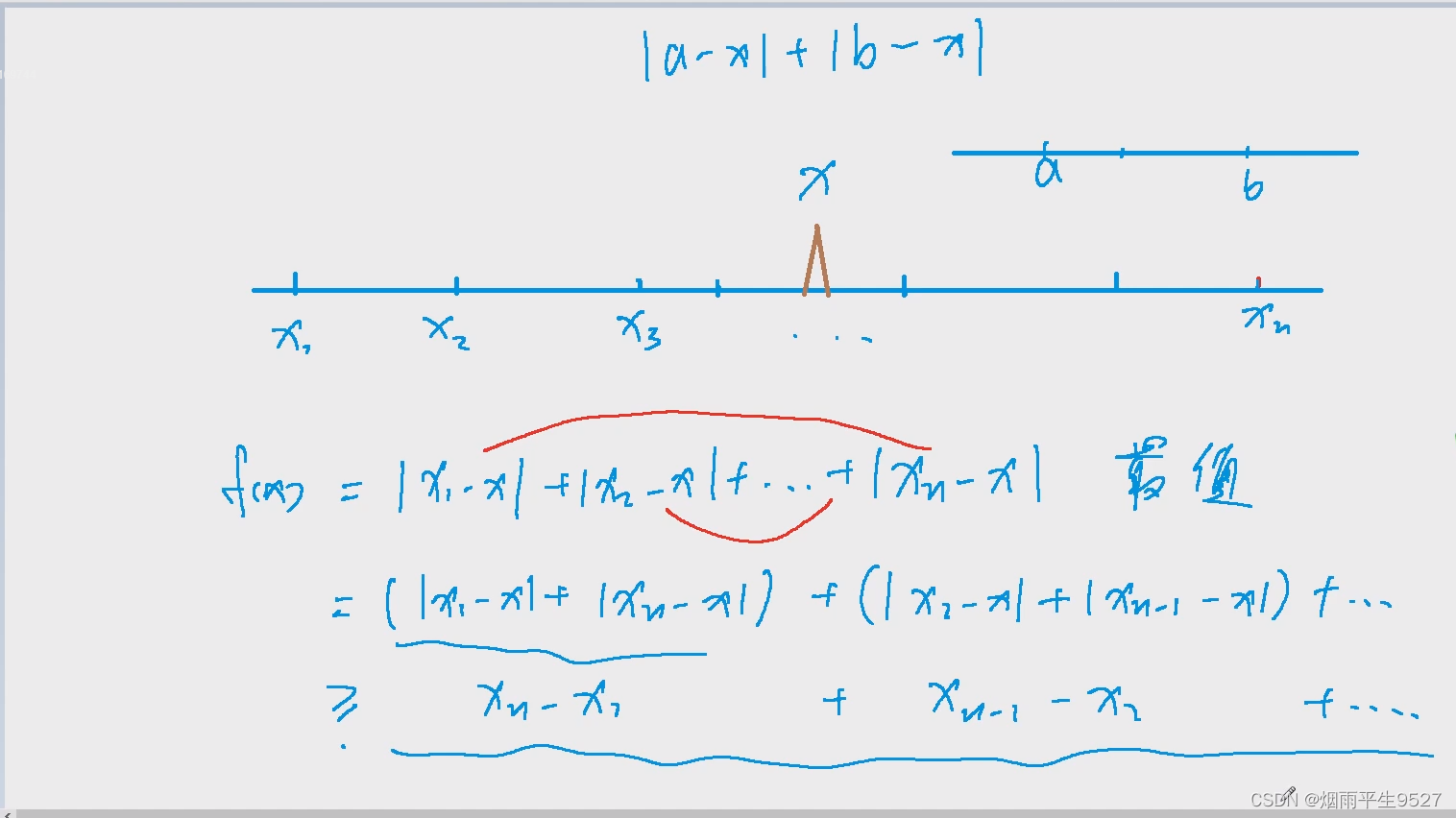
 4.2货仓选址

在一条数轴上有 N家商店，它们的坐标分别为 A1∼AN。

现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。

为了提高效率，求把货仓建在何处，可以使得货仓到每家商店的距离之和最小。

输入格式

第一行输入整数 N。

第二行 N 个整数 A1∼AN

输出格式

输出一个整数，表示距离之和的最小值。

数据范围

1≤N≤100000
0≤Ai≤40000

输入样例：

4
6 2 9 1

输出样例：

12

#include <algorithm> // C++ 标准库中的算法库，包括排序算法

using namespace std;

const int N = 100005; // 声明一个常量

int n, res; // n 表示数组长度，res 表示最终结果
int a[N]; // 声明一个长度为 N 的整型数组 a

int main()
{
    scanf("%d", &n); // 输入数组长度
    for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]); // 输入数组元素

    sort(a, a + n); // 对数组 a 进行升序排序

    // 计算数组 a 中每个元素与中位数之间的距离的绝对值之和
    for (int i = 0; i < n; i ++ ) res += abs(a[i] - a[n >> 1]);

    printf("%d\n", res); // 输出最终结果

    return 0;
}

五、其他常规问题

5.1找零钱

假设你在一家商店购买商品，需要支付一定的现金，并希望得到尽可能少的硬币找零。这个问题可以用贪心算法来解决。下面是一个例子：

假设你需要支付15元，你手上有1元、2元、5元的硬币，如何得到最少数量的硬币找零呢？

#include <iostream>
using namespace std;

int findChange(int amount, int coins[], int n) {
    int count = 0;
    for (int i = n - 1; i >= 0; i--) {
        while (amount >= coins[i]) {
            amount -= coins[i];
            count++;
        }
    }
    return count;
}

int main() {
    int coins[] = {5, 2, 1};  // 硬币面额
    int n = sizeof(coins) / sizeof(coins[0]);  // 硬币种类数
    int amount = 15;  // 需要找零的金额
    int numCoins = findChange(amount, coins, n);  // 找零所需最小硬币数
    cout << "最少需要" << numCoins << "个硬币来找零" << endl;
    return 0;
}

5.2活动安排问题

活动安排问题(贪心)

有若干个活动，第i个开始时间和结束时间是[Si,fi)，同一个教室安排的活动之间不能交叠，求要安排所有活动，最少需要几个教室？

Input 第一行一个正整数n (n <= 10000)代表活动的个数。 第二行到第(n + 1)行包含n个开始时间和结束时间。 开始时间严格小于结束时间，并且时间都是非负整数，小于1000000000

Output 一行包含一个整数表示最少教室的个数。

Sample Input 3 1 2 3 4 2 9

Sample Output 2

// 活动安排问题(贪心)
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100100;

int n;
int b[2 * N], idx; // 将左右端点拆成两个数，左端点是偶数，右端点是奇数，存储在数组 b 中

int main()
{
    scanf ("%d", &n); // 输入活动的个数
    for(int i = 0; i < n; i ++)
    {
        int l, r;
        scanf("%d %d", &l, &r); // 输入每个活动的开始时间和结束时间
        b[idx ++] = l * 2; // 将左端点乘以2作为偶数存储在数组b中
        b[idx ++] = r * 2 + 1; // 将右端点乘以2加1作为奇数存储在数组b中
    }

    sort(b, b + idx); // 将所有端点按大小排序

    int res = 1, t = 0; // res 存储最终答案，t 维护当前线段数量
    for(int i = 0; i < idx; i ++)
    {
        if(b[i] % 2 == 0) t ++; // 如果是偶数，则是左端点，将 t 加 1
        else t --; // 否则是奇数，是右端点，将 t 减 1
        res = max(res, t); // 更新答案，取当前的最大值
    }

    printf ("%d\n", res); // 输出答案，即教室数量
    return 0;
}

5.3 最优装载问题

任务描述 有一天，海盗截获了一艘装满各种各样古董的货船，每一件古董都价值连城，一但打碎就失去了价值，虽然海盗船足够大，但载重量为C，每件古董的重量为Wi，海盗们如何把尽量多的宝贝装上海盗船呢？

输入格式 第一行输入n，c，代表有n个古董和船的重量 第二行输入n个数，代表每个古董的重量。 1<n,c<100000 每个古董的重量不超过100

输出格式 输出一个数，代表最多装多少个古董

输入样例 8 30 4 10 7 11 3 5 14 2

输出样例 5

#include <iostream>
#include <algorithm>
using namespace std;

const int MAXN = 10005;
int w[MAXN];

bool cmp(int a, int b) {
    return a > b;
}

int main() {
    int n, c;
    cin >> n >> c;
    for (int i = 1; i <= n; i++) {
        cin >> w[i];
    }
    sort(w + 1, w + n + 1, cmp);
    int sum = 0, cnt = 0;
    for (int i = 1; i <= n; i++) {
        if (sum + w[i] <= c) {
            sum += w[i];
            cnt++;
        } else {
            break;
        }
    }
    cout << cnt << endl;
    return 0;
}

5.4最优分解问题

设n是一个正整数。现在要求将n分解为若干个互不相同的自然数的和，且使这些自然数的乘积最大。 编程任务： 　　对于给定的正整数n，编程计算最优分解方案。 数据输入： 　　第1 行是正整数n。 结果输出: 　　计算出的最大乘积。 输入示例 　　10 输出示例 　　30=2*3*5 输入20，则输出2*3*4*5*6=720

#include <iostream>
using namespace std;

void taixin(int n){
    int a[100]; // 临时数组，保存分解后的数
    int k = 1; // a数组的索引
    int sum = 1; // 最大乘积
    int i; // 索引
    if (n < 5){ // 如果小于5，那么都是乘积是1*n ；
        sum = n;
    } else {
        a[1] = 2;
        n -= 2;
        while (n > a[k]) {
            k++;
            a[k] = a[k - 1] + 1;
            n = n - a[k];
        }
        if (n == a[k]) {
            a[k]++;
            n--;
        }
        for (i = 0; i < n; i++) {
            a[k - i]++;
        }
        for (i = 1; i <= k; i++) {
            sum *= a[i];
        }
        cout << "分解后的数: ";
        for (i = 1; i <= k; i++) {
            cout << a[i] << " ";
        }
    }
    cout << "\n最大的成绩: " << sum << endl;
}

int main() {
    int n;
    cout << "请输入正整数n：";
    cin >> n;
    taixin(n);
    return 0;
}