时间复杂度

何为时间复杂度

算法的时间复杂度，是一个用于度量一个算法的运算时间的一个描述，本质是一个函数，根据这个函数能在不用具体的测试数据来测试的情况下，粗略地估计算法的执行效率，换句话讲时间复杂度表示的只是代码执行时间随数据规模增长的变化趋势。在数据结构中，算法的时间复杂度常用大O来表述。

大O表示法

大O表示法是一种特殊的表示法，指出了算法的速度是属于哪一个数量级的。

大O表示法的数学语言描述如下：

算法的时间复杂度通常用大O符号表述，定义为T[n] = O(f(n))。称函数T(n)以f(n)为界或者称T(n)受限于f(n)。如果一个问题的规模是n，解这一问题的某一算法所需要的时间为T(n)。T(n)称为这一算法的“时间复杂度”。当输入量n逐渐加大时，时间复杂度的极限情形称为算法的“渐近时间复杂度”。

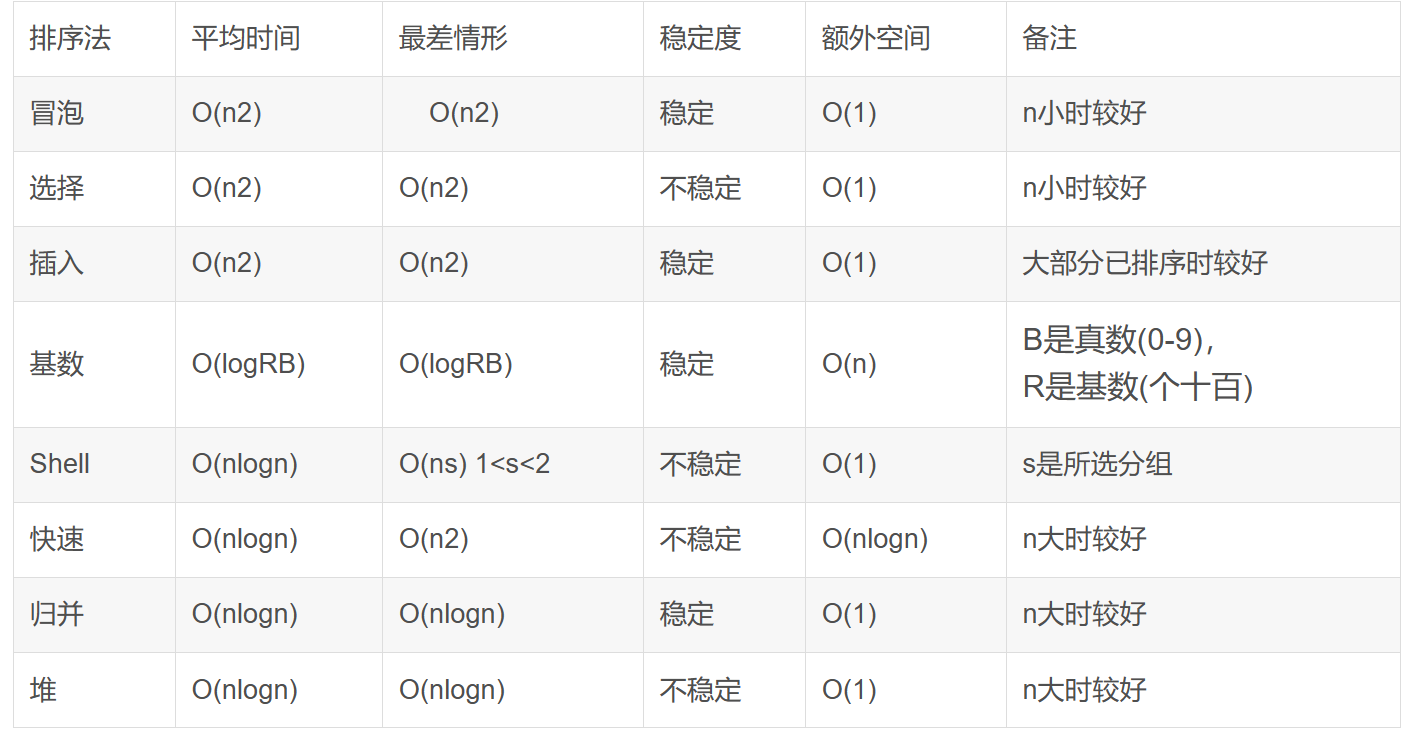
简单来说就是一个程序执行次数的估计值是在哪一个数量级的，例如八种常见排序算法的时间复杂度复杂度如下：

分析算法时间复杂度的基本方法

首先找出计算语句执行次数的数量级，接着用大O表示法来表示

例如下面这个for循环的语句要执行n次（主要是里面的i<=n要执行n次），所以它的时间复杂度是O(n）

for (i=1; i<=n; i++) 
　　    x++;

而下面这段代码的，第一个for循环的语句要执行n次（主要是里面的i<=n要执行n次），第二个for循环的语句要执行n次（主要是里面的j<=n要执行n次），所以它的时间复杂度是O(n^2）

for (i=1; i<=n; i++)
　　    for (j=1; j<=n; j++)
　　        x++;

特殊规则
1) 加法规则
T(n,m) = T1(n) + T2(n) = O (max ( f(n), g(m) )

2) 乘法规则
T(n,m) = T1(n) * T2(m) = O (f(n) * g(m))

3) 常量规则
在大O表示法里面有一个特例，如果T1(n) ＝ O(c)， c是一个与n无关的任意常数，T2(n) = O ( f(n) ) 则有
T(n) = T1(n) * T2(n) = O ( c*f(n) ) = O( f(n) )

也就是说，在大O表示法中，任何非0正常数都属于同一数量级，记为O(1)。

时间复杂度分析示例

for(i=1;i<=n;i+ +)
   for(j=1j<=n;j++) {
       c[i][j]=0;
       for{k= =1:k<=n;k++)
          c[i]I[j]=c[i][j]+ a[i][k]*b[k][j]; 
}

时间复杂度：n*n*n=n3;

i=1;
while（i<=n)
    i=i*2;

分析：

关键是要找出来执行次数x与n的关系，并表示成n的函数
若循环执行1次: i=1*2=2，
若循环执行2次: i=2*2=22（2的平方哈，下面依次）
若循环执行3次: i=2*2=23
.......
若循环执行x次: i=2x（2的x平方哈，下面依次）
又因为i要小于等于n
则2x<=n . 求出x<=log2n

所以时间复杂度为O(logN)

空间复杂度

何为空间复杂度

空间复杂度也是一个数学表达式，它是用来对算法在运行过程中临时占用存储空间大小的度量。

这里也有一个常见误区，空间复杂度并不是计算程序占用了多少字节的空间，这样做是意义不大的。所以空间复杂度计算的是变量的个数。同时间复杂度一样，空间复杂度也是采用的大O渐进表示法。

由于函数运行时所需要的栈空间（如存储参数、局部变量等）在预处理期间就已经确定好了，因此空间复杂度大多数是通过函数在运行时申请的额外空间来确定的。

空间复杂度分析示例

由于我们已经了解了时间复杂度，所以很多内容就不需要再赘述了，这里我们直接通过示例分析来理解空间复杂度的计算。

示例1

void BubbleSort(int* a, int n)
{
     assert(a);
     for (size_t end = n; end > 0; --end)
     {
         int exchange = 0;
         for (size_t i = 1; i < end; ++i)
         {
             if (a[i-1] > a[i])
         {
             Swap(&a[i-1], &a[i]);
             exchange = 1;
         }
     }
         if (exchange == 0)
             break;
     }
}

乍一看，有两个for循环，像是O(N^2)的空间复杂度，但其实不是，这里并没有使用的空间，只有线性（即常数级）的变量。所以这里的空间复杂度是O(N^2)。

也许看第一个示例还是云里雾里的，但不要在此纠结，继续看下面两个示例，会慢慢拨云见日的。

示例2

long long* Fibonacci(size_t n)
{
     if(n==0)
     return NULL;
 
     long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
     fibArray[0] = 0;
     fibArray[1] = 1;
     for (int i = 2; i <= n ; ++i)
     {
         fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
     }
     return fibArray;
}

算法中额外开辟了N个空间（指的是malloc申请的空间），所以空间复杂度为O(N)

示例3

long long Fac(size_t N)
{
     if(N == 0)
     return 1;
 
     return Fac(N-1)*N;
}

算法中递归调用了N次，开辟了N个栈帧，每个栈帧中没有额外开辟空间，即空间复杂度为O(N)。

结果分析：

要注意，这里的空间复杂度与时间复杂度的理解上有些出入。虽然主观感觉这个函数是递归调用了O(2^N)次，应该是开辟2^N块空间，但实际上并不是，因为函数在调用时并不是一直在占用，所以当一个函数执行完毕后，栈帧销毁，这块空间就释放了，下一次递归时就相当于并没有使用更多的空间。所以相当于这里的空间复杂度就是，走到最深层递归调用所占用的空间。

所以相当于空间复杂度的求法是考虑所能使用的最大空间。而时间复杂度是，只要执行一次就将这次执行的时间算进去。所以可以这样来理解 “时间是一去不复返的，用了多少就算多少；空间是可以循环利用的；能用多少就算多少”。

常见的复杂度等级比较

下表是按照时间（空间）复杂度的执行时间（执行空间）从上到下依次递增。数据结构中log如果没有特殊说明一般都是默认以2为底的。

执行次数	名称级别	大O记法
c（c是常量）	常数级	O(1)
logN	对数级	O(logN)
√N	根号级	O(√N)
log²N	对数平方级	O(log²N)
N	线性级	O(N)
NlogN	线性对数级	O(NlogN)
Nlog²N	线性对数平方级	O(N(log²N))
N²	平方级	O(N²)
N³	立方级	O(N³)
2ⁿ	指数级	O(2ⁿ)