1005. K 次取反后最大化的数组和

思路：给数组按照绝对值大小排序，优先将负数转成正数。如果此时 k % 2 == 1 。最后再将绝对值最小的值变成负数（该值可能原本是负数）
而不是直接从小到大排序。
例如-8，-5，-5，-3，-2，9这种序列。如果直接从小到大排序，那么最后一个变符号的就会是9，但其实让2变成-1更好。

class Solution {
public:
    static bool cmp(int a,int b){
        return abs(a) > abs(b);
    }
    int largestSumAfterKNegations(vector<int>& nums, int k) {
        sort(nums.begin(),nums.end(),cmp);
        for(int i = 0; i < nums.size(); ++i){
            if(nums[i] < 0 && k >0){
                nums[i] *= -1;
                k--;
            }
        }
        if(k%2 == 1) nums[nums.size()-1] *= -1;
        int sum = 0;
        for(int a : nums) sum += a;
        return sum;
    }
};

134. 加油站

如果总油量减去总消耗大于等于零那么一定可以跑完一圈，说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。

每个加油站的剩余量rest[i]为gas[i] - cost[i]。

i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，因为这个区间选择任何一个位置作为起点，到i这里都会断油，那么起始位置从i+1算起，再从0计算curSum。
跟53. 最大子数组和很像

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        deque<int> que;
        int sum = 0;
        for(int i = 0; i < gas.size(); i++){
            que.push_back(gas[i] - cost[i]);
            sum += gas[i] - cost[i];
        }
        if(sum < 0) return -1;
        sum = 0;
        int index = 0;
        for(int i = 0; i < gas.size(); i++){
            sum += que[i];
            if(sum < 0){
                sum = 0;
                index = i+1;
                continue;
            }
        }
        return index;
    }
};

135. 分发糖果

初始思路：
将元素放入map（从小到大排序）然后遍历分数数组去找对应的值，找到以后就判断左右，如果比中间值大，大的那个加一。但是这样的话时间复杂度就会到O(n²)。
卡哥思路：
先确定右边评分大于左边的情况（也就是从前向后遍历）
此时局部最优：只要右边评分比左边大，右边的孩子就多一个糖果，全局最优：相邻的孩子中，评分高的右孩子获得比左边孩子更多的糖果
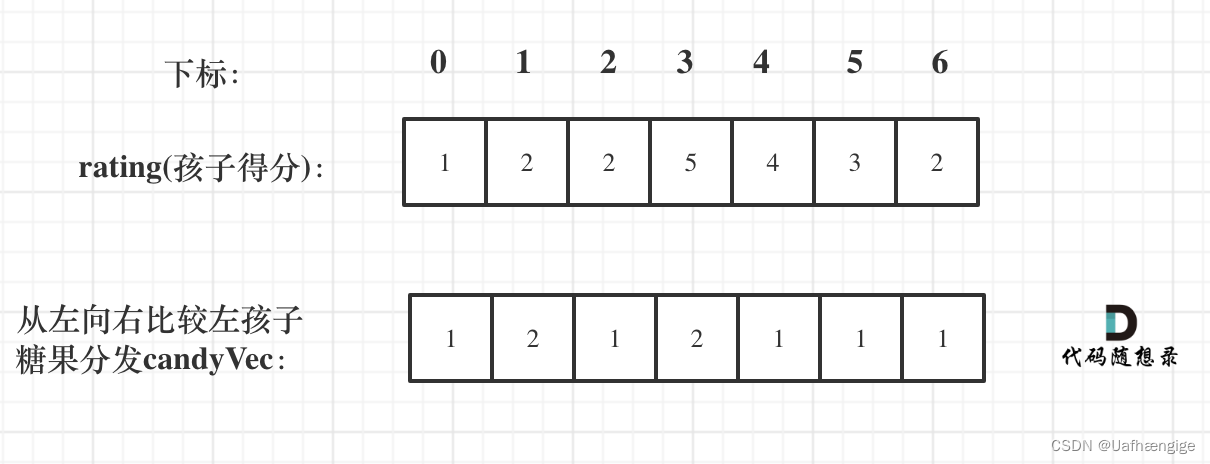从前向后遍历，且被比较的是rating[i]，i从1开始
每次比较都是：if(rating[i] > rating[i-1])。比如比较index0和index1的元素，可能改动的是index1。0是已经定好，不会再改动的。

但是！如果是比较右边元素！就不能从前向后遍历！
例如 5 4 3这组数据
比较index0和index1，此时会根据index1改变index0（本来分数5分数4的孩子都有一颗糖果，5>4，所以分数5再给一颗变成2）。但是比较index2和index1的时候，此时会根据index2改变index1（分数4的孩子有2两颗了）。index1被改变！
index1改变以后，index0就不一定有效了！（此时分数5和分数4都是两颗，没有做到分数5的比分数4的多一颗）
。

class Solution {
public:
    int candy(vector<int>& ratings) {
        vector<int> candy(ratings.size(),1);
        for(int i = 1; i< ratings.size();++i){
            if(ratings[i] > ratings[i-1]) candy[i] = candy[i-1] + 1;
        }
        for(int j = ratings.size()-2; j>=0; --j){
            if(ratings[j] > ratings[j+1]){
                candy[j] = max(candy[j],candy[j+1]+1);
            }
        }
        int sum = 0;
        for(int a : candy) sum += a;
        return sum;
    }
};