一 问题描述

X 村的人们住在美丽的小屋里。若两个小屋通过双向道路连接，则可以说这两个小屋直接相连。X 村非常特别，可以从任意小屋到达任意其他小屋，每两个小屋之间的路线都是唯一的。温迪的孩子喜欢去找其他孩子玩，然后打电话给温迪：“妈咪，带我回家！”。在不同的时间沿道路行走所需的时间可能不同。温迪想告诉她的孩子她将在路上花的确切时间。

二 输入和输出说明

1 输入

第 1 行包含 3 个整数 n 、q 、s，表示有 n 个小屋、q 个消息，温迪目前在 s 小屋里，n <100001，q <100001。以下 n -1 行各包含 3 个整数 a、b 和 w ，表示有一条连接小屋 a 和 b 的道路，所需的时间是 w （1≤w≤10000）。以下 q 行有两种消息类型：

① 消息 A，即 0 u ，孩子在小屋 u 中给温迪打电话，温迪应该从现在的位置去小屋 u ；

② 消息 B，即 1 i w ，将第 i 条道路所需的时间修改为 w 

注意：温迪在途中时，时间不会发生改变，时间在温迪停留在某个地方等待孩子时才会改变）。

2 输出

对每条消息 A，都输出一个整数，即找到孩子所需的时间。

三 输入和输出用例

1 输入样例

3 3 1

1 2 1

2 3 2

0 2

1 2 3

0 3

2 输出样例

1

3

四 分析

本问题中任意两个小屋都可以相互到达，且路径唯一，明显是树形结构。可以将边权看作点权，对一条边，让深度 dep 较大的点存储边权。对边 u 、v ，边权为 w ，若 dep[u ]>dep[v ]，则视 u 的权值为 w 。本问题包括树上点更新、区间和查询。可以用树链剖分将树形结构线性化，然后用线段树进行点更新、区间和查询。

解决方案：树链剖分+线段树。

五 算法设计

1 第 1 次深度优先遍历求 dep、fa、size、son，第 2 次深度优先遍历求 top、id、rev。

2 创建线段树。

3 点更新，u 对应的下标 i =id[u]，将其值更新为 val。

4 区间查询，求 u 、v 之间的和值。若 u 、v 不在同一条重链上，则一边查询，一边向同一条重链靠拢；若 u 、v 在同一条重链上，则根据节点的下标在线段树中进行区间查询。

注意：因为在本题中是将边权转变为点权，所以实际查询的区间应为 query(1, id[son[u]], id[v])。

六 代码

package com.platform.modules.alg.alglib.poj2763;

public class Poj2763 {
    private int maxn = 100010;
    int head[] = new int[maxn]; //头结点
    int cnt = 0;
    int total = 0;
    int fa[] = new int[maxn]; // 父亲
    int dep[] = new int[maxn]; // 深度
    int size[] = new int[maxn]; // 子树结点总数
    int son[] = new int[maxn]; // 重儿子
    int top[] = new int[maxn]; // 所在重链顶端结点
    int id[] = new int[maxn];
    int rev[] = new int[maxn]; // u 对应的 dfs 序下标，下标对于的 u
    int Sum;
    Edge1 a[] = new Edge1[maxn];

    edge e[] = new edge[maxn << 1];

    node tree[] = new node[maxn << 2];

    public Poj2763() {
        for (int i = 0; i < a.length; i++) {
            a[i] = new Edge1();
        }
        for (int i = 0; i < e.length; i++) {
            e[i] = new edge();
        }
        for (int i = 0; i < tree.length; i++) {
            tree[i] = new node();
        }
    }

    public String output = "";

    public String cal(String input) {
        int n, q, s;
        init();

        String[] line = input.split("\n");
        String[] words = line[0].split(" ");
        n = Integer.parseInt(words[0]);
        q = Integer.parseInt(words[1]);
        s = Integer.parseInt(words[2]);

        for (int i = 1; i < n; i++) {
            String[] info = line[i].split(" ");
            a[i].u = Integer.parseInt(info[0]);
            a[i].v = Integer.parseInt(info[1]);
            a[i].w = Integer.parseInt(info[2]);
            add(a[i].u, a[i].v);
            add(a[i].v, a[i].u);
        }
        dep[1] = 1;
        dfs1(1, 0);
        dfs2(1, 1);
        build(1, 1, total);//创建线段树
        for (int i = 1; i < n; i++) {
            if (dep[a[i].u] > dep[a[i].v]) {
                int temp = a[i].u;
                a[i].u = a[i].v;
                a[i].v = temp;
            }
            update(1, id[a[i].v], a[i].w);
        }
        int opt, i, val, x;
        while (q-- > 0) {
            String[] query = line[n++].split(" ");
            opt = Integer.parseInt(query[0]);

            if (opt == 1) {
                i = Integer.parseInt(query[1]);
                val = Integer.parseInt(query[2]);
                update(1, id[a[i].v], val); // 改变第 i 条边的值为 val
            } else {
                x = Integer.parseInt(query[1]);
                Sum = 0;
                ask(s, x);//查询s->x路径上边权的和值
                output += Sum + "\n";
                s = x;//更新温迪的位置
            }
        }
        return output;
    }

    void add(int u, int v) {
        e[++cnt].to = v;
        e[cnt].next = head[u];
        head[u] = cnt;
    }

    void init() {
        cnt = total = 0;
    }

    // 求dep,fa,size,son
    void dfs1(int u, int f) {
        size[u] = 1;
        for (int i = head[u]; i > 0; i = e[i].next) {
            int v = e[i].to;
            if (v == f)//父节点
                continue;
            dep[v] = dep[u] + 1;//深度
            fa[v] = u;
            dfs1(v, u);
            size[u] += size[v];
            if (size[v] > size[son[u]])
                son[u] = v;
        }
    }

    // 求 top,id,rev
    void dfs2(int u, int t) {
        top[u] = t;
        id[u] = ++total;//u对应的dfs序下标
        rev[total] = u;//dfs序下标对应的结点u
        if (son[u] == 0)
            return;
        dfs2(son[u], t);//沿着重儿子dfs
        for (int i = head[u]; i > 0; i = e[i].next) {
            int v = e[i].to;
            if (v != fa[u] && v != son[u])
                dfs2(v, v);
        }
    }

    // 点更新，线段树的第 k 个值为 val
    void update(int i, int k, int val) {
        if (tree[i].l == k && tree[i].r == k) {
            tree[i].sum = val;
            return;
        }
        int mid = (tree[i].l + tree[i].r) / 2;
        if (k <= mid) update(i << 1, k, val);
        else update((i << 1) | 1, k, val);
        tree[i].sum = tree[i << 1].sum + tree[(i << 1) | 1].sum;
    }

    // 初始化线段树,i 表示存储下标,区间[l,r]
    void build(int i, int l, int r) {
        tree[i].l = l;
        tree[i].r = r;
        tree[i].sum = 0;
        if (l == r) return;
        int mid = (l + r) / 2;//划分点
        build(i << 1, l, mid);
        build((i << 1) | 1, mid + 1, r);
    }

    // 查询线段树中 [l,r] 的和值
    void query(int i, int l, int r) {
        if (tree[i].l >= l && tree[i].r <= r) {//找到该区间
            Sum += tree[i].sum;
            return;
        }
        int mid = (tree[i].l + tree[i].r) / 2;
        if (l <= mid) query(i << 1, l, r);
        if (r > mid) query((i << 1) | 1, l, r);
    }

    void ask(int u, int v) {//求u,v之间的和值
        while (top[u] != top[v]) {//不在同一条重链上
            if (dep[top[u]] < dep[top[v]]) {
                int temp = u;
                u = v;
                v = temp;
            }

            query(1, id[top[u]], id[u]);//u顶端结点和u之间
            u = fa[top[u]];
        }
        if (u == v) return;
        if (dep[u] > dep[v]) {//在同一条重链上
            int temp = u; //深度小的结点为u
            u = v;
            v = temp;
        }
        query(1, id[son[u]], id[v]);//注意是son[u]
    }
}

class edge {
    int to, next;
}

// 结点
class node {
    int l, r, sum; // l,r区间左右端点，区间和值
}

class Edge1 {
    int u, v, w;
}

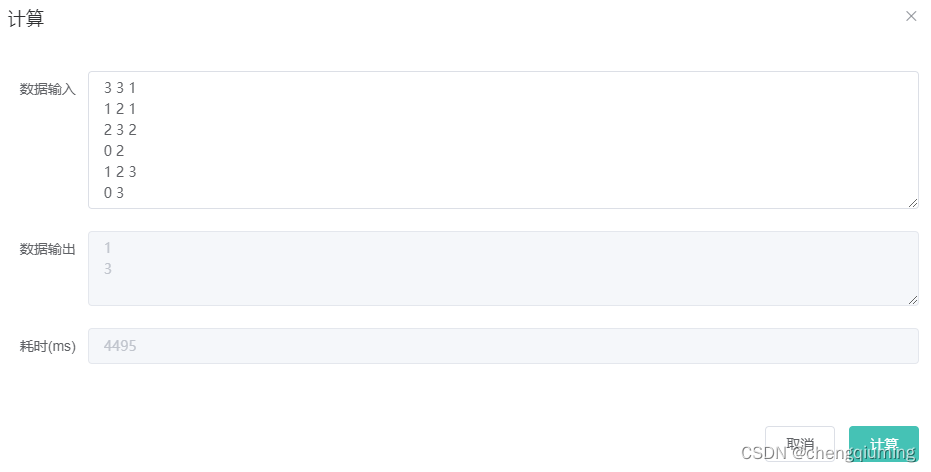
七 测试