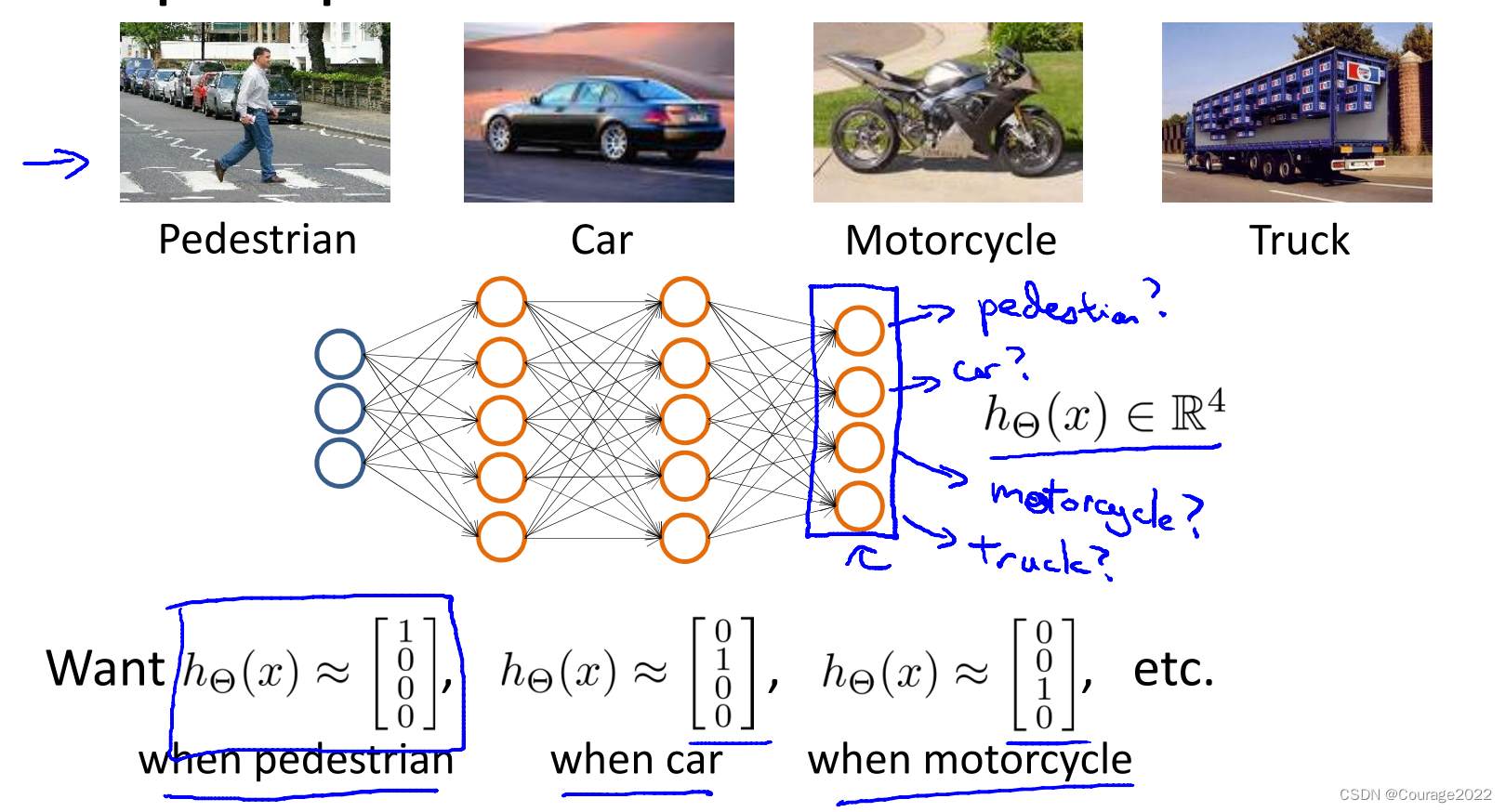
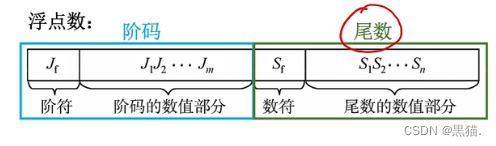
浮点数表示
浮点数的表示分为阶码和尾数;
比如3.026*1011;阶码是+11;尾数是3.026;
对于阶码:
阶符为正,小数点向后移n位(n表示阶的大小);
阶符为负,小数点向前移n位(n表示阶的大小);
对于尾数:
数符表示正负,数值表示绝对值的大小;
显然尾数的位数越多,表示的数字的精度越高:
3.026104=30260;
3.0265104=30265;
阶码和尾数的表示:
二进制浮点数如何确定真值?

阶码用E表示,尾数用M表示,r=2(阶码的底数,通常为你是二进制就是2,是十进制就是10,但是也可以是4,8等等);
所以浮点数的真值表示可以有上图公式计算得出;

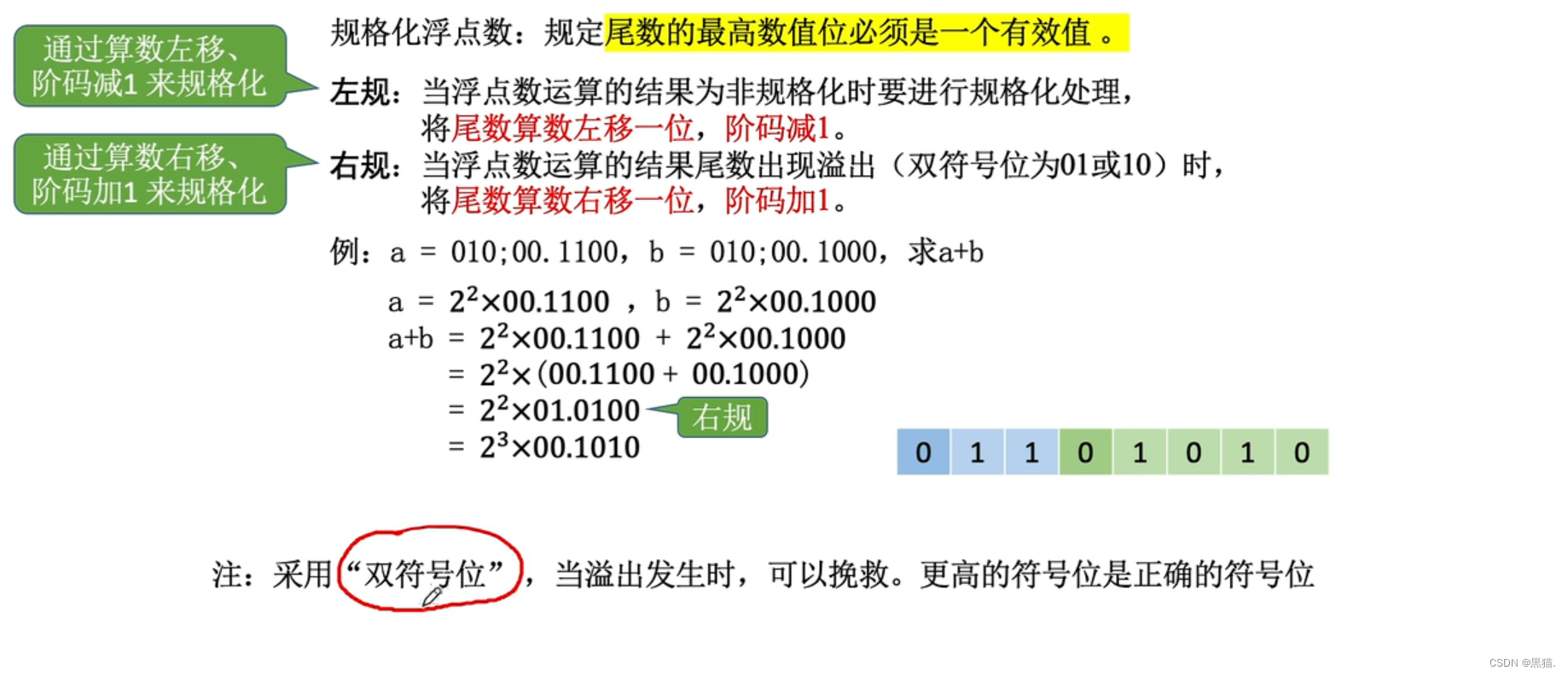
浮点数的规格化


因此对于b: 010;0.01001;如果采用1B的空间来存储浮点数b的话,那么因为是9位:010001001,所以最后一位1会被舍弃,从而丢失了一些精度;但是数值位的最高位(符号位必须保留)却是0,是无效的数值位;因此对于b可以进行规格化:将尾数的数值位全部左移一位,0.01001变成了0.1001,同时阶码-1:010->001;于是就保留了精度;010 0 01001 -》001 0 1001(8位)
双符号位与溢出的挽救
尾数的表示范围
1.用原码表示的位数的表示范围(数值位的最高位必须是1,如果最高位不是1需要进行规格化,因为最高位是0的话是无效位)

类比定点小数的表示范围:

重述一下顶点小数的补码的表示范围为什么是-1~ 1-2-(n-1):
对于定点整数
设位数一共为8位
原码表示范围为 -127-127,即1111 1111~0111 1111
反码表示范围为 -127-127,即1000 0000~0111 1111
补码表示范围为 -128-127,即1000 0000~0111 1111
我们可以尝试求一下-128的原码,但可以发现7位二进制表示不出来,必须得用8位二进制表示,但这样符号位就被占用了。但由于上面说的补码比原码和补码少一个0的表示方法,这就让补码多了一个10000000来表示其他的数,这里具体的细节我也不是很懂@_@,但可以这样记吧,-1到-127已经有对应的原码和补码了,所以也会有对应的补码,而10000000首位是1代表负数,不能和其他数的表示起冲突所以就是-128了。由此,补码可以表示128个负数,1个0以及127个负数共256个数
对于定点小数
还是设位数一共8位
原码表示范围为1.111 1111 ~0.111 1111,即-127/128到127/128
反码表示范围为1.000 0000~0.111 1111,即-127/128到127/128
补码表示范围为1.000 0000~0.111 1111,即-1到127/128
在这里原码和反码都好理解,就是补码会有一个问题,为什么补码会有一个1.000 0000而且居然对应的值是-1,也就是说如果小数用补码表示的话最小值是-1。这里如果用一开始说的取反加一你会发现根本不是这个值。之后才知道取反加一靠的是原码,但看前面原码的定义公式你会发现原码根本表示不了定点小数-1,原码所能表示的是定点整数-1,定点小数-1这里严谨一点的话其实是-1.0。
这里要求定点小数-1.0的补码的话就要用到上面的补码定义公式了(要不然我怎么会贴hhh),由公式可知,-1.0的补码为2+X = 2-1.0 = 1.000 0000
当然也有这样的理解
总结:由于补码表示0的唯一性,补码比原码少一个-0的表示,多一个-1的表示以及负整数表示范围多了一个-128
PS:主要是把自己最近碰到的问题写一下让自己记牢一些。其实如果把上面贴的几个公式吃透的话这些问题根本不会有的orz,注意对比原码反码补码边界的取值你会发现其实说的就是这些东西orz
有关定点整数和小数的表示范围详细还请参考传送门
对于用补码表示的尾数的取值范围,当符号位是1的时候数值为最高位必须是0,符号位为0的时候,数值位的最高位是1,这样有利于硬件的设计;

补码表示的浮点数的规格化

1.1110100 -> 1.0100000然后110要-3->011;
结果0011;1.0100000;


![[附源码]计算机毕业设计JAVA 宠物医院管理系统](https://img-blog.csdnimg.cn/94d247256cf14ca49790bc3a9f8c39dc.png)