文章目录

二叉搜索树
平衡搜索树
- AVL树
- - 定义
  - - AVL中平衡(Balance)因子的定义
  - AVL树插入规则
  - - AVL树失衡情况
    - - 左左失衡/右右失衡
      - 左右失衡
      - RL失衡
  - 代码
  - - 左旋-调整平衡
    - 插入
    - 调整平衡因子
    - AVL树正确性的验证

二叉搜索树

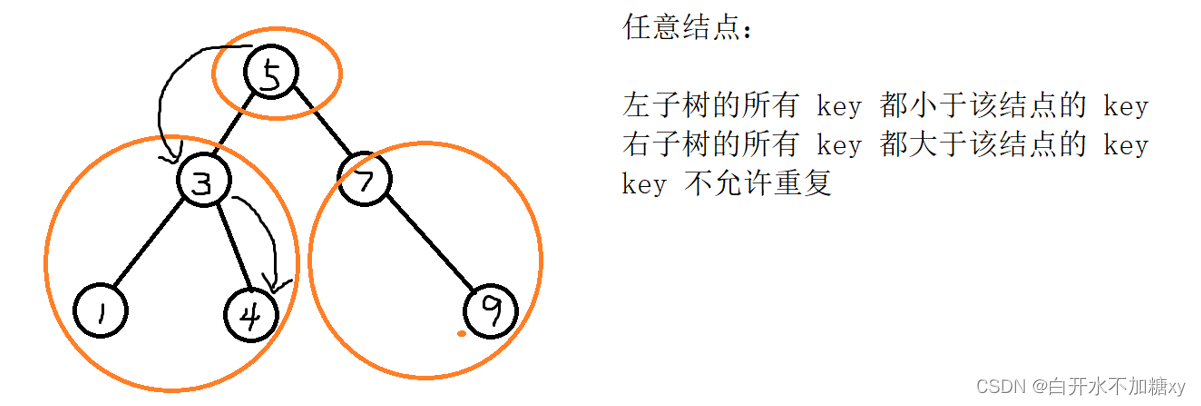
在这里插入图片描述
理想情况下，二叉搜索树的查找时间复杂度是0(log(n))
但是，在退化的情况下，变成0(n)，进而导致插入/删除的时间复杂度也退化为0(n)

为了解决上述问题，引入了平衡树的概念

严格:高度不会“相差”
宽泛:高度不会“相差”太多

由此，使得查找、插入删除等复杂度不会太高。

平衡搜索树

AVL树

定义

二叉平衡搜索树

AVL树在二叉搜索树的基础上要求:任意结点，左右子树的高度差的绝对值不能超过1
高度差= [-1，0，1]

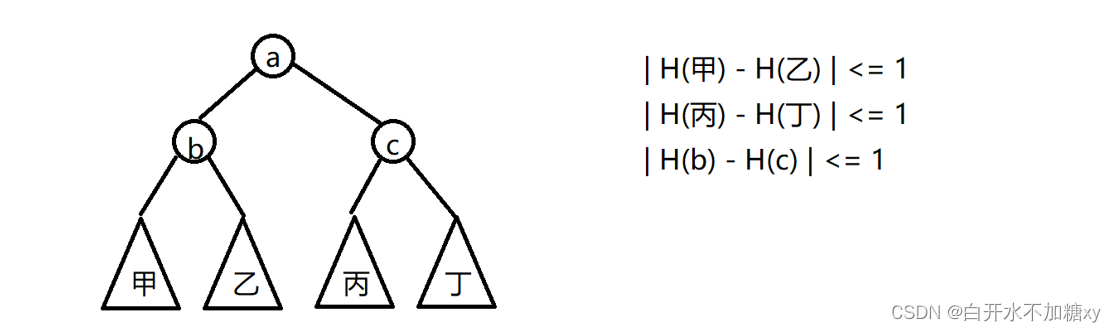
AVL中平衡(Balance)因子的定义

任取树中的结点，要求结点左子树的高度和结点右子树的高度的高度差的绝对值不能超过1
在这里插入图片描述

AVL树插入规则

1.按照普通搜索树的插入规则进行结点的插入
在这里插入图片描述
2.随着结点的插入，导致BF出现了变化，所以需要进行平衡因子的调节

没变之前的BF(parent)的值可能是?

我们这棵树插入之前，这棵树得是(MUST)是一棵AVL树->得满足AVL树的特征
-1、0、1

其中一条，任取结点，BF(结点)=-1、0、1

当BF(parent)=-1 情况时： 插入结点在parent左子树

BF(parent)=0，因此是AVL树，不需要调节平衡因子
当BF(parent)=0 情况时， 插入后平衡因子变为1或-1；变为1的情况如下所示：

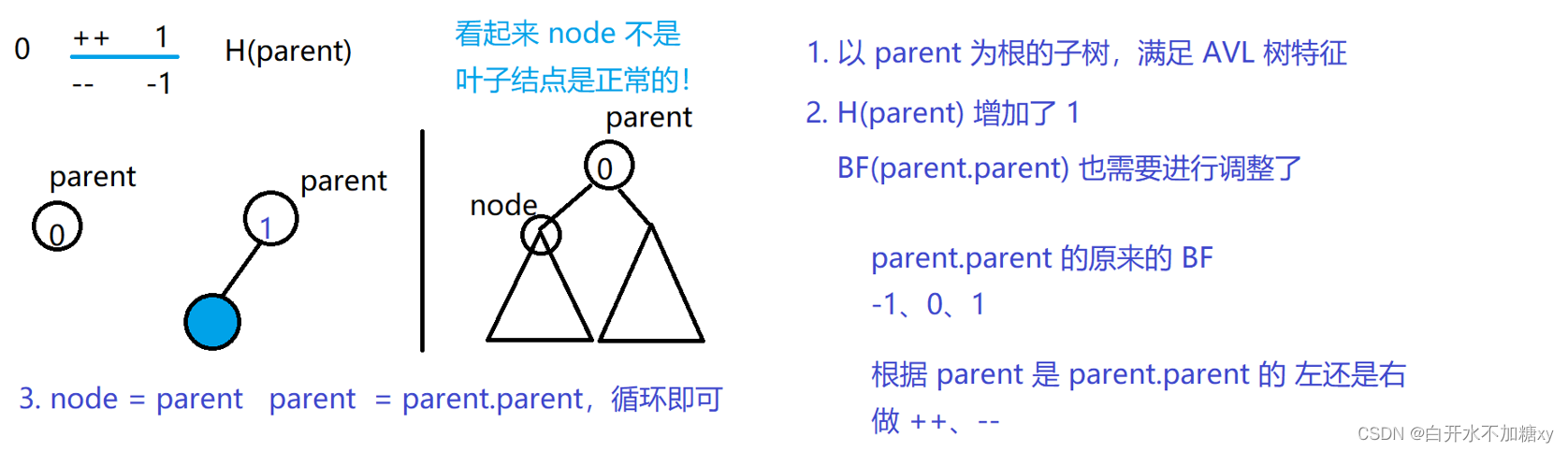
BF(parent)++，BF(parent.parent)因此++，需调整调节平衡因子（如图中3部分循环判断是否调整）。
当BF(parent)=1/-1 情况时， 插入后平衡因子变为2或-2；

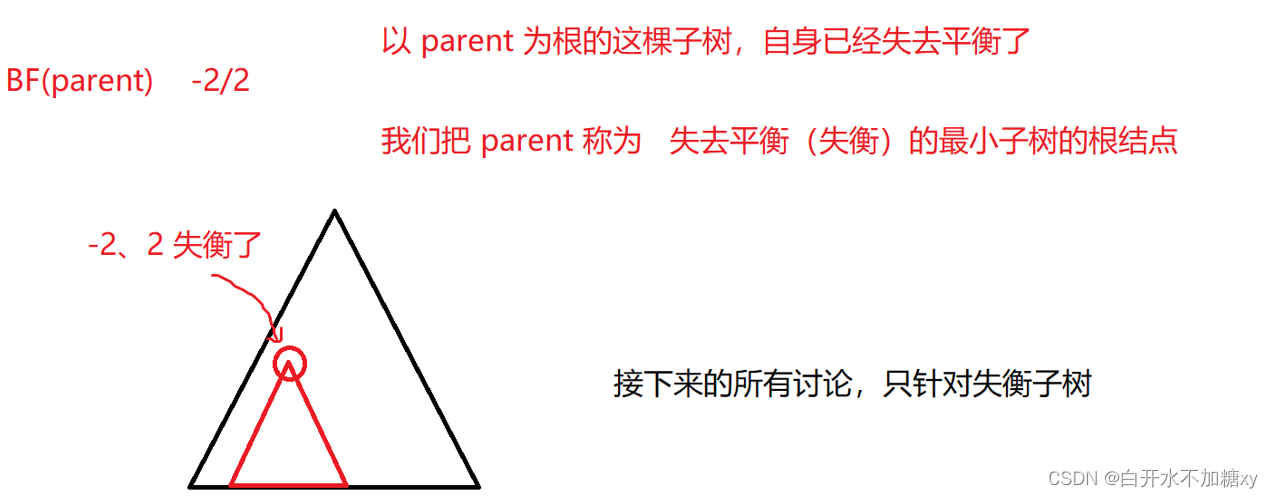
子树失衡，需要对其执行旋转操作，来调节平衡

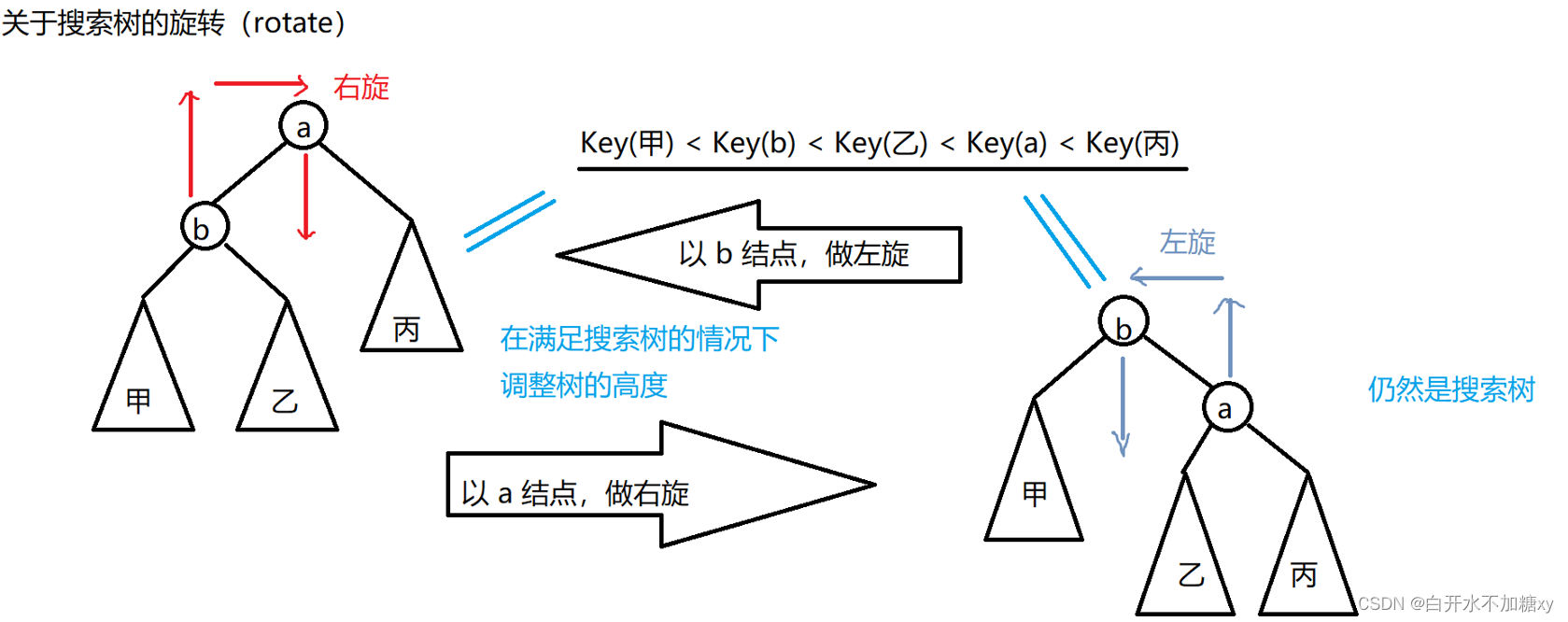
AVL树失衡情况

失衡一般为如下四种情况：

在这里插入图片描述

调整规则：

LL:对 parent做右旋，插入结束!
LR:先对node做左旋，再对parent做右旋，插入结束!RR:对 parent做左旋，插入结束!
RL:先对node做右旋，再对parent做左旋，插入结束!

左左失衡/右右失衡

失衡子树的parent不需要进行调整。右右失衡同理推导。
在这里插入图片描述
结论

左右失衡

在这里插入图片描述
假设丁的高度为x，则失衡后每个子树高度分析如下：

该分析对之后分情况讨论理解较为重要

左右失衡总共有三种

在这里插入图片描述

情况二的乙子树和丙子树的高度分析有点绕，类似反证，排除不符合整体树失衡条件的情况，得出情况二中乙丙子树高度为x、x-1;
在这里插入图片描述

其中，上述中的3小点中不平衡指的是，BF(parent),即左右失衡第一个图中的a结点。这种情况下在没插入新节点，BF(a)=2就已经失衡了，所以不符合插入失衡条件。

LR失衡三种情况总结：

在这里插入图片描述

RL失衡

RL失衡三种情况总结——类似LR画图分析

在这里插入图片描述

代码

左旋-调整平衡

通过左旋的图进行结合分析，可更利于理解代码
在这里插入图片描述

// 以 m 为结点，进行旋转
    private void leftRotate(AVLNode m) {
        // m 代表图中的 b 结点
        // parent 代表 b 结点可能存在的父亲
        AVLNode parent = m.parent;
        // right 代表图中的 a 结点
        AVLNode right = m.right;
        // leftOfRight 代表图中的可能存在的乙子树的根结点
        AVLNode leftOfRight = right.left;
        /*
        其中: m != null && right != null
        但是: parent 不保证 !null, leftOfRight 不保证 !null
         */

        right.parent = parent;  // 蓝色线的关系
        // 黑色线的关系
        if (parent == null) {
            // m 是 root
            root = right;
        } else {
            if (m == parent.left) {
                parent.left = right;
            } else {
                parent.right = right;
            }
        }

        right.left = m; // 黑色线的关系
        m.parent = right;   // 蓝色线的关系

        m.right = leftOfRight;
        if (leftOfRight != null) {
            leftOfRight.parent = m;
        }
    }

左旋单元测试测试用例

在这里插入图片描述

插入

public class AVLTree {
    public AVLNode root = null;
    public int size = 0;    // 保存树的结点个数

    public void insert(long key) {
        AVLNode node = new AVLNode();
        node.key = key;
        node.left = null;
        node.right = null;
        node.parent = null;
        node.bf = 0;

        if (root == null) {
            root = node;
            size++;
            return;
        }

        AVLNode current = root;
        AVLNode parent = null;
        while (current != null) {
            if (key == current.key) {
                return;
                //throw new RuntimeException("插入失败，key 有重复: " + key);
            } else if (key < current.key) {
                parent = current;
                current = current.left;
            } else {
                parent = current;
                current = current.right;
            }
        }

        node.parent = parent;//...............
        if (key < parent.key) {
            parent.left = node;
        } else {
            parent.right = node;
        }

        avlAdjust(parent, node);

        size++;
    }
}

调整平衡因子

private void avlAdjust(AVLNode parent, AVLNode node) {
        // parent != null && node != null

        while (true) {
            // 进行平衡因子的调整
            if (node == parent.left) {
                parent.bf++;
            } else {
                parent.bf--;
            }

            // 第一种情况
            if (parent.bf == 0) {
                return;
            }

            // 第二种情况
            if (parent.bf == -1 || parent.bf == 1) {
                node = parent;
                parent = parent.parent;

                if (parent == null) {
                    // 向上回溯到根的位置了
                    return;
                }
                continue;
            }

            // 情况三
            // parent.bf == -2 || parent.bf == 2
            break;
        }

        // 一定是出现失衡情况了
        if (parent.bf == 2) {
            if (node.bf == 1) {
                // LL 失衡
                rightRotate(parent);

                parent.bf = node.bf = 0;
            } else {
                // LR 失衡
                // node.bf == -1
                AVLNode c = node.right;
                int condition;
                if (parent.right == null) {
                    condition = 1;
                } else if (c.bf == 1) {
                    condition = 2;
                } else {
                    condition = 3;
                }

                leftRotate(node);
                rightRotate(parent);

                if (condition == 1) {
                    parent.bf = node.bf = c.bf = 0;
                } else if (condition == 2) {
                    parent.bf = -1;
                    node.bf = c.bf = 0;
                } else {
                    parent.bf = c.bf = 0;
                    node.bf = 1;
                }
            }
        } else {
            // parent.bf == -2
            if (node.bf == -1) {
                // RR 失衡
                leftRotate(parent);

                parent.bf = node.bf = 0;
            } else {
                // RL 失衡
                // node.bf == 1

                AVLNode c = node.left;
                int condition;
                if (parent.left == null) {
                    condition = 1;
                } else if (c.bf == 1) {
                    condition = 2;
                } else {
                    condition = 3;
                }

                rightRotate(node);
                leftRotate(parent);

                if (condition == 1) {
                    parent.bf = node.bf = 0;
                } else if (condition == 2) {
                    parent.bf = c.bf = 0;
                    node.bf = -1;
                } else {
                    parent.bf = 1;
                    node.bf = c.bf = 0;
                }
            }
        }
    }

AVL树正确性的验证

1.整棵树是一棵搜索树<=>中序遍历是有序的
⒉.整棵树是一棵平衡树<=>每个结点的 bf in (-1,0，1)&&每个结点的bf 计算正确

public class Main {
    public static void main(String[] args) {
        //test1();
        test2();
    }

    private static void test2() {
        for (int i = 0; i < 10; i++) {
            Random random = new Random();
            AVLTree tree = new AVLTree();
            for (int j = 0; j < 1_0000; j++) {
                int key = random.nextInt(10_0000);
                tree.insert(key);
            }

            validate(tree);
        }
    }

    private static void validate(AVLTree tree) {
        validateIsSearchTree(tree);
        validateIsBalanceTree(tree);
        System.out.println("这棵树是 AVL 树");
    }

    private static int heightAndCheckBF(AVLNode root) {
        if (root == null) {
            return 0;
        }

        int leftHeight = heightAndCheckBF(root.left);
        int rightHeight = heightAndCheckBF(root.right);

        if (root.bf != (leftHeight - rightHeight)) {
            throw new RuntimeException("有结点 bf 计算不正确");
        }

        if (root.bf != -1 && root.bf != 0 && root.bf != 1) {
            throw new RuntimeException("有结点，左右子树高度差的绝对值超过了 1，不是平衡树");
        }

        return Integer.max(leftHeight, rightHeight) + 1;
    }

    private static void validateIsBalanceTree(AVLTree tree) {
        heightAndCheckBF(tree.root);
        System.out.println("所有结点的 bf 都计算正确，并且都在范围内，是平衡树");
    }

    private static void validateIsSearchTree(AVLTree tree) {
        List<Long> inorderKeys = new ArrayList<>();
        inorderSaveKey(inorderKeys, tree.root);
        // inorderKeys 中保存的中序遍历后所有 key

        // 复制出得到的所有 key，对得到的 key 进行排序
        List<Long> keysSorted = new ArrayList<>(inorderKeys);
        Collections.sort(keysSorted);

        if (keysSorted.equals(inorderKeys)) {
            System.out.println("中序遍历是有序的，说明是搜索树");
        } else {
            throw new RuntimeException("中序遍历是无序的，说明不是搜索树");
        }
    }

    private static void inorderSaveKey(List<Long> inorderKeys, AVLNode root) {
        if (root != null) {
            inorderSaveKey(inorderKeys, root.left);
            inorderKeys.add(root.key);
            inorderSaveKey(inorderKeys, root.right);
        }
    }


    private static void test1() {
        List<Integer> list = Arrays.asList(2, 15, 8, 3, 4, 6, 9, 7, 17, 20, 19, 14);

        AVLTree tree = new AVLTree();
        for (Integer key : list) {
            tree.insert(key);
        }

        preorder(tree.root);
        System.out.println();
        inorder(tree.root);
        System.out.println();
    }

    private static void preorder(AVLNode node) {
        if (node != null) {
            System.out.printf("(%d, %d) ", node.key, node.bf);
            preorder(node.left);
            preorder(node.right);
        }
    }

    private static void inorder(AVLNode node) {
        if (node != null) {
            inorder(node.left);
            System.out.printf("(%d, %d) ", node.key, node.bf);
            inorder(node.right);
        }
    }
}