1.树的介绍以及树的基本概念和性质
2.二叉树介绍以及二叉树的性质
3.二叉树的构建:穷举创建,递归创建
4.二叉树的基本操作
之前我们介绍了顺序表,链表,以及栈和队列,这几种数据结构都属于线性结构,而我们接下来要讲的树属于非线性结构~
树的数据结构相当于一颗倒挂的树,由n个节点组成,最顶部的节点叫做根节点,最底下的节点称为叶子节点
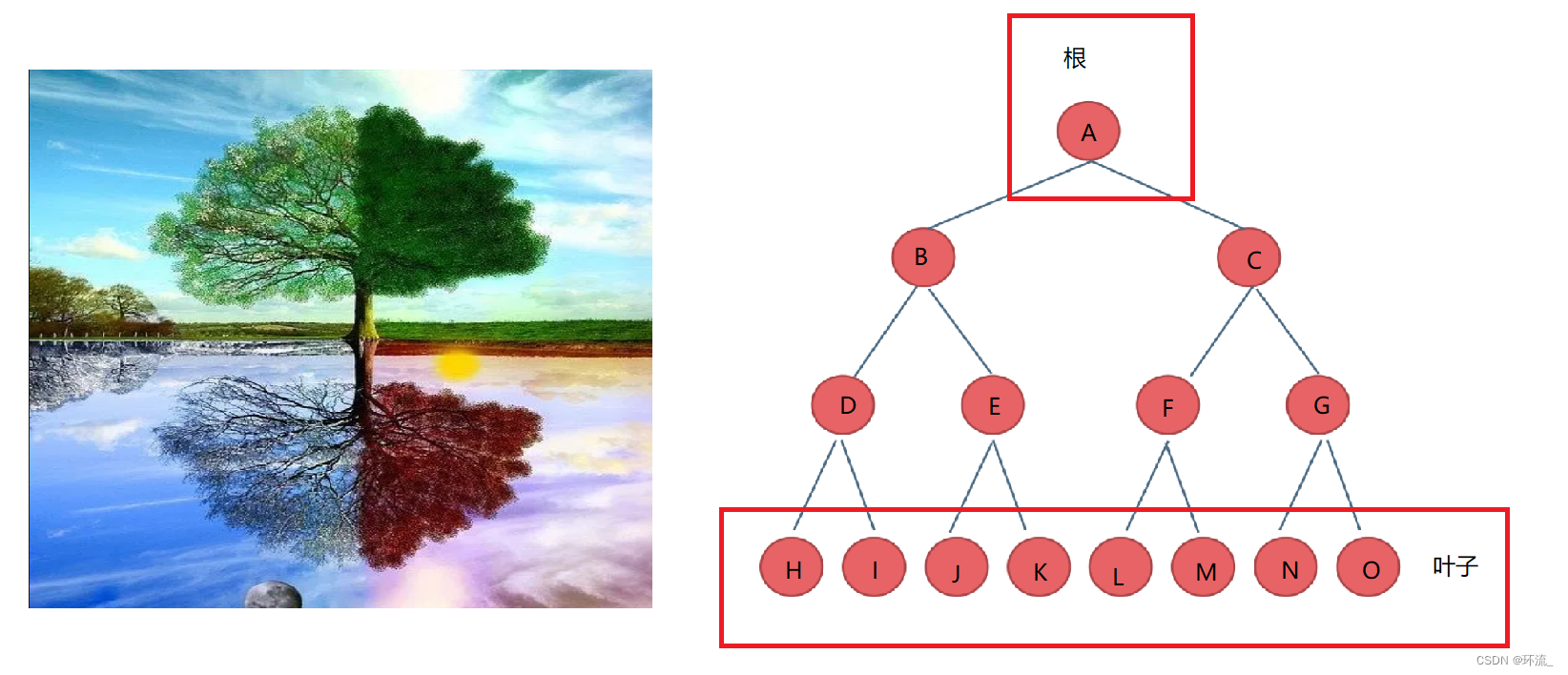
1.根节点没有前驱节点的信息
2.每个节点都包含1个或者多个节点的后继(比如说根节点A分叉为两个后继节点B和C,也就是说A节点包含B和C节点的信息)
3.树是递归实现的
一棵树包含多个子树,每个子树又有自己的根节点,比如说A节点两边是左树B和右树C,左树B两边也有左树D和右树E……以此类推

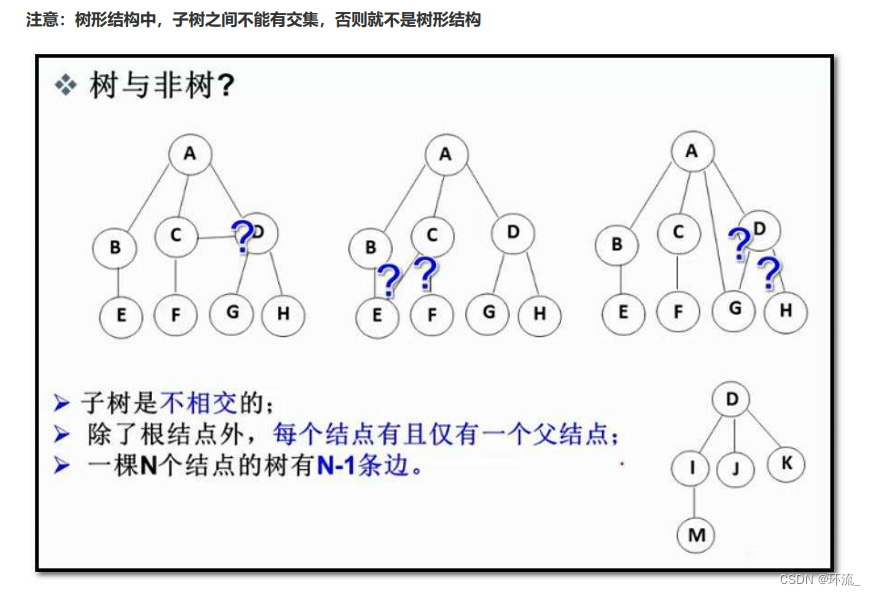
接下来来认识一下树的一些常用概念性质(结合下图来认识)
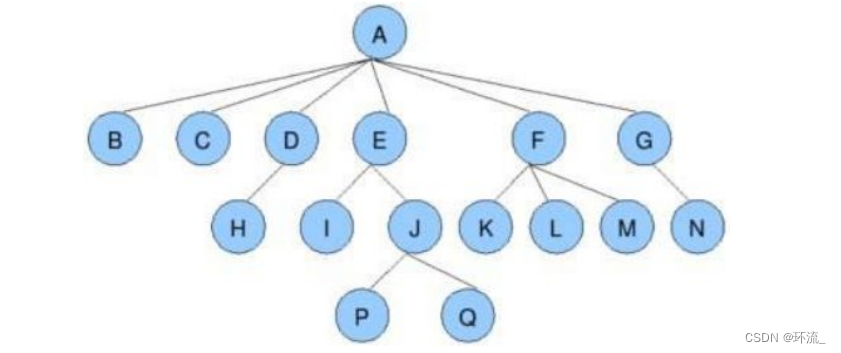
(1)结点的度:一个结点含有子树的个数称为该结点的度;简单来说就是看结点分了多少个叉,A节点分了两个叉,那么A节点的度为6,D结点的度为1,F结点的度为3……
(2)树的度:就是这一整棵树多个子树的度中的最大度,A的度为6,F的度为3……度为6是最大的,所以该树的最大度为6
(3)叶子结点(终端结点):叶子结点也叫终端结点,表示度为0的结点,度为0的结点就是该结点没有分叉,那么B,C,H,I,P,Q,K,L,M,N这些度为0的结点就统称为叶子结点
(4)父结点(双亲结点):父结点也叫做双亲结点,某个结点的前驱就是该结点的父结点,比如说B的前驱是A,那么A就是B结点的父结点,B就是A结点的子结点
(5)孩子结点(子结点):子结单就是某个结点的后继,比如A的后继有B,C,D,E,F,G 这些结点都属于A的子结点,因此!!父结点和子结点是相对而言的~
(6)根结点:一棵树中,没有双亲结点的结点;如上图:A(也就是一颗完整的树的第一个结点)
(7)结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推,因此上图这颗树一共有4层~ A在第一层,BCDEFG在第二层,HIJKLMN在第三层,PQ在第四层
(8)树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
树的以下概念只需了解,在看书时只要知道是什么意思即可:
(1)非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G...等节点为分支结点
(2)兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
(3)堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
(4)结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
(5)子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
(6)森林:由m(m>=0)棵互不相交的树组成的集合称为森林
接下来说说二叉树,二叉树才是重点
什么是二叉树?顾名思义,就是两个分叉~简单来说,二叉树的每个结点最多只能分两个叉~

棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成
意思就是说,一个空结点可以是二叉树,没有结点也可以叫二叉树,然后二叉树分为左右两棵子树,每个结点都可以分为左右两颗子树
1. 二叉树不存在度大于2的结点
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树

(图片来源:比特高博)
然后还有两种特殊的二叉树要介绍一下
(1)满二叉树:简单来说,就是除了叶子结点不分叉以外,其余的所有结点都尽它们所能分成两个叉

(2) 完全二叉树:这树的意思就是,你给一整棵树编号,同时从上到下,从左到右去数编号,结点是连在一起的

看绿框里面的两颗二叉树,第一颗是满二叉树,给它编号后,结点是完美的连起来的(从上到下,从左到右),第二棵树是完全二叉树,从1~6,也是连起来的,至于黄色框的树,本来从5要到6的,结果6没了,意思就是说,从5要到达3的左孩子结点,而不是右孩子结点,要连起来,不能空一个结点,或者说是隔着一个结点~
接下来说说二叉树的性质~(重点)

推导
(1)求第i层的结点,求不出来,但是第i层最大的结点数为 2的i-1次方
(2)求的是一整颗深度为k的二叉树的结点数最大为2的k次方-1个
(3)接下来推到一下 n0 = n2 +1 怎么来的
设结点数为N,n0为叶子结点,n1为度为1的结点,n2为度为2的结点
那么 N = n0 + n1 + n2
一颗二叉树的边为 N-1(有多少个结点,该数就有多少条-1条边)
然后度为1的结点n1提供一条边,度为2的结点n2提供两条边
因此,N-1 = n1 + 2*n2 意思就是有n1条边加上两倍n2条边,就是整棵树的边数
之后联立
1) N = n0 + n1 + n2
2) N - 1 = n1 + 2 * n2
可求得 n0 = n2 + 1;
(4)求一棵树的深度,用 log 2为底,幂为(n+1),求的的结果向上取整,意思就是说,一辆车能载10个小朋友,但是25个小朋友就要用3辆车,而不是两辆车
接下来使用枚举来创建一颗二叉树
public class BinaryTree {
static class TreeNode{
public char val;
public TreeNode left;
public TreeNode right;
public TreeNode(char val){
this.val = val;
}
}
//二叉树的根节点
public TreeNode root;
//穷举创建二叉树
public void createTree(){
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
A.left = B;
A.right = C;
B.left = D;
B.right = E;
C.left = F;
C.right = G;
E.right = H;
this.root = A;
}
//前序遍历
void preOrder(TreeNode root){
if(root == null){
return;
}
System.out.print(root.val + " ");
preOrder(root.left);
preOrder(root.right);
}
//中序遍历
void midOrder(TreeNode root){
if(root == null){
return;
}
midOrder(root.left);
System.out.print(root.val + " ");
midOrder(root.right);
}
//后序遍历
void postOrder(TreeNode root){
if(root == null){
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val + " ");
}
//获取树中节点个数(左树节点个数加上右树节点个数)
//子问题思路
int size1(TreeNode root){
int count = 0;
if(root == null){
return 0;
}else {
count++;
}
int leftNum = size1(root.left);
count += leftNum;
int rightNum = size1(root.right);
count += rightNum;
return count;
}
int size2(TreeNode root){
if(root == null) return 0;
return size2(root.left) + size2(root.right) + 1;
}
//遍历思路
public static int nodeCount;
void size3(TreeNode root){
if(root == null){
return;
}
nodeCount++;
size3(root.left);
size3(root.right);
}
/**
* 获取叶子节点个数
*/
//子问题思路
int getLeafNodeCount1(TreeNode root){
int count = 0;
if(root == null){
return 0;
}else if(root.left == null && root.right == null){
count++;
}
int leftCount = getLeafNodeCount1(root.left);
count += leftCount;
int rightCount = getLeafNodeCount1(root.right);
count += rightCount;
return count;
}
//遍历思路
public static int leafCount;
void getLeafCount(TreeNode root){
if(root == null){
return;
}
if(root.left == null && root.right == null){
leafCount++;
}
getLeafCount(root.left);
getLeafCount(root.right);
}
/**
* 获取第k层节点个数
*/
int KCount(TreeNode root, int k){
int count = 0;
if(root == null){
return 0;
}
if(k == 1){
count++;
}
int left = KCount(root.left,k-1);
count += left;
int right = KCount(root.right,k-1);
count += right;
return count;
}
int KCount2(TreeNode root, int k){
if(root == null) return 0;
if(k == 1){
return 1;
}
return KCount2(root.left, k-1) + KCount2(root.right,k-1);
}
/**
* 获取树的高度
*/
int Height(TreeNode root){
if(root == null) return 0;
return Math.max(Height(root.left),Height(root.right)) + 1;
}
/**
* 遍历看看树中是否存在value值
*/
TreeNode find(TreeNode root, char key){
if(root == null) return null;
if(root.val == key){
return root;
}
TreeNode ret1 = find(root.left, key);
if(ret1 != null){
return ret1;
}
TreeNode ret2 = find(root.right, key);
if(ret2 != null){
return ret2;
}
return null;
}
public boolean isBalanced(TreeNode root) {
if(root == null) return true;
return maxDepth(root) >= 0;
}
public int maxDepth(TreeNode root) {
if(root == null) return 0;
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
if(leftHeight >= 0 && rightHeight <= 0 && Math.abs(leftHeight-rightHeight) <= 1){
return Math.max(leftHeight,rightHeight) + 1;
}else {
return -1;
}
}
//层序遍历
void levelOrder(TreeNode root){
if(root == null) return;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
TreeNode cur = queue.poll();
System.out.print(cur.val + " ");
if(cur.left != null){
queue.offer(cur.left);
}
if(cur.right != null){
queue.offer(cur.right);
}
}
}
}遍历分为4种遍历,都是用递归写的
前序遍历:根左右
中序遍历:左根右
后序遍历:左右根
层序遍历:从上到下,从左到右,依次读取






![[附源码]Python计算机毕业设计房屋租赁系统](https://img-blog.csdnimg.cn/660b44d5759d4060870f33e5ebb6aa5b.png)