121. 买卖股票的最佳时机

自己的思路：采用求最长连续子串和题目的思路

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 1) return 0;
        int[] nums = new int[prices.length - 1];
        for(int i = 0;i < prices.length - 1;i++){
            nums[i] = prices[i + 1] - prices[i];
        }
        int[] dp = new int[prices.length - 1];
        dp[0] = nums[0];
        int res = nums[0];
        for(int i = 1;i < dp.length;i++){
            dp[i] = Math.max(dp[i-1] + nums[i],nums[i]);
            res = Math.max(dp[i],res);
        }
        return res < 0 ? 0:res;
    }
}

贪心思路：

class Solution {
    public int maxProfit(int[] prices) {
        int low = Integer.MAX_VALUE;
        int result = 0;
        for(int i = 0;i < prices.length;i++){
            low = Math.min(low,prices[i]);
            result = Math.max(result,prices[i] - low);
        }
        return result;
    }
}

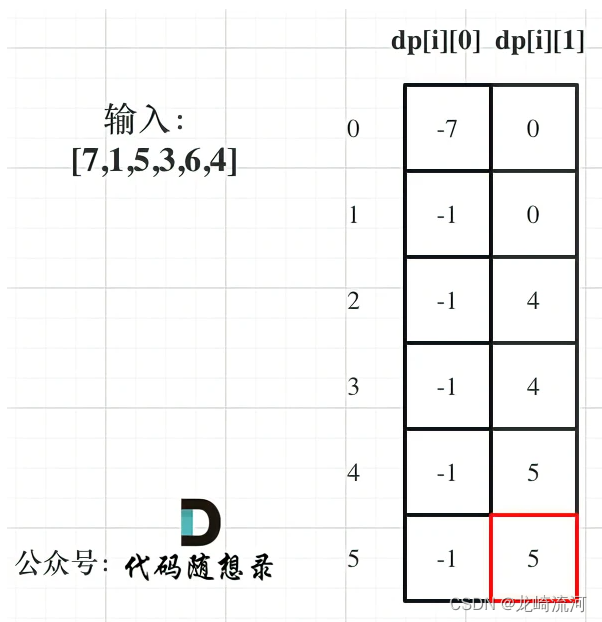
dp[i][0] dp[i][1] 表示第i天持有股票所得最多现金.
持有股票dp[i][0]：
1.之前就持有股票dp[i - 1][0]
2.现在刚持有也就是买入股票-prices[i]
不持有股票dp[i][1]:
1.之前就不持有股票dp[i - 1][1]
2.现在刚不持有也就是卖掉股票dp[i - 1][0] + prices[i]

class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length == 0) return 0;
        int length = prices.length;
        int[][] dp = new int[length][2];
        int result = 0;
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < length; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
            dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1]);
        }
        return dp[length - 1][1];
    }
}

优化空间复杂度，不需要那么长的数组只需要两块。

class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length == 0) return 0;
        int length = prices.length;
        int[] dp = new int[2];
        int result = 0;
        dp[0] = -prices[0];
        dp[1] = 0;
        for (int i = 1; i < length; i++) {
            dp[0] = Math.max(dp[0], -prices[i]);
            dp[1] = Math.max(dp[0] + prices[i], dp[1]);
        }
        return dp[1];
    }
}

122. 买卖股票的最佳时机 II

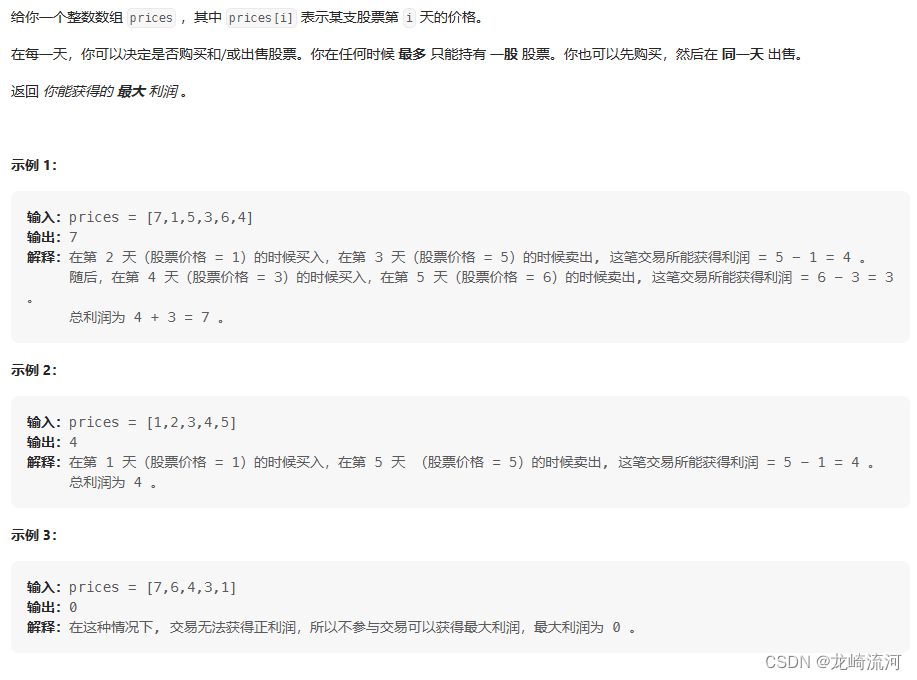
贪心算法：

class Solution {
    public int maxProfit(int[] prices) {
        if(prices.length == 1) return 0;
        int[] nums = new int[prices.length - 1];
        for(int i = 0;i < prices.length - 1;i++){
            nums[i] = prices[i + 1] - prices[i];
        }
        int result = 0;
         for(int i = 0;i < nums.length;i++){
             if(nums[i] > 0){
                 result += nums[i];
             }
         }
        return result;
    }
}

而本题，因为一只股票可以买卖多次，所以当第i天买入股票的时候，所持有的现金可能有之前买卖过的利润。

那么第i天持有股票即dp[i][0]，如果是第i天买入股票，所得现金就是昨天不持有股票的所得现金 减去 今天的股票价格 即：dp[i - 1][1] - prices[i]。
dp[i-1][1] - price[i]是之前之前买卖过的利润 再减去当前买入

// 优化空间
class Solution {
    public int maxProfit(int[] prices) {
        int[] dp = new int[2];
        // 0表示持有，1表示卖出
        dp[0] = -prices[0];
        dp[1] = 0;
        for(int i = 1; i <= prices.length; i++){
            // 前一天持有; 既然不限制交易次数，那么再次买股票时，要加上之前的收益
            //与上一题唯一不同点
            dp[0] = Math.max(dp[0], dp[1] - prices[i-1]);
            // 前一天卖出; 或当天卖出，当天卖出，得先持有
            dp[1] = Math.max(dp[1], dp[0] + prices[i-1]);
        }
        return dp[1];
    }
}

123. 买卖股票的最佳时机 III

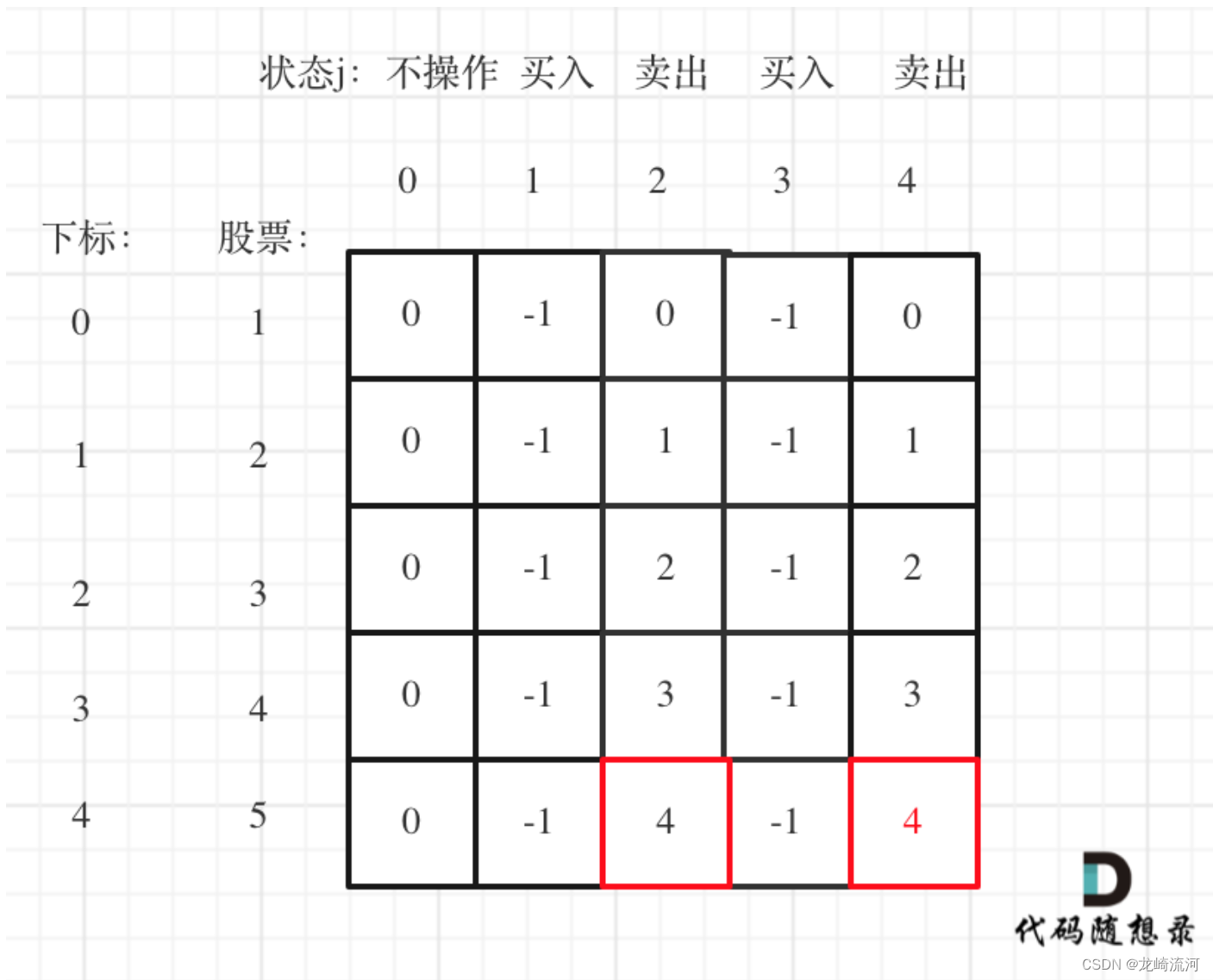
class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        if(len == 0) return 0;
        int[][] dp = new int[len][5];
        dp[0][1] -= prices[0];
        dp[0][3] -= prices[0];
        for(int i = 1;i < prices.length;i++){
            dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
            dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1]+prices[i]);
            dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2]-prices[i]);
            dp[i][4] = Math.max(dp[i-1][4],dp[i-1][3]+prices[i]);
        }
        return dp[len - 1][4];
        }
}

class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        if(len == 0) return 0;
        int[] dp = new int[5];
        dp[1] -= prices[0];
        dp[3] -= prices[0];
        for(int i = 1;i < len;i++){
            dp[1] = Math.max(dp[1],dp[0]-prices[i]);
            dp[2] = Math.max(dp[2],dp[1]+prices[i]);
            dp[3] = Math.max(dp[3],dp[2]-prices[i]);
            dp[4] = Math.max(dp[4],dp[3]+prices[i]);
        }
        return dp[4];
        }
}

188. 买卖股票的最佳时机 IV

和上一题思路一致

class Solution {
    public int maxProfit(int k, int[] prices) {
        int[] dp = new int[2*k + 1];
        for(int i = 0;i < 2*k + 1;i++){
            if(i % 2 == 1){
                dp[i] = -prices[0];
            }
        }
        for(int i = 0;i < prices.length;i++){
            for(int j = 1;j < 2*k+1;j++){
                int temp = j % 2 == 1?-prices[i]:prices[i];
                dp[j] = Math.max(dp[j],dp[j-1]+temp);
            }
        }
        return dp[2*k];
    }
}