【数据结构】堆排序

news2024/11/26 23:26:01

堆是一种叫做完全二叉树的数据结构，可以分为大根堆，小根堆，而堆排序就是基于这种结构而产生的一种程序算法。

大堆：每个节点的值都大于或者等于他的左右孩子节点的值

小堆：每个结点的值都小于或等于其左孩子和右孩子结点的值

不管是大堆还是小堆父节点的数组下标和其孩子节点的下标关系都为

parent=(child-1)/2 leftchild=2*parent+1 rightchild=2*parent+2

建堆

建堆有两种方法1.向上调整建堆2.向下调整建堆

向上调整建堆

void Swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}
void AdjustUp(int* a, int child)     //向上调整
{
    int parent = (child - 1) / 2;

    while (child > 0)
    {
        if (a[child] < a[parent])    //建大堆还是小堆在这里调整
        {                            //大堆a[parent]<a[child] 小堆反之
            Swap(&a[child], &a[parent]);
            child = parent;
            parent = (child - 1) / 2;

        }

        else
        {
            break;
        }
    }
}

void HeapSort(int* a, int n)
{
    for (int i = 0; i < n; ++i)
    {
        AdjustUp(a, i);
    }
}

int main()
{
    int a[] = { 1,10,2,20,3,30,4,40,5,50 };
    HeapSort(a, sizeof(a) / sizeof(int));

    for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
    {
        printf("%d ", a[i]);
    }

    return 0;
}

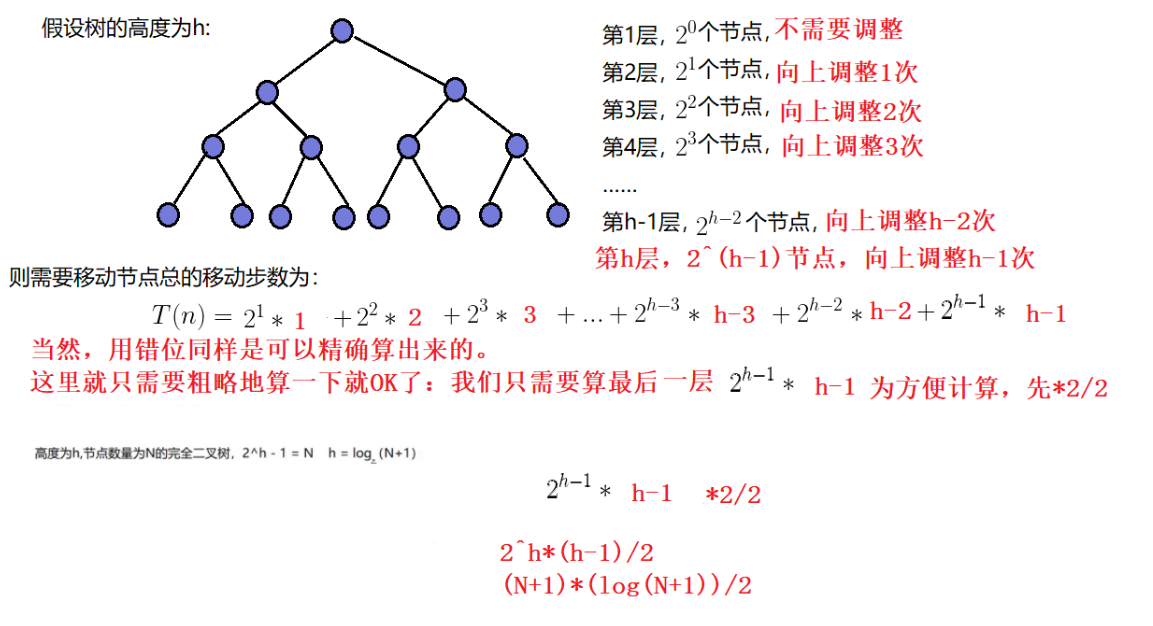
向上调整建堆是从数组的第一个元素开始一次向后遍历数组元素，每一个数组元素都向上调整建堆，这个过程就模拟建立起了堆，这个过程的时间复杂度推导过程：O(N*logN)

2.向下调整建堆（推荐使用）

void Swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}
void AdjustDown(int* a, int n, int parent)     //向下调整
{
    int minChild = parent * 2 + 1;
    while (minChild < n)
    {
        if (minChild + 1 < n && a[minChild + 1] > a[minChild])   //这里控制大小堆
        {
            minChild++;

        }

        if (a[minChild] > a[parent]) //这里控制大小堆
        {
            Swap(&a[minChild], &a[parent]);
            parent = minChild;
            minChild = parent * 2 + 1;

        }
        else
        {
            break;
        }

    }


}
void HeapSort(int* a, int n)
{
    for (int i = (n - 1-1) / 2; i >= 0; --i)
    {
        AdjustDown(a, n, i);
    }
}

int main()
{
    int a[] = { 1,10,2,20,3,30,4,40,5,50 };
    HeapSort(a, sizeof(a) / sizeof(int));

    for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
    {
        printf("%d ", a[i]);
    }

    return 0;
}

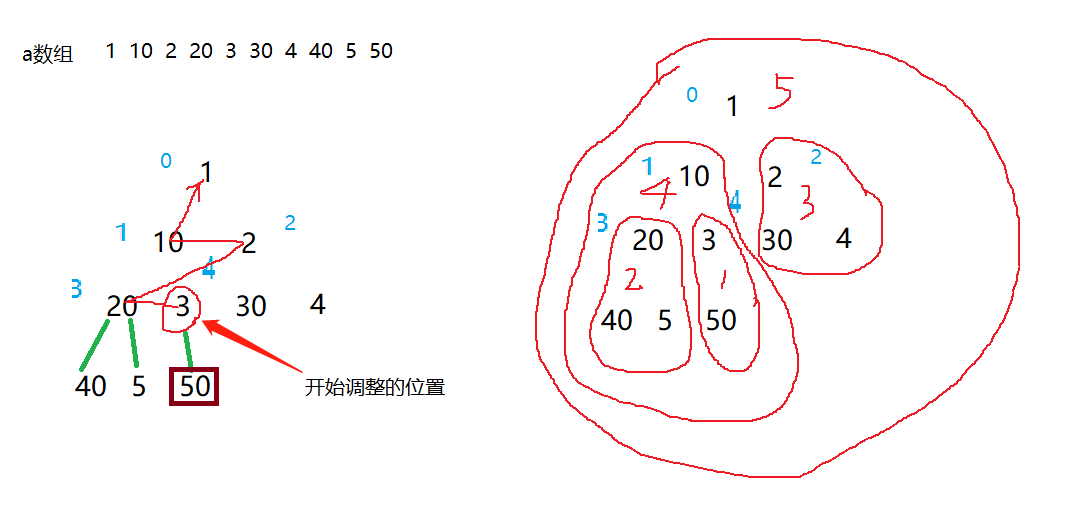
向下调整的开始的位置是最后一个元素的父节点位置，因为最后一行的元素本来就符合大堆或者小堆的性质所以不用调整，根据数组的最后一个元素的下标计算出该节点的父节点的数组下标，从这个父节点开始向下调整，调整完后再将父节点的数组下标--，再从这个节点开始向下调整，直到调整完根节点后调整结束，堆就建立好了，大小堆是根据向下调整函数里的比较决定的。时间复杂度推导如下O(N)：

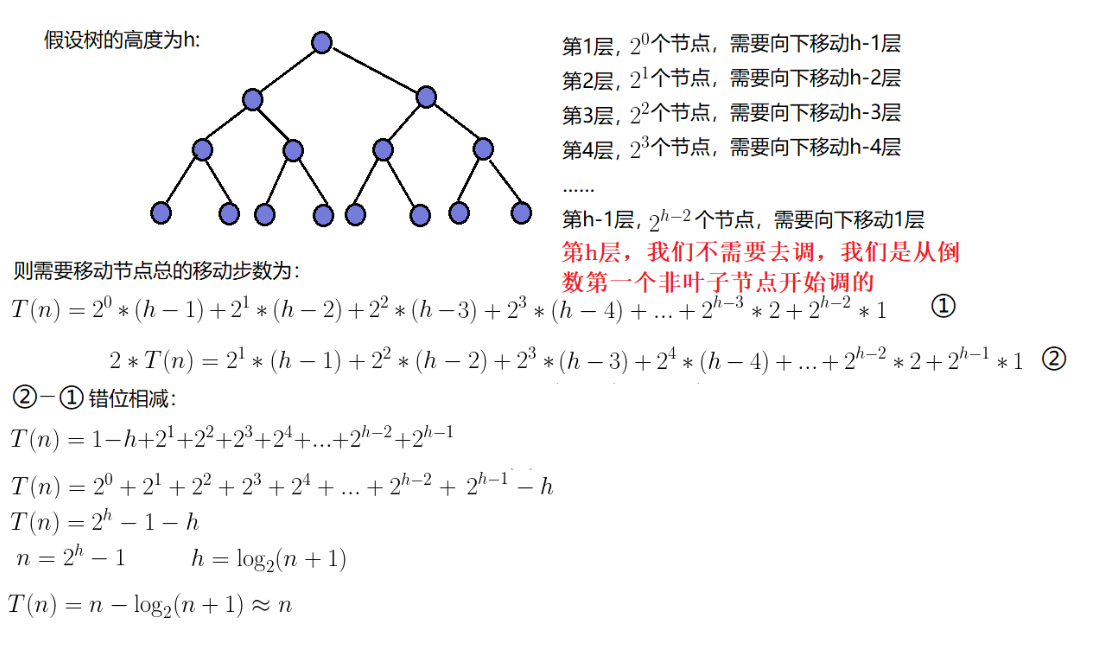
因为向下调整的时间复杂度低于向上调整的时间复杂度，所以推荐使用的是向下调整建堆。

2.选数

了解完以后，我们来实现堆排序：

void AdjustDown(HPDataType* a, int n, int parent)
{
    //最小的默认为左孩子
    int minchild = 2 * parent + 1;
    while (minchild <n)
    {
        //找出小的那个孩子
        if (minchild+1<n&&a[minchild+1] < a[minchild])
        {
            minchild++;
        }
        //小堆
        if (a[minchild] < a[parent])
        {
            Swap(&a[minchild], &a[parent]);
            parent = minchild;
            minchild = 2 * parent + 1;
        }
        else
        {
            break;
        }
    }
}

void HeapSort(int* a, int n)
{
    
    for (int i = (n-1-1)/2; i>=0; i--)
    {
        AdjustDown(a, n, i);
    }
    //选数
    int i = 1;
    while (i < n)
    {
        Swap(&a[0], &a[n - i]);
        AdjustDown(a, n - i, 0);
        i++;
    }

}


int main()
{
    int a[] = { 15,1,19,25,8,34,65,4,27,7 };
    HeapSort(a, sizeof(a) / sizeof(int));

    for (int i = 0; i < sizeof(a) / sizeof(int); i++)
    {
        printf("%d ", a[i]);
    }
    printf("\n");
    return 0;
}

这里的思路就是先对数组进行向下调整建堆，如果要升序就建立大堆，将根节点位置的元素和最后一个元素交换位置使得最大的元素放到了数组的最后边，放到后边的元素不参与向下调整（通过传参控制），然后让被换到根节点的元素向下调整，回到符合堆的性质的位置，此时调整完成后次大的元素被调整到了根节点的位置，再让根节点的元素和倒数第二个元素交换，交换到后边的元素不参与向下调整，再次进行向下调整，直到i=n时结束调整，此时输出数组就是升序的。如果要降序那就建立小堆。

总结一句话：

升序--建大堆，降序--建小堆

3.TOP-K问题

如何从数组中找到前K个大或者前K个小的数？

错误的思维：

选前K个大的数建立的是大堆，那最大的元素就在最上方，我们拿走了最大的元素，那剩下的元素堆的关系全乱了，又得重新排序，再选出最大的元素，这样一来假设要从特别大的一堆数据中进行选数那代价就非常大了，效率变得很低。同理选小数不能建小堆。

正确方法：

用数据集合中前K个元素来建堆

前k个最大的元素，则建小堆

前k个最小的元素，则建大堆

用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

代码实现：

#include<stdlib.h>
#include<stdio.h>


void Swap(int* p1, int* p2)
{
    int tmp = *p1;
    *p1 = *p2;
    *p2 = tmp;
}


void AdjustDown(int* a, int n, int parent)     //向下调整
{
    int minChild = parent * 2 + 1;
    while (minChild < n)
    {
        if (minChild + 1 < n && a[minChild + 1] < a[minChild])
        {
            minChild++;

        }

        if (a[minChild] < a[parent])
        {
            Swap(&a[minChild], &a[parent]);
            parent = minChild;
            minChild = parent * 2 + 1;

        }
        else
        {
            break;
        }

    }


}
void Topk(int* a, int k,int n)
{
    int* minheap = (int*)malloc(k * sizeof(int));
    if (minheap == NULL)
    {
        perror("malloc fail!");
        exit(-1);
    }

     for (int i = 0; i < k; i++)
    {
        minheap[i] = a[i];
    }

    for (int j = (k - 2) / 2; j >= 0; --j)
    {
        AdjustDown(minheap, k, j);   //向下调整建小堆因为选的是前K大的数 ---如果选小数就建大堆
    }

    int k1 = k;

    //遍历k后的元素交换然后调整
    while (k <n)
    {
        if (a[k] > minheap[0])
        {
            minheap[0] = a[k];
            AdjustDown(minheap, k, 0);

        }
        ++k;
    }


    for (int i = 0; i < k1; ++i)
    {
        printf("%d ", minheap[i]);
    }

}
int main()
{
    int a[] = { 1,10,2,20,3,30,4,40,5,50 };
    int k = 5;  //选出前5个大的数
    int n = sizeof(a) / sizeof(int);  //数组元素个数
    Topk(a, k,n);
    

    return 0;
}