一. MIMO信道估计的重要性

二. 最经典的两种信道估计方法

2.1 最小二乘信道估计(LS)

2.2 最小均方误差信道估计(MMSE)

三. 优化传统的MIMO信道估计技术

四. 介绍压缩感知技术

五. 基于压缩感知的MIMO信道估计

5.1 压缩感知怎么用在MIMO信道估计

5.2 改进压缩感知用在信道估计

六. 如何利用时间相关性估计MIMO信道

6.1 介绍贝叶斯再信道估计中的用途

6.2 基于时间相关性的MIMO相关性

七. 基于高速移动的MIMO信道估计

八. 基于混合模数的MIMO信道估计

九. 基于低分辨率模数转换器的MIMO信道估计

9.1 介绍克拉-美罗界

9.2 基于低分辨率的模数转换器

十. 基于透镜天线阵列的MIMO信道估计

十一. 基于神经网络的MIMO信道估计

总结

（1）细节总结

（2）合法端优化MIMO信道估计的方向

首先本篇文章会使用到的通信领域常用缩略语如下：

CSI	Channel State Information	信道状态信息
LS	Least Square	最小二乘信道估计
MMSE	Minimum Mean Square Error	最小均方误差信道估计
MSE	Mean Square Error	均方误差
CS	Compressive Sensing	压缩感知
HAD	Hybrid Analog Digital	混合模数
ADCs	Analog-to-Digital	模数转换器
ARIMA	Autoregressive Integrated Moving Average Model	差分自回归移动平均模型
ADF	Augmented Dickey Fuller	单位根检验
AIC	Akaike Information Criterion	赤池信息准则

一. MIMO信道估计的重要性

是否获得精确CSI，将影响着发射机的波束赋形和接收机的解码精度。一方面，电磁波在复杂的无线信道中传播会经历直射、反射、折射以及散射等过程，产生多径衰落，为了正确检测出传输信号，接收机需要利用信道估计补偿接收信号；另一方面，基站需要根据信道估计实现波束赋形，对发送信号进行预处理，使其空间的分布特性与当前的信道条件相匹配，以充分获得大规模MIMO技术带来的阵列增益。

经典的MIMO信道估计方法是利用导频信号：

• 最小二乘信道估计 ：复杂度低，估计精度一般；

• 最小均方误差信道估计 ：精度相对高，但需要信道相关矩阵和噪声方差作为先验信息，导致计算复杂度高；

当通信环境具有丰富的散射体时，CSI协方差矩阵满秩，大规模MIMO的信道状态信息的估计开销将会很大。

二. 最经典的两种信道估计方法

2.1 最小二乘信道估计(LS)

有关最小二乘信道估计的推导，我就直接用PPT展示了，简洁明了。

2.2 最小均方误差信道估计(MMSE)

这个地方也直接上PPT了

三. 优化传统的MIMO信道估计技术

[HLY+19]基于LS估计器和稀疏消息传递算法的稀疏信道估计技术。该稀疏信道估计技术迭代地用稀疏消息传递算法来检测毫米波大规模MIMO稀疏信道中较大信道系数的位置，然后用LS估计器估计非零项的值，可以取得较高的信道估计精度。

[YZG+20]首先利用LS估计器获得初始CSI，然后利用图数据结构对所获得的CSI进行表征，并通过图边缘的权值来描述信道的空间相关性，最终提出基于图神经网络的大规模MIMO信道追踪技术（优于前馈神经网络）。

[HLY+19] C. Huang, L. Liu, C. Yuen, and S. Sun. Iterative channel estimation using LSE and sparse message passing for MmWave MIMO systems [J]. IEEE Transactions on Signal Processing, 2019, 67(1): 245–249.

[YZG+20]Y. Yang, S. Zhang, F. Gao, J. Ma, and O. A. Dobre. Graph neural network-based channel tracking for massive MIMO networks [J]. IEEE Communications Letters, 2020, 24(8): 1747–1751.

四. 介绍压缩感知技术

奈奎斯特采样定理要求采样频率必须大于信号中最高频率的两倍。直到有一天，这个定律有了新的世界：

陶哲轩等人指出独立同分布的高斯随机测量矩阵可以成为普适的压缩感知测量矩阵。

先看看信号重建领域怎么解释：如果一个信号在某个变换域是稀疏的，那么就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上，然后通过求解一个优化问题就可以从这些少量的投影中以高概率重构出原信号。

再看看通信人怎么说：大规模MIMO的信道具有稀疏性，压缩感知的重建过程，也就是MIMO信道估计的过程，本质是求解欠定方程组𝑦=𝜃𝑆y=θS，这是一个零范数最小化问题，是一个NP完全类问题。所以通信领域通常转化为1范数最小化求解，或者使用一些近似估计算法。

备注：陶哲轩是华人，现在是澳大利亚国籍，16岁念完本科，17岁一年的时间读完硕士，20岁拿到普林斯顿大学博士学位，24岁成为加州大学终生教授.

欠定方程组：变量数多于方程数。

L0范数：向量中非零元素的个数。L1范数：向量元素的绝对值求和。

五. 基于压缩感知的MIMO信道估计

5.1 压缩感知怎么用在MIMO信道估计

为什么MIMO信道是稀疏的：大规模MIMO使用高频率信号（通常30GHz~300GHz的毫米波），该信道具有很大的路径损耗，其在波束空间只有少数具有大增益的传播路径，称之为MIMO信道的稀疏性。

举一个论文的例子：[GGL16]提出具有稳健性能的分块压缩采样匹配追踪信道估计技术。该信道估计技术利用信道角域的块结构稀疏性，进一步改进大规模MIMO系统的信道估计性能。

[GGL16] Q. Guo, G. Gui, and F. Li. Block-partition sparse channel estimation for spatially correlated massive MIMO systems [C]. 2016 8th International Conference on Wireless Communications and Signal Processing (WCSP), 2016: 1-4.

出现的问题以及如何解决：基于CS的MIMO信道估计大多面临着网格不匹配问题(网格不匹配会出现功率泄露问题），后续发现原子范数去噪算法可一定程度解决此问题。与基于网格的CS算法相比，原子范数算法不需要将到达角和出发角的角度空间离散到网格中，所以可解决网格不匹配问题，而且信道估计精度更高。

5.2 改进压缩感知用在信道估计

同样举几个论文例子：

[GHD+16]提出了一个基于分布式压缩感知的信道估计方案，采用自适应测量矩阵的网格匹配跟踪策略，解决了离散到达角和出发角引起的功率泄露问题。

[WXT17]将原子范数去噪算法应用于信道估计，实现了毫米波MIMO信道的高精度估计。但由于大规模MIMO信道维度很大，原子范数去噪算法具有很慢的信道估计技术。[TZW18]发现可以利用乘数交替方向法来加速信道估计。

[WGS+20]提出了一种可以对连续到达角、时延和复杂增益进行联合估计的移位不变块稀疏性信道估计技术。 [JGT19]针对宽带毫米波大规模MIMO系统，利用去网格的稀疏贝叶斯学习技术对连续到达方向和时延进行超分辨率估计，该技术具有较好的信道估计精度。

[GHD+16]Z. Gao, C. Hu, L. Dai, and Z. Wang. Channel estimation for millimeter-wave massive MIMO with hybrid precoding over frequency-selective fading channels [J]. IEEE Communications Letters, 2016, 20(6): 1259–1262.

[WXT17] Y. Wang, P. Xu, and Z. Tian. Efficient channel estimation for massive MIMO systems via truncated two-dimensional atomic norm minimization [C]. 2017 IEEE International Conference on Communications (ICC), 2017: 1–6.

[TZW18] Y. Tsai, L. Zheng, and X. Wang. Millimeter-wave beamformed full-dimensional MIMO channel estimation based on atomic norm minimization [J]. IEEE Transactions on Communications, 2018, 66(12): 6150–6163.

[WGS+20] M. Wang, F. Gao, N. Shlezinger, M. F. Flanagan, and Y. C. Eldar. A block sparsity based estimator for mm Wave massive MIMO channels with beam squint [J]. IEEE Transactions on Signal Processing, 2020, 68

[JGT19] M. Jian, F. Gao, Z. Tian, S. Jin, and S. Ma. Angle-domain aided UL/DL channel estimation for wideband mm Wave massive MIMO systems with beam squint [J]. IEEE Transactions on Wireless Communications, 2019, 18(7): 3515–3527.

六. 如何利用时间相关性估计MIMO信道

6.1 介绍贝叶斯再信道估计中的用途

6.2 基于时间相关性的MIMO相关性

利用CSI的时间相关性，可以从历史时隙的CSI中获得当前时隙的CSI的部分信道支持信息。举几个论文例子：

[LLD16]利用大规模MIMO信道的块稀疏结构，提出了辅助信道估计技术，采用了突发最小绝对收缩与选择运算算法。该算法可以缓解传统压缩感知算法对鲁棒性的严格稀疏要求，同时减少了基站获取下行CSI的导频开销和反馈开销。

为了解决大规模MIMO系统中下行信道获取问题， [HLW+19]利用上行链路和下行链路之间的部分互易性来减少训练和反馈开销。该论文提出一种增强的牛顿正交匹配追踪算法，从上行链路中提取与频率无关的参数包括下倾角、方位角和延迟。然后利用这些频率无关参数的信息，利用eNOMP算法可以精确估计下倾角、方位角和延迟，利用重建的多用户下行信道可以实现较高的和速率。

[CSL17]设计了一种高斯混合先验模型，该模型能够有效地捕获每个信道矩阵的稀疏性和不同用户信道矩阵共享的部分联合稀疏性。利用该稀疏性，该论文提出了一种变分期望最大化策略来估计高斯混合先验模型和信道矩阵相关的超参数。

[LLD16] A. Liu, V. K. N. Lau, and W. Dai. Exploiting burst-sparsity in massive MIMO with partial channel support information [J]. IEEE Transactions on Wireless Communications, 2016, 15(11): 7820–7830.

[HLW+19] Y. Han, Q. Liu, C. K. Wen, S. Jin, and K. K. Wong. FDD massive MIMO based on efficient downlink channel reconstruction [J]. IEEE Transactions on Communications, 2019, 67(6): 4020–4034.

[CSL17] X. Cheng, J. Sun, and S. Li. Channel estimation for FDD multi-user massive MIMO : a variational bayesian [J]. IEEE Transactions on Wireless Communications, 2017, 16(11): 7590–7602.

七. 基于高速移动的MIMO信道估计

在高速列车和无人机通信等应用中，MIMO基站或用户会高速移动，信道的相干时间变短，信道准静态假设会失效。举几个论文的例子：

[MZL+19]提出了一种基于期望最大化的稀疏贝叶斯学习框架来学习时变大规模MIMO信道模型的时空参数，并采用降维卡尔曼滤波进行信道追踪。

[XXZ+20]发现MIMO角域信道表现出两种时空稀疏结构，分别是时间共同稀疏结构和空间聚类稀疏结构。利用该信道的时空稀疏结构，该论文提出一种新的结构化变分贝叶斯推理框架，用于导频传输阶段的信道估计。同时在不增加导频消耗的情况下，进一步提出在数据传输阶段基于数据辅助的信道预测方案，该方案解决了信道时变问题。

[LHC20]利用信道的时间相关性、空间相关性和频率相关性，将频域和时域的所有天线对之间的CSI数据视为一个四维张量作为深度神经网络的输入，其中，卷积层用于模拟CSI在空间和频率域的非导频位置的插值过程，长短期记忆层用于学习数据的时间相关性并进行CSI预测。由此，构建了一个解决高速移动场景下大规模MIMO信道估计问题的深度神经网络。

[MZL+19]J. Ma, S. Zhang, H. Li, F. Gao, and S. Jin. Sparse bayesian learning for the time-varying massive MIMO channels: acquisition and tracking [J]. IEEE Transactions on Communications, 2019, 67(3): 1925–1938.

[XXZ+20] X. Xia, K. Xu, S. Zhao, and Y. Wang. Learning the time-varying massive mimo channels: robust estimation and data-aided prediction [J]. IEEE Transactions on Vehicular Technology, 2020, 69(8): 8080–8096.

[LHC20]Y. Liao, Y. Hua, and Y. Cai. Deep learning based channel estimation algorithm for fast time-varying MIMO-OFDM systems [J]. IEEE Communications Letters, 2020, 24(3): 572–576.

八. 基于混合模数的MIMO信道估计

基站的每个天线都要单独与射频链路集成，对大规模MIMO系统在硬件结构上复杂度极高，同时电路能耗很高。研究工作发现可以将混合模数结构用在大规模MIMO收发器上，通过平衡模拟射频和数字基带部分来减少射频链的数量。

减少射频链的数量带来的优点：降低大规模MIMO设计复杂度；

减少射频链的数量带来的缺点：信道估计变难，基带信道估计起只能通过几个射频链路获得压缩的信道表示。

举两个论文例子：

[LGL16]基于参数化信道模型，采用基于网格的正交匹配追踪算法进行信道参数估计。在三维大规模MIMO信道中，其在波束域信道向量中存在两种稀疏结构：均匀面阵中子阵列之间的公共稀疏结构，每个子阵列内部的块稀疏结构。

[WLX+19]提出一种新的结构化稀疏贝叶斯学习框架进行HAD结构下三维大规模MIMO信道估计（优化原始贝叶斯MIMO信道估计）。

九. 基于低分辨率模数转换器的MIMO信道估计

9.1 介绍克拉-美罗界

在估计信道参数时，根据已有信息得到似然函数，符合似然函数分布的这组数据的方差就是克拉美罗界。

一个特殊的例子：如果分布均为高斯分布，对数似然函数求二阶导再取倒数，即可得到克拉美罗界。

克拉美罗界的值不依赖于具体的信道估计方式，可以用来衡量信道估计方式的好坏的标准，即估计量的方差越靠近克拉美罗界，效果越好。

9.2 基于低分辨率的模数转换器

射频链的功率消耗和硬件成本随着模数转换器的位分辨率呈指数级增长。大规模MIMO需要采用低分辨率的模数转换器，低分辨率的模数转换器会导致接收信号失真，加大信道估计和数据检测难度。

1位ADCs只有一个比较器，没有自动增益控制，只有接收或发射数据的符号保留了下来，且丢失振幅信息。

举两个论文例子：

[MSW18]利用角度时域的稀疏性，首先将CSI矩阵估计转变为压缩感知问题，然后提出近似消息传递算法，该方法1位ADCs在低信噪比下逼近无限位ADCs性能，4位ADCs在中信噪比下逼近无限位ADCs性能。

[XQG+21]将上行信道估计问题建模为一个一位压缩感知问题，提出一个高效的无网格广义近似消息传递算法，可进行连续DOA估计。同时还可利用穷举搜索的近端梯度下降法用于下行链路信道估计。

[MSW18] J. Mo, P. Schniter, and R. W. Heath. Channel estimation in broadband millimeter wave MIMO systems with few-bit ADCs [J]. IEEE Transactions on Signal Processing, 2018, 66(5): 1141–1154.

[XQG+21] L. Xu, C. Qian, F. Gao, W. Zhang, and S. Ma. Angular domain channel estimation for mmWave massive MIMO with one-bit ADCs/DACs [J]. IEEE Transactions on Wireless Communications, 2021, 20(2): 969–982.

十. 基于透镜天线阵列的MIMO信道估计

初中物理告诉我们，凸透镜可以改变电磁波的传播方向。

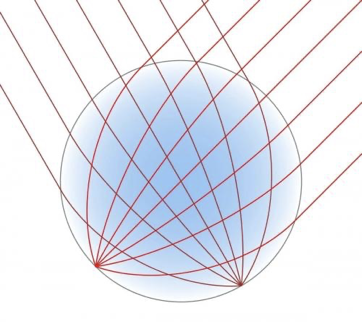
因为龙伯透镜可以让任何方向入射的电磁波，都会汇聚到球面上的某一个点上。目前国内研究比较好的有：紫金山实验室，中国移动。

透镜天线阵列的作用类似于离散傅里叶矩阵，能够将传输不同位置终端的信号集中在少量不同的发射天线上，形成波束空间信道。可以使得射频链个数大幅度减少，但给MIMO信道估计带来巨大挑战。

举一个论文的例子：[GDH17]提出一种低导频开销的基于非零值索引检测的信道估计，首先根据毫米波波束空间信道的稀疏性检测出信道非零值位置，然后利用LS算法进行求解（计算复杂度较高）。

[GDH17] X. Gao, L. Dai, S. Han, I. Chih-Lin, and X. Wang. Reliable beamspace channel estimation for millimeter-wave massive MIMO systems with lens antenna array [J]. IEEE Transactions on Wireless Communications, 2017, 16(9): 6010–6021.

十一. 基于神经网络的MIMO信道估计

深度学习在预测问题中具有良好的性能和较低复杂度。

• 利用深度学习直接学习从可用的信道相关信息到 CSI 的映射，来提高 CSI 估计性能或降低复杂度；

• “深度展开”技术，该技术对各种迭代优化算法进行展开，通过插入可学习参数提高信道估计性能；

总结

（1）细节总结

（2）合法端优化MIMO信道估计的方向

优化提高传统的最小二乘和最小均方误差MIMO信道估计：（1）不断迭代更新使用（2）仅使用LS获取初始信道估计信息，然后使用其他优化算法获取当前信道信息；
基于压缩感知的MIMO信道估计：（1）方法：最常用信道角域的块结构稀疏性（2）问题：需要将到达角和出发角离散到网格中，会出现网格不匹配问题；
基于解决“2”中问题的MIMO信道估计：（1）分布式压缩感知，可自适应匹配网格（2）结合原子范数去噪算法，精度更高，运算速度减慢；
基于用户快速移动的MIMO信道估计：（1）降低对信道稀疏性的要求（2）利用先验信息，直接估计下一状态信道信息【本质还是贝叶斯】（3）提取不同用户间共享的部分联合稀疏性；
MIMO硬件设施会减少射频链，信道估计则只能通过几个射频链路来获得压缩的信道表示，信道估计变得更难，如何解决：综合利用子阵列之间的公共稀疏性和子阵列内部的块稀疏结构；
MIMO会采用低分辨率的模数转换器，降低功率消耗。但会导致信号失真，信道估计变得更难，如何解决：近似消息传递算法，可将1位模数转换器的性能逼近无限位模数转化器；
基于神经网络的MIMO信道估计：（1）直接学习，直到可以从已有的信道信息映射到当前信道信息（2）对各种迭代算法进行展开，插入深度学习得到的参数，提高传统信道估计精度；