Spatial-Temporal Graph ODE Networks for Traffic Flow Forecasting
摘要
交通流量的复杂性和长范围时空相关性是难点
经典现存的工作:
1.利用浅图神经网络(shallow graph convolution networks)和 时间提取模块去分别建模空间和时间依赖
2.STGCN,DCRNN通过结合GNN和RNN,分别获得空间表示和时间表示
缺点:
-
浅图卷积神经网络不能获取长范围空间相关性(太浅特征学习不全面),仅仅考虑了空间上的连接,并没 有考虑语义连接(时间和空间上的关联)
2.分别考虑空间,时间——》模型效果不佳
-
GNN连接两层时效果最好,过深会导致过平滑问题,太浅导致特征学习不全,获取长范围依赖较难。
提出STGODE模型
1.基于张量的ODE模型 --》可以构建更深的网络,有效利用时空特征
2.添加语义邻接矩阵(更全面的获取特征)和时间空洞卷积(TCN 扩大卷积核,增大感受野)–》获取长时间依赖
STGODE组件
使用几个相关组件,解决现存问题
1.构建两种邻接矩阵spatial adjacency matrix (空间邻接矩阵)and semantic adjacency matrix(语义邻接矩阵),可以实现空间特征,语义相似的获取,准确描述时空相关性。
2.残差连接解决过平滑,残差连接的离散层被看作ODE的离散化。
带有残差连接的GNN——》避免过平滑,加深网络深度——》获得更广泛的时空依赖
利用时空张量——》同时考虑了时空交互,模型表现能力更好
使用空洞卷积——》感受野增大——》提取大范围特征
介绍
1.Traffic flow forecasting attempts to predict the future traffic flow given historical traffic conditions and underlying road networks
通过历史数据来预测未来数据
2.the complex and long-range spatial-temporal dependencies in traffic networks.
3.GNN可以高效处理图结构数据,通过聚合邻接点来更新节点表示
4.本文贡献:张量形式的GNN连续表示,加深网路,改善获取长范围时空相关
利用道路节点的空间邻域和语义邻域来综合考虑时空相关性
相关工作
GNN
1.GNN有效的邻接聚合方案
2.解决了非欧几里德图结构数据
缺点:为了获得长时空相关性——》加深网络——》造成过平滑
利用重启分布缓解过平滑为本文动机 (restart distribution)
残差结构可以被看做是离散的常微分方程,现在已经存在通过ODE将残差连接的GCN表达为连续的GCN工作。作者考虑将CGNN(continous graph neural network)应用于交通预测以处理GCN过平滑的问题并同时提取时空依赖
GCN为一种简单的ODE离散化,表示节点表示的连续动态,实现更深的网络。
参数定义
N个节点,A为邻接矩阵,大小为N*N
空间邻接矩阵为 Asp 语义邻接矩阵 Ase
图信号张量X,xit大小为1*F,节点i在t时刻的观测值,F作为一个观测向量的长度
Xt=(X1t,X2t,…XNt)大小为N*F,在t时刻所有点的交通情况
X=(X1,X2,…XT)大小为T*N *F,所有节点在所有时刻的交通量
正则化邻接矩阵

转换之后,可以进行特征值分解,值在【0,阿尔法】
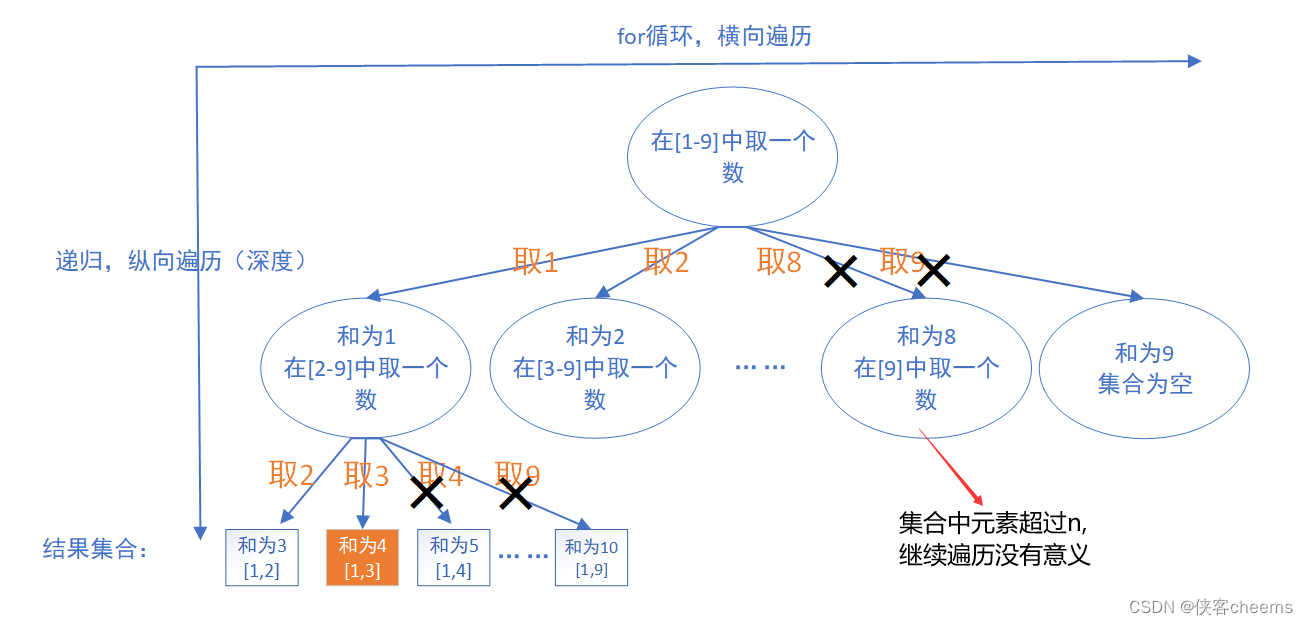
通过ODESolver实现神经网络参数化
模型
网络构成:两个ODE层(由多个STGODE block组成),一个最大值池化层,一个输出层
STGODE block 由 TCN(时间空洞卷积)+ ODESolver + TCN
TCN由空洞卷积和残差连接组成
ODESolver隐藏状态由当前状态和初始状态
邻接矩阵

去除一些关系较远的点,简化计算
语义相关矩阵
DTW算法——》计算两个时间序列的相似性(相较于逐点相似性,对形状相似性更加敏感)
DTW(X,Y)=D(m,n)为X和Y的最终距离


基于张量的时空图ODE

A 正则化矩阵
U时间变换矩阵
W特征转变矩阵
H0 GNN的初始输入

离散的格式如上图所示,其参数过多计算量过大。
ODESolver 可以实现时空融合,扩展网络深度,简化计算。
时间卷积模块

利用了空洞卷积,对每一个特征进行提取,然后再利用残差网络增强卷积性能
STGODE层
TCN+STGODESolver+TCN
优势:对时空信息敏感,卷积结构速度更快,并行性更好(空间邻接,语义邻接并行计算)
三明治法堆叠,扩展了获取复杂时空关系的能力
STGODE模块+最大值池化+两个MLP+Huber损失(对异常值的敏感性低于平方误差损失)
贡献:
我们利用基于张量的ODE框架来提取长距离时空相关性;
引入语义邻居来建立局部和全面的空间关系;
具有残差连接的时间扩张卷积网络有助于捕获长期时间相关性