1648. 销售价值减少的颜色球
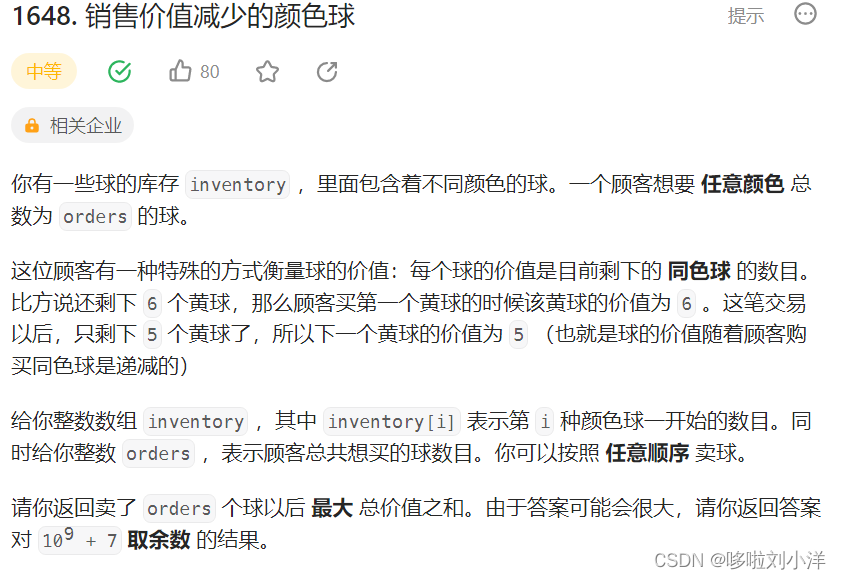

这道题不知为何总想记录下来,思路很简单,但是实现总是出错,这也许就是要记录的原因。再一个觉得题解写的比较难以理解,所以再细致一些解析。希望可以帮到实在搞不懂的同学
思路:
目的:我们需要取出orders个球,保证取出球的价值最大。
球的价值与它的个数成正比,第n个球的价值就是这个球目前的数量。
比如:a球有5个,此时取出一个a球,这个a球的价值是5,剩下4个a球。如果再取出一个a球,那么这个取出的a球的价值是4,以此类推。
那么很容易想到,每次取出数量最多的球不就好了?因为每次取出数量最多的球,也就是每次取出价值最大的球,每次取出最大价值的球,那么取n次,一定保证最终的价值最大。
提供三种思路,一次比一次好。
1.暴力排序
由于没次只需要拿到最多数量的球,那么可以考虑使用一个优先队列来存储球的数量,首先将球都放入队列,放入的过程自动排序。然后每次取队首元素即可。
class Solution
{
private:
int mod=1e9+7;
public:
int maxProfit(vector<int>& inventory, int orders)
{
//贪心,每次都拿最多的。用一个优先队列来维护
//准备工作,一个优先队列
priority_queue<int,vector<int>,less<int>>q;//less表示大堆,大的元素在队首,二叉树由顶至底元素越来越小
for(int i=0;i<inventory.size();i++) //加入元素
q.push(inventory[i]);
long long res=0;
for(int i=0;i<orders;i++)
{
int k=q.top(); //取队首元素
q.pop(); //弹出队首元素
q.push(k-1); //入队,由于队首元素取了一个,所以价值变小1,然后将其入队,入队过程会自动和其他队列元素排序,使得队列仍然满足从大到小的顺序排列
res=(res+k)%mod; //累加价值
}
return res;
return 0;
}
};
总结:不断排序的过程使时间复杂度超过限制。该方法思路没有问题,但是这个题目的测试数据不允许使用这种方法。
2.双指针
- 先将数组从大到小排序
- 准备两个指针left,right
那么left指针指向数组第一个元素(也是数组目前最大的元素),并且从此不会移动。
指针right指向数组第二大的元素。
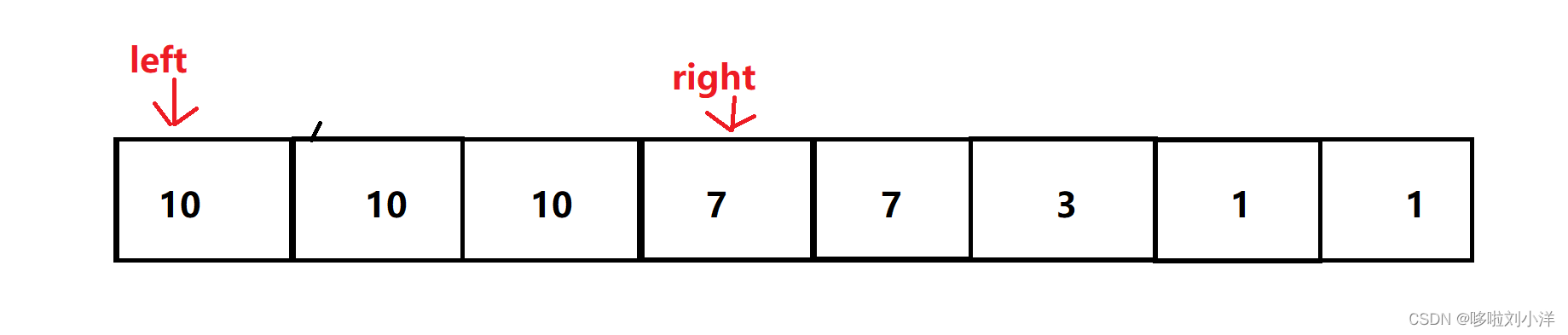
我们假设需要拿orders=15个球。 总价值用res记录
此时有两种选择
- [left,right)区间所有的球全拿
- [left,right)区间只取一部分
很明显,此时,最优选择是拿[left,right)区间的所有小球
r
e
s
+
=
(
10
+
9
+
8
)
∗
3
\ res+=(10+9+8)* 3
res+=(10+9+8)∗3
此时还剩下小球
o
r
d
e
r
s
=
15
−
9
=
6
\ orders=15-9=6
orders=15−9=6
那么此时数组变成这样

此时仍然有两种选择:
- [left,right)区间所有的球全拿
- [left,right)区间只取一部分
很显然,只需要取一部分即可。那么取哪一部分呢?
答案是:[left,right)的数从左到右轮流-1,一直循环如此直到取完小球。这样可以保证取得的价值最大。
看下面过程:
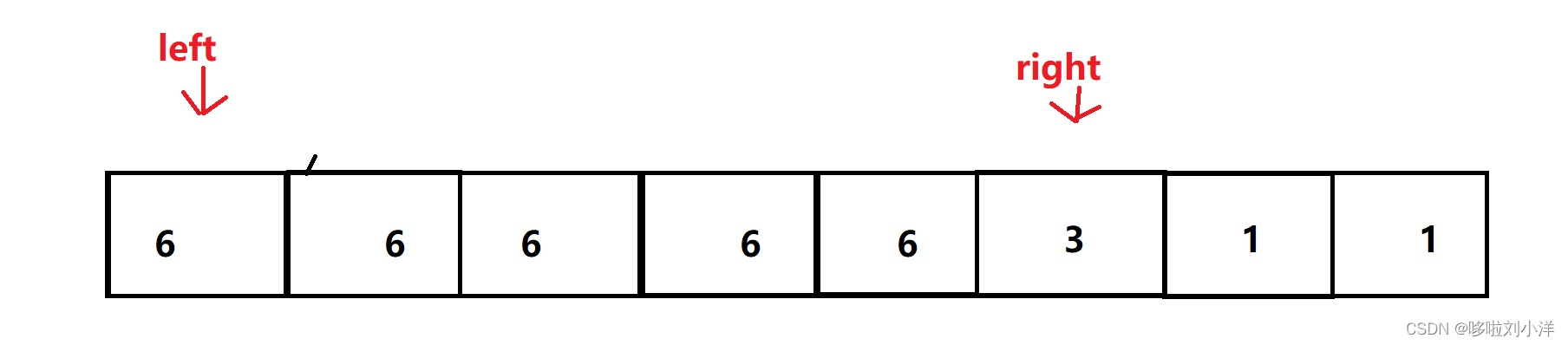
r
e
s
+
=
7
∗
5
\ res+=7*5
res+=7∗5
o
r
d
e
r
s
=
6
−
5
=
1
\ orders=6-5=1
orders=6−5=1
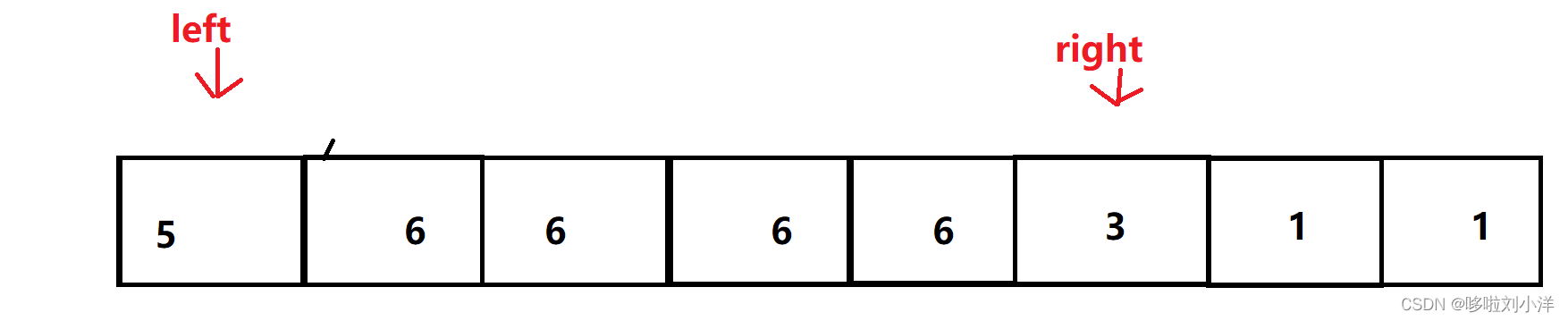
此时只需要取第一个小球就全部取完了
r
e
s
+
=
6
\ res+=6
res+=6
o
r
d
e
r
s
=
1
−
1
=
0
\ orders=1-1=0
orders=1−1=0
对于任意的小球数,都可以使用上面的步骤来。那么现在就是将这些步骤翻译成c的代码即可。
class Solution
{
private:
const int mod=1e9+7;
public:
static bool cmp(int a,int b) //定义比较规则,从大到小排序(a是左边的数,b是右边的数,左边的数大于右边的)
{
return a>b;
}
int maxProfit(vector<int>& inventory, int orders)
{
sort(inventory.begin(),inventory.end(),cmp); //从大到小排序
inventory.push_back(0); //加一个0在数组末尾,保证inventory[left]一定会大于inventory[right]
long long res=0; //统计答案
int n=inventory.size(); //数组元素个数
int left=0,right=0; //left始终指向第一个元素(最大的元素),right始终指向第二大的元素,那么[left,right)里面所有的元素都一样大
while(orders) //当小球还没有被取完
{
while(right<n&&inventory[left]==inventory[right])right++; //保证left,right分别指向第一大和第二大元素
//这时有两个选择,要么把[left,right)区间所有的球都取了(取到和inventory[right]一样多的数量)
//只取一部分,也就是说,[left,right)区间的球已经够了,不需要继续进行下一次while循环
//判断一下应该如何决策
if((long long int)(inventory[left]-inventory[right])*(right-left)<=orders) //如果取全部小于等于剩下需要的球,则取区间的全部(取到和inventory[right]数量一样)
{
long long int sum=(long long int)(inventory[left]+inventory[right]+1)*(inventory[left]-inventory[right])/2%mod; //1个数变成inventory[right]的价值。 等差数列求和公式sum=n*(a1+an)/2;
sum=sum*(right-left)%mod; //区间所有的数要加起来
res=(res+sum)%mod; //将此区间获得的价值累加
orders-=(inventory[left]-inventory[right])*(right-left);
inventory[left]=inventory[right]; //最大值改变,为什么不需要改变后面的值,不需要该,相当于前缀和一样,只需要对第一个数操作就等价于对后面的数操作
}
else //第二种选择,只取一部分(left,right区间的球满足最后的需求)
{
//先对[left,right)区间的所有数-1,看看可以减多少轮
int cnt=orders/(right-left);
long long sum=(long long int)cnt*(inventory[left]+inventory[left]-cnt+1)/2%mod; //inventory[left]变成inventory[left]-cnt+1的价值
sum=sum*(right-left)%mod; //区间[left,right)所有的数都有加上
res=(res+sum)%mod;
inventory[left]-=cnt; //最大值要改变
//r表示最后一轮应该从左到右取几个球
int r=orders-cnt*(right-left);
sum=(long long int )r*inventory[left]%mod;
res=(res+sum)%mod;
orders=0;
}
}
return res%mod;
}
};
此种方法虽然可以通过,但是效率很低
说句笑话,这个题就这个击败6.11%的我提交了58次才成功。花费了3到4个小时找问题

这说明代码能力和思维还是太菜了,需要继续坚持!!
3.二分
先说大概思路:
我们从结果出发,最后的数组只有两种情况:
- 全是0
- 不全是0
如果是第二种情况,那么将最后的数组排序,可以得到一个最大值集合,即所有最大值在一起的集合。
再来看没有取球的初始数组,也可以得到一个最大值集合,即所有最大数在一起的集合
我们知道,每次取球,都是从最大值集合里面取球,直到最大值集合所有的数都变成次大值,即次大值集合变成新的最大值集合。而且次大值集合的元素个数增加(之前的所有最大值集合的元素全部加到次大值集合当中)以此类推…
跳跃思维,一定有一个最大值Max,这个Max是取完球后剩下的元素里面的最大值。
我们把Max拿到初始数组(没有动过的数组inventory),那么由于最终数组不能有大于Max的元素,所以就很明了了
- 将所有大于Max的元素缩小到Max
- 所有小于等于Max的元素可以减小,也可以不变
只要Max能保证做完上述两个步骤后满足orders为0,则Max一定是合法的.
注意:
由于小于等于Max的元素既可以不变,也可以减小。那么说明一个Max可以对应多个orders.
但是要保证价值最大,所以能不去减小的,尽量不去减小,那么二分的时候就需要注意:
- 当Max取得的球>orders,那么Max一定不合法,因为此时Max连小于等于Max的数都还没有取球。然而还多了,所以一定不合法
- 当Max取得的球<orders,那么Max一定合法,因为可以减少后面小于Max的数添加球的个数一定可以达到orders。但是此时的Max不一定是价值最大。所以要继续缩小Max,Max越小,最后的总价值越大
一定要理解Max的含义和原理。
那么Max如何寻找?
二分初始数组的最大值。原因是因为最终数组的最大值一定小于等于初始数组的最大值.
- 如果当前的Max<=orders,说明球数量满足条件,但是价值不一定是最大,Max继续缩小,右边界左移
- 如果Max>orders,说明球过多,所以左边界右移
class Solution
{
private:
const int mod=1e9+7;
using LL=long long int;
public:
LL getValue(int a,int Max) //a是首项,Max是末项
{
//等差数列求和
return (LL)(a+Max)*(a-Max+1)/2%mod;
}
int maxProfit(vector<int>& inventory, int orders)
{
int left=0;
int right=*max_element(inventory.begin(),inventory.end());
int Max=-1;
while(left<=right)
{
int mid=(left+right)>>1;
LL total=accumulate(inventory.begin(),inventory.end(),0LL,[&](LL acc,int a){
return acc+max(a-mid,0);
}) ; //计算只减少大于mid的球的个数和,不统计小于mid的球
if(total<=orders) //满足条件,但是价值不一定最大,尝试减小mid
{
Max=mid;
right=mid-1;
}
else //不满足条件
{
left=mid+1;
}
}
//到这里,唯一的Max已经确定
//需要两步操作:(1)将大于Max的值减少到Max同时累计价值。 (2)如果将这些数都减去Max还不够orders个球,继续减少当前
//等于Max的球,一次减1个。
int rr=orders-accumulate(inventory.begin(),inventory.end(),0,[&](int acc,int a){ //有r个等于Max的值需要-1
//且r一定小于值为Max的元素数量,因为如果r大于等于MAx数量,那么Max就不是最优解
return acc+max(a-Max,0);
});
LL ans=0;
for(int a:inventory)
{
if(a>=Max)
{
if(rr>0)
{
rr--;
ans+=getValue(a,Max);
}
else
ans+=getValue(a,Max+1);
}
}
return ans%mod;
}
};
效率大大提高😋
好了,也算了却一个小心结,有需要帮助(虽然我很菜)的同学可以私信,会无不言😋






![[2.2.4]进程管理——FCFS、SJF、HRRN调度算法](https://img-blog.csdnimg.cn/img_convert/684703e6021f0d6c7a3061ef86b61097.png)