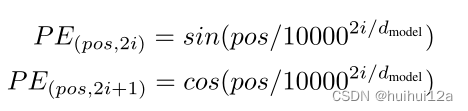**题目：**已知一个连续时间信号

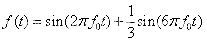
其中：f0=1HZ，取最高有限带宽频率fm=5f0。分别显示原连续时间信号波形和

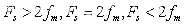
3种情况下抽样信号的波形。并画出它们的幅频特性曲线，并对采样后的信号进行恢复。

step1.绘制出采样信号
这部分相对简单，代码解释直接写在下面程序里。主要来说，通过for循环进行采样，采样后，根据采样频率间隔绘制出采样之后的离散信号。
代码1

%根据题目写出已知信息
f0=1;
fm=5*f0;
f=sin(2*pi*f0*t)+(1/3)*sin(6*pi*f0*t);
%设置时间区间和步进
t=-2:0.01:2;
%绘制出原始，未经采样的图像
subplot(411);
plot(t,f);
title('原始信号')

%for循环绘制不同采样频率下的信号
for i=1:1:3;
    fs=i*fm;
    Ts=1/fs;
    %Ts是采样周期，也是采样间隔
    n=-2:Ts:2;
    %写出采样后的离散信号
    f1=sin(2*pi*f0*n)+(1/3)*sin(6*pi*f0*n);
    %绘制剩下三个采样图像
    subplot(4,1,1+i);
    %以实心圆进行绘制
    stem(n,f1,'filled');
    

end

运行结果1

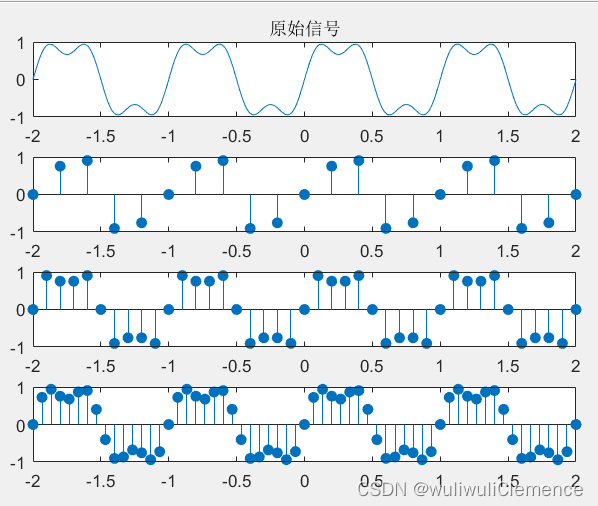
step2：绘制幅频特性曲线
这里主要使用的方法是傅里叶变换。根据傅里叶变换的公式，确定相关的变量。
代码2

%写出已知信息
f0=1;
fm=5*f0;
fs1=2*fm;
t=-2:0.01:2;
x=sin(2*pi*f0*t)+(1/3)*sin(6*pi*f0*t);

%对原始信号进行傅里叶变换
N=length(t);
k=0:N-1;%序号
wm=2*pi*fm;
w1=k*wm/N; %频域对应的角频率，wm/N可以理解为频率间隔，kwm/N，第k个点对应的频率
dt=1/fm %时域时间间隔
X=x*exp(-j*t'*w1)*dt%矩阵形式计算傅里叶变换
subplot(4,1,1);
plot(w1/(2*pi),abs(X));
axis([0,max(3*fm),1.1*min(abs(X)),1.1*max(abs(X))]);

%绘制fm,2fm,3fm采样频率下的频谱，对离散信号进行傅里叶变换
%写出离散信号后，进行傅里叶变换
for i=1:3; 
fs=i*fm;
 fs=i*fm;Ts=1/fs;
    n=-2:Ts:2;
    xs=sin(2*pi*f0*n)+1/3*sin(6*pi*f0*n);
    N=length(n);
    ws=2*pi*fs;
    k=0:N-1;
    n1=0:N-1;
    WN=exp(-2*pi*j/N);
    XS=xs*WN.^(n1'*k);
    
    w=k*ws/N;
    Xs=xs*exp(-j*n'*w)*Ts;
    %绘制关于频率变化的幅度谱（FT),绘制关于采样点的幅值和相角用DFT
    subplot(4,1,1+i);plot(w/(2*pi),abs(Xs));
    axis([0,max(4*fm),1.1*min(abs(Xs)),1.1*max(abs(Xs))]);
end

运行结果

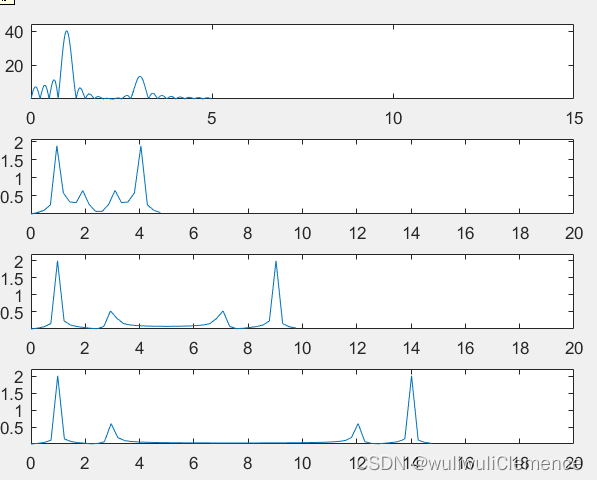
step3.抽样信号的恢复
这里信号的恢复，主要采用的方式是插值法。时域卷积是用时域抽样信号xs(t)与理想滤波器系统的单位冲激响应h(t)进行卷积积分来求解。卷积积分的公式通过推导化简为内插公式 。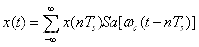
特别要注意生成$t-nTs$的这个过程，要很好的利用矩阵的规律。
目的：我们最后得到的应该是一个$1行(3\ast T0)/Ts列$的行向量。而抽样后的序列xs也是一个$1行(3\ast T0)/Ts列$的行向量，那么就要求$sa$是$(3\ast T0)/T行乘以(3\ast T0)/Ts列$的矩阵。而且$sa$取决于$t-nTs$
故借助该行代码生成$t-nTs$

  TN=ones(length(n),1)*t1-n'*Ts*ones(1,length(t1));

完整代码

%x信号重建
%写出已知条件
f0=1;
T0=1/f0;
fm=5*f0;
Tm=1/fm;%时域时间间隔
t=0:0.1:3*T0;
x=sin(2*pi*f0*t)+(1/3)*sin(6*pi*f0*t);
subplot(411);
plot(t,x);


%生成采样后的信号
for i=1:1:3
    fs=i*fm;
    Ts=1/fs;
    t1=0:Ts:3*T0;
    xs=sin(2*pi*f0*t1)+(1/3)*sin(6*pi*f0*t1);
    %生成t-nTs矩阵用于构建插值函数
    n=0:(3*T0)/Ts;
    TN=ones(length(n),1)*t1-n'*Ts*ones(1,length(t1));
    x1=xs*sinc(2*pi*fs*TN);
    
    subplot(4,1,1+i);
    plot(t1,x1);
     axis([min(t1),max(t1),1.1*min(x1),1.1*max(x1)])
end

运行结果

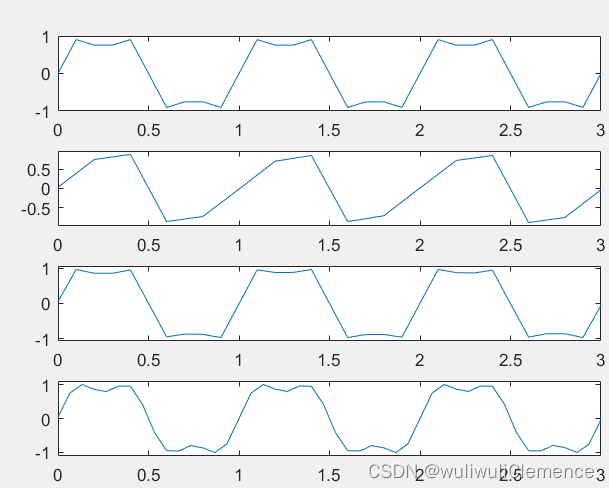
结果分析
由此次实验可以发现，当采样频率大于信号频率的两倍时，才可以进行恢复，也就是进行无失真传输。
经验
学习MATLAB往往先要想的是，我要达成的目的是什么，这个过程中，我需要用到的函数或者是公式是什么，为了实现这个函数的功能，我需要定义哪些变量。也就是说程序往往是先构建框架，再去填充内容。
此外，在这个过程中本人最怕的是矢量长度必须相等，索引超出矩阵维度。今天信号的恢复那里就卡了一下午，所以说，赤裸裸的教训，每一个变量都应该注意他的维度。