简介

去噪扩散概率模型(DDPM)在没有对抗性训练的情况下已经实现了高质量的图像生成，但它们需要模拟马尔可夫链许多步骤才能生成样本。

例如，从DDPM采样50k张大小为32 × 32的图像需要大约20个小时，而从Nvidia 2080 Ti GPU上的GAN采样则需要不到一分钟。这对于较大的图像来说就更成问题了，因为在相同的GPU上采样50k 256 × 256大小的图像可能需要近1000个小时。

为了加速采样，提出了去噪扩散隐式模型(DDIM)，这是一种更有效的迭代隐式概率模型，具有与ddpm相同的训练过程。

在DDPM中，生成过程被定义为特定马尔可夫扩散过程的反向。这些非马尔可夫过程可以对应于确定性的生成过程，从而产生隐式模型，从而更快地生成高质量的样本。

经验证明，与DDPM相比，DDIM可以以10倍到50倍的速度生成高质量的样本，允许权衡计算和样本质量，直接在潜在空间中执行语义上有意义的图像插值，并以非常低的误差重建观测。

非马尔可夫正向过程的变分推理

因为生成式模型近似于推理过程的反向，需要重新思考推理过程，以减少生成式模型所需的迭代次数

关键想法是 DDPM 目标函数 $L_y$ 仅仅依赖于边缘分布 $q(x_t|x_0)$ ,而不是直接依赖于联合发布 $q(x_{1:T} | x_0)$
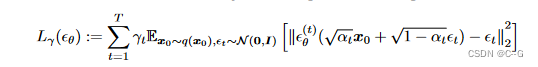
在这里插入图片描述

在这里插入图片描述

也就是说在推导出目标函数 $L_{y}$ 的过程中，没有用到 $q(x_{1:T}|x_0)$ 的具体形式，只是基于贝叶斯公式和 $q(x_t|x_{t-1},x_0)、q(x_t|x_0)$ 表达式

在训练DDPM所用到的 $L_y$ loss中，甚至没有采用和 $q(x_t|x_{t-1},x_0)$ 相关的系数，而是直接选择将预测噪声的权重设置为 1。

由于噪声项是来自 $q(x_t|x_0)$ 的采样，因此，DDPM的目标函数其实只由 $q(x_t|x_0)$ 表达式决定。

所以，只要 $q(x_t | x_0)$ 已知并且是高斯分布的形式，那么就可以用DDPM的预测噪声的目标函数 $L_{y}$ 来训练模型

在DDPM中，基于马尔可夫性质 $q(x-t | x_{t-1},x_0) = q(x_t | x_{t-1})$

那么如果是服从非马尔科性质， $q(x-t | x_{t-1},x_0)$ 应该具有更一般的形式，以及只要保证 q(x_t | x_0) 的形式不变，那么就可以直接复用训好的DDOM，只不过使用新的概率分布来进行逆过程的采样

论文探索了非马尔可夫的替代推断过程，如下图右新的生成过程
在这里插入图片描述

非马尔科夫的前向扩散过程

Let us consider a family Q of inference distributions, indexed by a real vector $R^T_{≥0}$ :
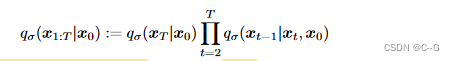
在这里插入图片描述
对于所有 t > 1，都满足 $q_\sigma(x_T|x_0) = N(\sqrt{\alpha_{t-1}}x_0 + (1-\alpha_T)I)$

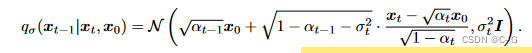
由上述三公式，可以推出对任意时刻 t 都满足 $q_\sigma(x_t|x_0) = N(\sqrt{\alpha_t}x_0,(1-\alpha_t)I)$

前向过程可以从贝叶斯定理推导出来
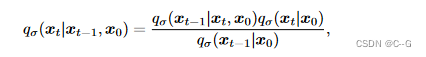
在这里插入图片描述
仍然是服从高斯分布的，但是前向过程不再是马尔科夫链，因为 $x_t$ 可以同时依赖于 $x_{t-1},x_0$

σ 的大小决定前向过程的随机程度，当 $\sigma \rightarrow 0$ 达到了一个极端的情况，只要对某个t 观察 $x_0$ 和 $x_t$ ，那么 $x_{t−1}$ 就成为已知和固定的。

数学补充

边缘分布与条件分布
在这里插入图片描述
数学归纳法

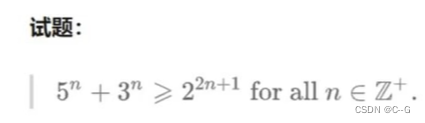
证明任意时刻 t 都满足 $q_\sigma(x_t|x_0) = N(\sqrt{\alpha_t}x_0,(1-\alpha_t)I)$

利用数学归纳法，假设 $\leq T$ 时刻满足 $q_\sigma(x_t|x_0) = N(\sqrt{\alpha_t}x_0,(1-\alpha_t)I)$ ，只要再证明同时满足 $q_\sigma(x_{t-1}|x_0) = N(\sqrt{\alpha_{t-1}}x_0,(1-\alpha_{t-1})I)$

这样就可以证明对于任意 t 从 T 到 1 都满足（t = T 时已满足）

由贝叶斯公式得
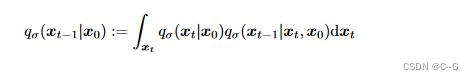
在这里插入图片描述
又因为

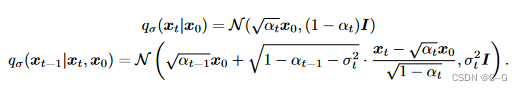
利用边缘分布与条件分布关系，得到

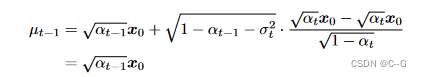
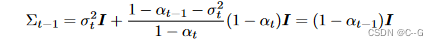
因此，得证

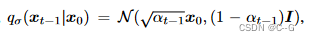
对比非马尔科夫扩散后验分布与DDPM马尔可夫扩散的后验分布

DDPM马尔可夫扩散的后验分布
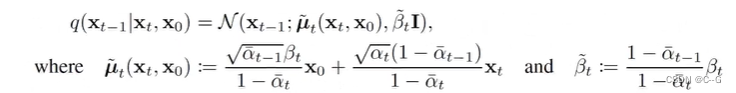
在这里插入图片描述
非马尔可夫扩散的后验分布

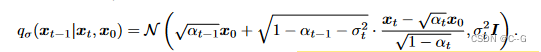
DDIM中 $\alpha$ 表示DDPM中 $\bar{\alpha}$

为了方便对比，将DDIM公式转换为统一符号如下：

$\begin{aligned} q_\sigma(x_{t-1}|x_t,x_0) &= N(\sqrt{\bar{\alpha}_{t-1}}x_0 + \sqrt{1-\bar{\alpha}_{t-1}-\sigma^2_t} \cdot \frac{x_t -\sqrt{\bar{\alpha}_t}x_0 }{\sqrt{1-\bar{\alpha}_t}},\sigma^2I) \end{aligned}$

非马尔科夫扩散反向过程采样

定义应该可训练的生成过程 $p_\theta(x_{0:T})$ 。利用 $q_\theta(x_{t-1}|x_t,x_0)$ 得到每个 $p^{(t)}_\theta(x_{t-1} | x_t)$

直观来说，给定一个有噪声的 $x_t$ ，首先预测一个 $x_0$ ，然后通过 $q_\theta(x_{t-1}|x_t,x_0)$ 进行采样

对于 $x_0 \sim q(x_0)，\epsilon_t \sim N(0,I)，x_t$ 可以从DDPM前向过程公式 $x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon，where \ \epsilon \sim N(0,I)$ 得到，反过来，可以利用模型预测的 $\epsilon_t$ 和 $x_t$ ，得到 $x_0$ ，这里定义为去噪的观测值：
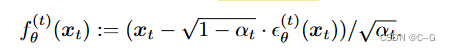
在这里插入图片描述
那么就可以通过一个固定的先验 $p_\theta(x_T) = N(0,I)$ 定义前向过程，反向过程采样如下公式

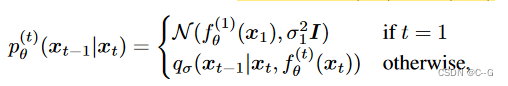
其中 $q_\theta(x_{t-1}|x_t,f^{(t)}_\theta(x_t))$ 为上面定义的反向采样过程， $x_0$ 使用 $f^{(t)}_\theta(x_t)$ 替换。

当 t = 1 时，这里用了一个高斯噪声 (方差为 $\sigma^2I$ )，保证前向过程处处支持

非马尔可夫扩散过程目标函数

DDIM的目标函数可以用于优化 DDPM目标函数，证明如下
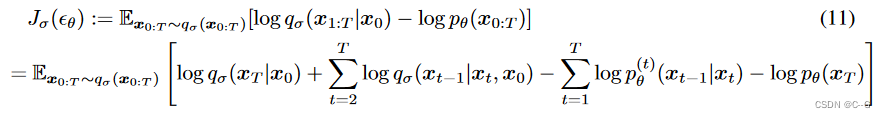
在这里插入图片描述
从 $J_σ$ 的定义来看，似乎每个 σ 的选择都需要训练不同的模型，因为它对应于不同的变分目标(以及不同的生成过程)。然而，对于某些权重的 γ ， $J_σ$ 等价于 $L_γ$ ，如下所示。

定理：对于 σ >0，存在 $γ∈R^T_{>0}$ 和 C∈R，使得 $J_σ = L_γ + C$ 。

变分目标 $L_γ$ 的特殊之处在于，如果模型 $\epsilon_\theta^{(t)}$ 的参数 θ 在不同的 t 上不共享，那么 $\epsilon_\theta$ 的最优解将不依赖于权重 γ (因为全局最优是通过分别最大化和中的每一项来实现的)。

$L_γ$ 的这种性质有两个含义。一方面，这证明了使用 $L_1$ 作为DDPM 变分下界的替代目标函数是合理的;另一方面，由于 $J_σ$ 等价于上述定理中的某个 $L_γ$ ，因此 $J_σ$ 的最优解也与 $L_1$ 的最优解相同。因此，如果在模型 $\epsilon_\theta$ 中参数不跨 t 共享，那么Ho等人(2020)使用的 $L_1$ 目标也可以用作变分目标 $J_σ$ 的替代目标。

证明：
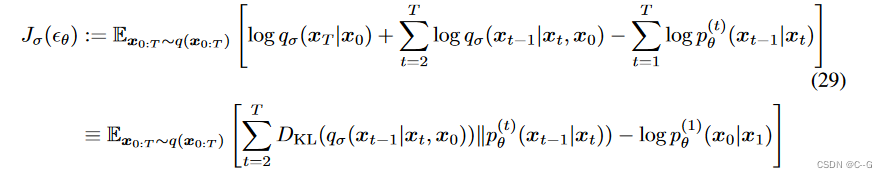
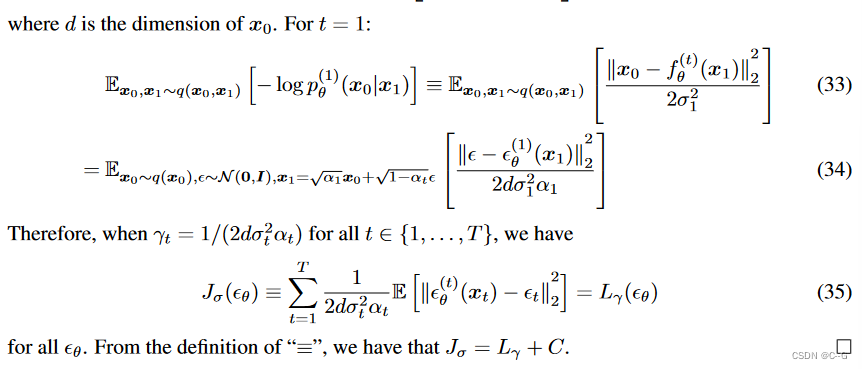
在这里插入图片描述

特殊的采样–DDIM（含蓄的概率扩散模型）

注意：DDPM中的 $\bar{\alpha}$ 在DDIM 论文中为 $\alpha$

DDIM 反向过程利用重参数技巧可以写成如下：
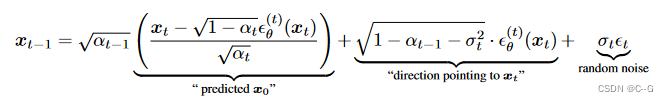
在这里插入图片描述
$\epsilon_t \sim N(0,I)$ 表示独立于 $x_t$ 的标准高斯噪声，定义 $\alpha_0 := 1$ 。

使用同一模型 $\epsilon_t$ 不同的 σ 值导致不同的前向生成过程，所以 re-training 模型是不必要的

对于所有 t，当 $\sigma_t = \sqrt{ \frac{ (1-\alpha_{t-1})} { (1-\alpha_t) } } \sqrt{ \frac{1-\alpha_t}{\alpha_{t-1}} }$ 时，相当于DDPM

当 $\sigma_t = 0$ ，这个过程就是确定性采样。
给定 $x_{t-1}$ 和 $x_0$ ，除了 t = 1,前向过程变成确定性过程。在前向过程中，随机噪声 $\epsilon_t$ 系数为 0，因此产生的模型成为了一个隐私概率模型，其中样本是用固定的过程（从 $x_T$ 到 $x_0$ ）从潜在变量生成的，这样前向过程不再是扩散过程了。命名为 DDIM

$L_1$ 的特殊性质带来一种加速采样技巧–respacing

由于去噪目标 $L_1$ 不依赖于特定的正向过程，只要 $q_σ(x_t|x_0)$ 是固定的，也可以考虑长度小于 T 的正向过程，这样可以加速相应的生成过程，而无需训练不同的模型。

正向过程不是在所有潜在变量 $x_{1:T}$ 上定义的，而是在一个子集{ $x_{τ_1}，……， x_{τ_S}$ }，其中 $τ$ 是 [1，…] 的递增子序列。特别地，定义了顺序前向过程 $x_{τ_1}，…， x_{τ_S}$ ，使 $q(x_{τ_i }|x_0) = N(\sqrt{α_{τ_i}}x_0，(1−α_{τ_i})I)$ 符合“边缘值”。生成过程现在根据反向( $τ$ )对潜在变量进行采样，称之为(采样)轨迹。当采样轨迹的长度远小于 T 时，由于采样过程的迭代性质，可以实现计算效率的显著提高。

也就是说，可以用任意数量的前向步骤训练模型，但在生成过程中只从其中的一些步骤中取样

实验

当考虑更少的迭代时，DDIM在图像生成方面优于DDPM，在原始DDPM生成过程中提供10倍到100倍的速度

与DDPM不同的是，一旦初始潜在变量 $x_T$ 固定，DDIM 将保留高级图像特征，而不管生成轨迹如何，因此它们能够直接从潜在空间执行插值

DDIM 还可以用于编码样本，从潜在代码中重建样本，由于随机采样过程，DDPM无法做到这一点。

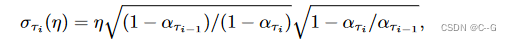
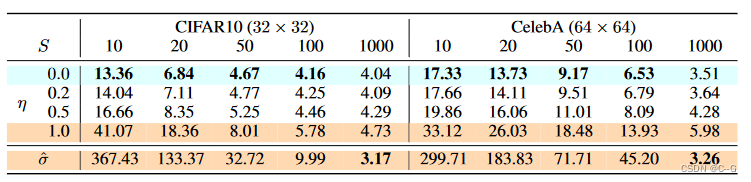
在这里插入图片描述
论文考虑不同的 $\sigma$ ，当 $\eta$ = 0 即为 DDIM，当 $\eta$ = 1 即为 DDPM，此外可以考虑 0 -1 间的 $\eta$ ，表示不同的噪声

还考虑了随机噪声的标准偏差大于σ(1)的DDPM，计为 $\hat{\sigma}: \hat{\sigma_{\tau_i}} = \sqrt{ \frac{1- \alpha_{\tau_i}}{\alpha_{\tau_{i-1}}} }$

在这里插入图片描述

代码

training_losses回顾

    def training_losses(self, model, x_start, t, model_kwargs=None, noise=None):
        """
        Compute training losses for a single timestep.

        :param model: the model to evaluate loss on.
        :param x_start: the [N x C x ...] tensor of inputs.
        :param t: a batch of timestep indices.
        :param model_kwargs: if not None, a dict of extra keyword arguments to
            pass to the model. This can be used for conditioning.
        :param noise: if specified, the specific Gaussian noise to try to remove.
        :return: a dict with the key "loss" containing a tensor of shape [N].
                 Some mean or variance settings may also have other keys.
        """
        if model_kwargs is None:
            model_kwargs = {}
        if noise is None:
            noise = th.randn_like(x_start)
        x_t = self.q_sample(x_start, t, noise=noise)

        terms = {}

        if self.loss_type == LossType.KL or self.loss_type == LossType.RESCALED_KL:
            terms["loss"] = self._vb_terms_bpd(
                model=model,
                x_start=x_start,
                x_t=x_t,
                t=t,
                clip_denoised=False,
                model_kwargs=model_kwargs,
            )["output"]
            if self.loss_type == LossType.RESCALED_KL:
                terms["loss"] *= self.num_timesteps
        elif self.loss_type == LossType.MSE or self.loss_type == LossType.RESCALED_MSE:
            model_output = model(x_t, self._scale_timesteps(t), **model_kwargs)

            if self.model_var_type in [
                ModelVarType.LEARNED,
                ModelVarType.LEARNED_RANGE,
            ]:
                B, C = x_t.shape[:2]
                assert model_output.shape == (B, C * 2, *x_t.shape[2:])
                model_output, model_var_values = th.split(model_output, C, dim=1)
                # Learn the variance using the variational bound, but don't let
                # it affect our mean prediction.
                frozen_out = th.cat([model_output.detach(), model_var_values], dim=1)
                terms["vb"] = self._vb_terms_bpd(
                    model=lambda *args, r=frozen_out: r,
                    x_start=x_start,
                    x_t=x_t,
                    t=t,
                    clip_denoised=False,
                )["output"]
                if self.loss_type == LossType.RESCALED_MSE:
                    # Divide by 1000 for equivalence with initial implementation.
                    # Without a factor of 1/1000, the VB term hurts the MSE term.
                    terms["vb"] *= self.num_timesteps / 1000.0

            target = {
                ModelMeanType.PREVIOUS_X: self.q_posterior_mean_variance(
                    x_start=x_start, x_t=x_t, t=t
                )[0],
                ModelMeanType.START_X: x_start,
                ModelMeanType.EPSILON: noise,
            }[self.model_mean_type]
            assert model_output.shape == target.shape == x_start.shape
            terms["mse"] = mean_flat((target - model_output) ** 2)
            if "vb" in terms:
                terms["loss"] = terms["mse"] + terms["vb"]
            else:
                terms["loss"] = terms["mse"]
        else:
            raise NotImplementedError(self.loss_type)

        return terms

采样 $x_{t-1}$

    def ddim_sample(
        self,
        model,
        x,
        t,
        clip_denoised=True,
        denoised_fn=None,
        model_kwargs=None,
        eta=0.0,
    ):
        """
        Sample x_{t-1} from the model using DDIM.

        Same usage as p_sample().
        """
        out = self.p_mean_variance(
            model,
            x,
            t,
            clip_denoised=clip_denoised,
            denoised_fn=denoised_fn,
            model_kwargs=model_kwargs,
        )
        # Usually our model outputs epsilon, but we re-derive it
        # in case we used x_start or x_prev prediction.
        eps = self._predict_eps_from_xstart(x, t, out["pred_xstart"])
        alpha_bar = _extract_into_tensor(self.alphas_cumprod, t, x.shape)
        alpha_bar_prev = _extract_into_tensor(self.alphas_cumprod_prev, t, x.shape)
        sigma = (
            eta
            * th.sqrt((1 - alpha_bar_prev) / (1 - alpha_bar))
            * th.sqrt(1 - alpha_bar / alpha_bar_prev)
        )
        # Equation 12.
        noise = th.randn_like(x)
        mean_pred = (
            out["pred_xstart"] * th.sqrt(alpha_bar_prev)
            + th.sqrt(1 - alpha_bar_prev - sigma ** 2) * eps
        )
        nonzero_mask = (
            (t != 0).float().view(-1, *([1] * (len(x.shape) - 1)))
        )  
        # no noise when t == 0
        sample = mean_pred + nonzero_mask * sigma * noise
        return {"sample": sample, "pred_xstart": out["pred_xstart"]}

反向过程循环采样

    def ddim_sample_loop_progressive(
        self,
        model,
        shape,
        noise=None,
        clip_denoised=True,
        denoised_fn=None,
        model_kwargs=None,
        device=None,
        progress=False,
        eta=0.0,
    ):
        """
        Use DDIM to sample from the model and yield intermediate samples from
        each timestep of DDIM.

        Same usage as p_sample_loop_progressive().
        """
        if device is None:
            device = next(model.parameters()).device
        assert isinstance(shape, (tuple, list))
        if noise is not None:
            img = noise
        else:
            img = th.randn(*shape, device=device)
        indices = list(range(self.num_timesteps))[::-1]

        if progress:
            # Lazy import so that we don't depend on tqdm.
            from tqdm.auto import tqdm

            indices = tqdm(indices)

        for i in indices:
            t = th.tensor([i] * shape[0], device=device)
            with th.no_grad():
                out = self.ddim_sample(
                    model,
                    img,
                    t,
                    clip_denoised=clip_denoised,
                    denoised_fn=denoised_fn,
                    model_kwargs=model_kwargs,
                    eta=eta,
                )
                yield out
                img = out["sample"]

反向过程生成样本

    def ddim_sample_loop(
        self,
        model,
        shape,
        noise=None,
        clip_denoised=True,
        denoised_fn=None,
        model_kwargs=None,
        device=None,
        progress=False,
        eta=0.0,
    ):
        """
        Generate samples from the model using DDIM.

        Same usage as p_sample_loop().
        """
        final = None
        for sample in self.ddim_sample_loop_progressive(
            model,
            shape,
            noise=noise,
            clip_denoised=clip_denoised,
            denoised_fn=denoised_fn,
            model_kwargs=model_kwargs,
            device=device,
            progress=progress,
            eta=eta,
        ):
            final = sample
        return final["sample"]

respace

按需生成子序列- t

def space_timesteps(num_timesteps, section_counts):
    """
    Create a list of timesteps to use from an original diffusion process,
    given the number of timesteps we want to take from equally-sized portions
    of the original process.

    For example, if there's 300 timesteps and the section counts are [10,15,20]
    then the first 100 timesteps are strided to be 10 timesteps, the second 100
    are strided to be 15 timesteps, and the final 100 are strided to be 20.

    If the stride is a string starting with "ddim", then the fixed striding
    from the DDIM paper is used, and only one section is allowed.

    :param num_timesteps: the number of diffusion steps in the original
                          process to divide up.
    :param section_counts: either a list of numbers, or a string containing
                           comma-separated numbers, indicating the step count
                           per section. As a special case, use "ddimN" where N
                           is a number of steps to use the striding from the
                           DDIM paper.
    :return: a set of diffusion steps from the original process to use.
    """
    if isinstance(section_counts, str):
        if section_counts.startswith("ddim"):
            desired_count = int(section_counts[len("ddim") :])
            for i in range(1, num_timesteps):
                if len(range(0, num_timesteps, i)) == desired_count:
                    return set(range(0, num_timesteps, i))
            raise ValueError(
                f"cannot create exactly {num_timesteps} steps with an integer stride"
            )
        section_counts = [int(x) for x in section_counts.split(",")]
    size_per = num_timesteps // len(section_counts)
    extra = num_timesteps % len(section_counts)
    start_idx = 0
    all_steps = []
    for i, section_count in enumerate(section_counts):
        size = size_per + (1 if i < extra else 0)
        if size < section_count:
            raise ValueError(
                f"cannot divide section of {size} steps into {section_count}"
            )
        if section_count <= 1:
            frac_stride = 1
        else:
            frac_stride = (size - 1) / (section_count - 1)
        cur_idx = 0.0
        taken_steps = []
        for _ in range(section_count):
            taken_steps.append(start_idx + round(cur_idx))
            cur_idx += frac_stride
        all_steps += taken_steps
        start_idx += size
    return set(all_steps)

重写扩散模型

class SpacedDiffusion(GaussianDiffusion):
    """
    A diffusion process which can skip steps in a base diffusion process.

    :param use_timesteps: a collection (sequence or set) of timesteps from the
                          original diffusion process to retain.
    :param kwargs: the kwargs to create the base diffusion process.
    """

    def __init__(self, use_timesteps, **kwargs):
        self.use_timesteps = set(use_timesteps)
        self.timestep_map = []
        self.original_num_steps = len(kwargs["betas"])

        base_diffusion = GaussianDiffusion(**kwargs)  # pylint: disable=missing-kwoa
        last_alpha_cumprod = 1.0
        new_betas = []
        for i, alpha_cumprod in enumerate(base_diffusion.alphas_cumprod):
            if i in self.use_timesteps:
                new_betas.append(1 - alpha_cumprod / last_alpha_cumprod)
                last_alpha_cumprod = alpha_cumprod
                self.timestep_map.append(i)
        kwargs["betas"] = np.array(new_betas)
        super().__init__(**kwargs)

    def p_mean_variance(
        self, model, *args, **kwargs
    ):  # pylint: disable=signature-differs
        return super().p_mean_variance(self._wrap_model(model), *args, **kwargs)

    def training_losses(
        self, model, *args, **kwargs
    ):  # pylint: disable=signature-differs
        return super().training_losses(self._wrap_model(model), *args, **kwargs)

    def _wrap_model(self, model):
        if isinstance(model, _WrappedModel):
            return model
        return _WrappedModel(
            model, self.timestep_map, self.rescale_timesteps, self.original_num_steps
        )

    def _scale_timesteps(self, t):
        # Scaling is done by the wrapped model.
        return t

t 步骤映射，模型包裹


class _WrappedModel:
    def __init__(self, model, timestep_map, rescale_timesteps, original_num_steps):
        self.model = model
        self.timestep_map = timestep_map
        self.rescale_timesteps = rescale_timesteps
        self.original_num_steps = original_num_steps

    def __call__(self, x, ts, **kwargs):
        map_tensor = th.tensor(self.timestep_map, device=ts.device, dtype=ts.dtype)
        new_ts = map_tensor[ts]
        if self.rescale_timesteps:
            new_ts = new_ts.float() * (1000.0 / self.original_num_steps)
        return self.model(x, new_ts, **kwargs)