一：背景介绍

问题描述

因为某些特殊原因需要把nacos迁移到另一个版本的nacos(我迁的是nacos2.0.2版本.)
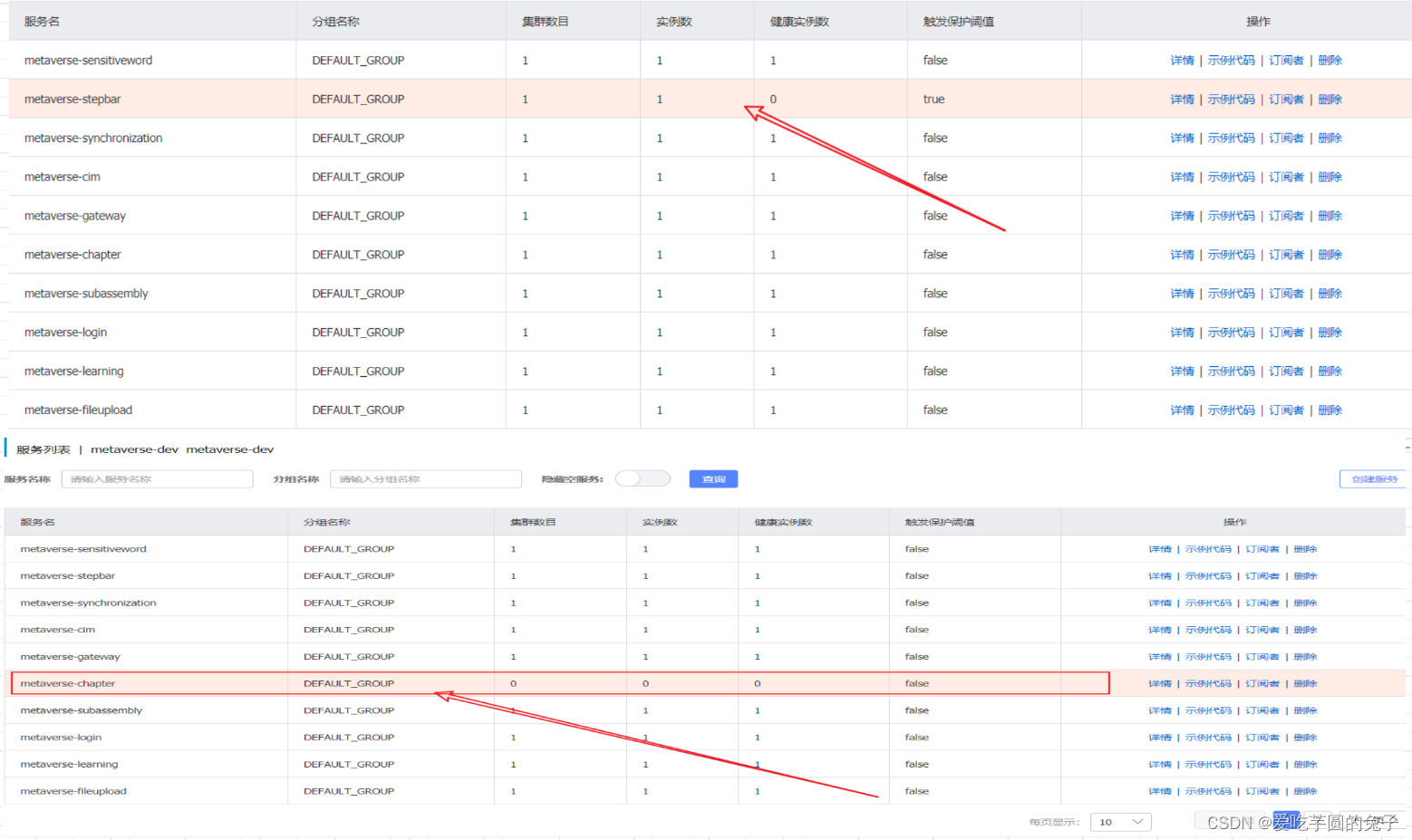
迁移完成后,Nacos注册中心有一个微服务有多台实例的时候，点击一个实例下线操作，报错

caused: errCode: 500, errMsg: do metadata operation failed ;caused:com.alibaba.nacos.consistency.exception.ConsistencyException:com.alibaba.nacos.core.distributed.raft.exception.NoLeaderException: The Raft Group [naming_instance_metadata] did not find the Leader node;caused:com.alibaba.nacos.core.distributed.raft.exception.NoLeaderException:The Raft Group [naming_instance_metadata] did not find the Leader node;

解决

注册的ip混乱，导致出现该问题，先停服务，再停nacos，再删掉data目录下的protocol文件夹，再重启nacos。最后在重启需要注册的那些服务

二：问题分析过程

解决过程设计到的知识

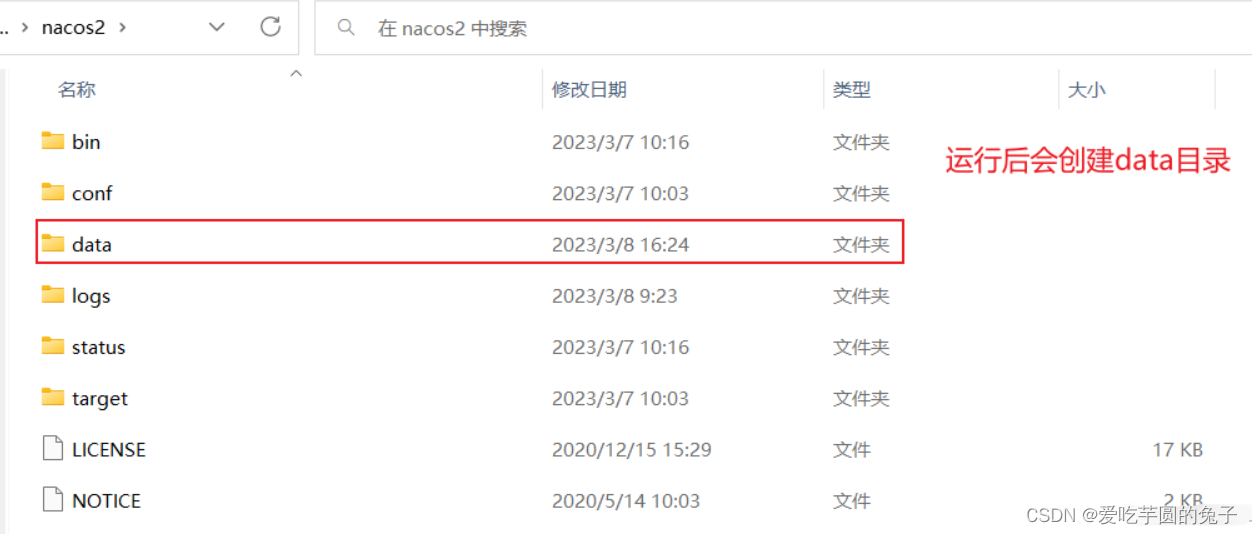
1、nacos的data目录作用。

nacos的data目录是用来存储nacos服务的数据的，包括配置信息，服务信息等。默认的情况下，data目录位于naocs安装目录下的。

2、nacos data目下的protocol目录

nacos的data目录下的protocol目录是用来存储。服务中心的协议信息的，它记录了服务注册中心所使用的协议类型，版本号等等。以便于服务提供者和服务消费者之间进行通信。

3、nacos ip混乱问题

nacos的ip混乱。可能是因为网络配置不正确，或者服务注册不规范导致的。可以通过检查网络配置和服务注册情况来解决这个问题。我们这里使用的解决问题是注册的服务全部删掉，然后重新注册解决的。

三：总结

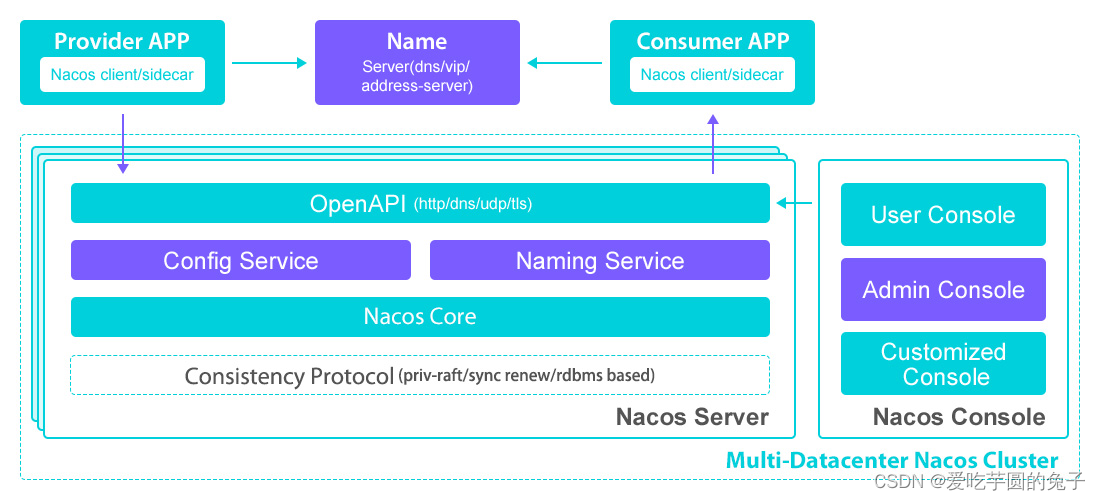
大家可以参考一下：link