什么是基数排序？

基数排序：基数排序（Radix sort）是一种非比较型整数排序算法， 基本思想主要是通过关键字间的比较和移动记录这两种操作，而实现基数排序不需要进行关键字间的比较，基数排序是一种借助于关键字的思想对单逻辑关键字进行排序的方法。

基本原理

基本原理：将整数按位数切割成不同的数字，然后按每个位数分别比较。基数排序的方式可以采用LSD（Least significant digital）或MSD（Most significant digital），LSD的排序方式由键值的最右边开始，而MSD则相反，由键值的最左边开始。
MSD(最高位优先)：先从高位开始进行排序，在每个关键字上，可采用计数排序。
LSD(最低位优先)：先从低位开始进行排序，在每个关键字上，可采用桶排。

核心思想

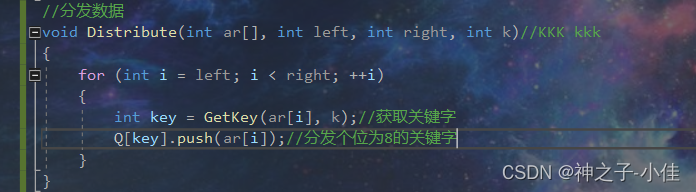
1.分发数据

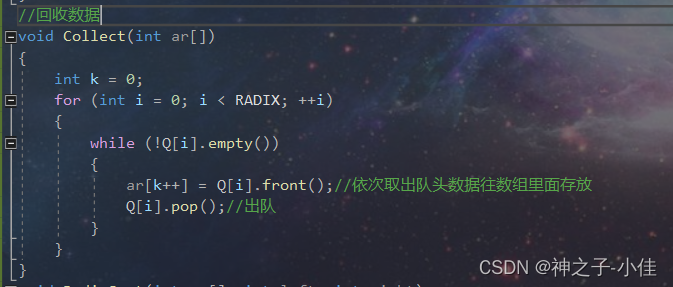
2.回收数据

实现逻辑

实现逻辑：
① 将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。
② 从最低位开始，依次进行一次排序。
③ 这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有

代码实现

#include<iostream>
#include<stdio.h>
#include<queue>
using namespace std;
#define K 3//位数是3
#define RADIX 10//基数是10个
//定义基数
queue<int> Q[RADIX];
int GetKey(int value, int k)由低到高获取位数key
{
	int key = 0;
	while (k >= 0)
	{
		key = value % 10;//8 7 2
		value /= 10;//278 27 2
		k--;
	}
	return key;
}
//分发数据
void Distribute(int ar[], int left, int right, int k)
{
	for (int i = left; i < right; ++i)
	{
		int key = GetKey(ar[i], k);//依次获取关键字
		Q[key].push(ar[i]);//依次分发个位为8 7 2的关键字
	}
}
//回收数据
void Collect(int ar[])
{
	int k = 0;
	for (int i = 0; i < RADIX; ++i)
	{
		while (!Q[i].empty())
		{
			ar[k++] = Q[i].front();//依次取出队头数据往数组里面存放
			Q[i].pop();//出队
		}
	}
}
void RadixSort(int ar[], int left, int right)//基数排序
{
	for (int i = 0; i < K; i++)//注意这个是我们定义的宏大写K
	{
		Distribute(ar, left, right, i);
		Collect(ar);
	}
}
void main()
{
	int ar[] = { 278,109,63,930,589,184,505,269,8,83 };
	int n = sizeof(ar) / sizeof(ar[0]);//n表示数组元素的个数
	for (int i = 0; i < n; i++)
	{
		printf("%d ", ar[i]);
	}
	printf("\n");
	printf("\n");
	//基数排序
	RadixSort(ar, 0, n);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", ar[i]);
	}
	printf("\n");
	system("pause");
}

运行结果：

复杂度分析

复杂度分析：
时间复杂度：O(k*N)
空间复杂度：O(k + N)
稳定性：稳定

总结

基数排序与计数排序、桶排序这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：
基数排序：根据键值的每位数字来分配桶；
计数排序：每个桶只存储单一键值；
桶排序：每个桶存储一定范围的数值；
基数排序不是直接根据元素整体的大小进行元素比较，而是将原始列表元素分成多个部分，对每一部分按一定的规则进行排序，进而形成最终的有序列表。