【数据结构】带你深入理解栈

news2024/12/26 2:20:18

一. 栈的基本概念💫

栈是一种特殊的线性表。其只允许在固定的一端进行插入和删除元素的操作，进行数据的插入和删除的一端称作栈顶，另外一端称作栈底。栈不支持随机访问，栈的数据元素遵循后进先出的原则，即LIFO（Late In First Out）。

也许有人曾经听说过压栈和入栈的术语，以下是它们的定义：

压栈：栈的插入操作叫做进栈/压栈/入栈，插入数据是在栈顶
出栈：栈的删除操作叫做出栈/弹栈，删除数据也是在栈顶

我们结合动图来理解栈的后进先出：

二. 栈实现方法的分析与选择👉

2.1 引入

我们可以使用顺序存储结构或者链式存储结构来实现栈。换句话来说，我们可以使用之前学习过的顺序表或者链表来实现栈，它们各自有自己的优缺点，下面我们就来分析分析。

2.2 用顺序表来实现

以下是动态顺序表实现栈的结构体声明和图示：

typedef struct StackList
{
    STDataType* a; //指向动态开辟的空间
    int top; //栈顶所在下标，相当于元素个数
    int capacity;//顺序表容量
}ST;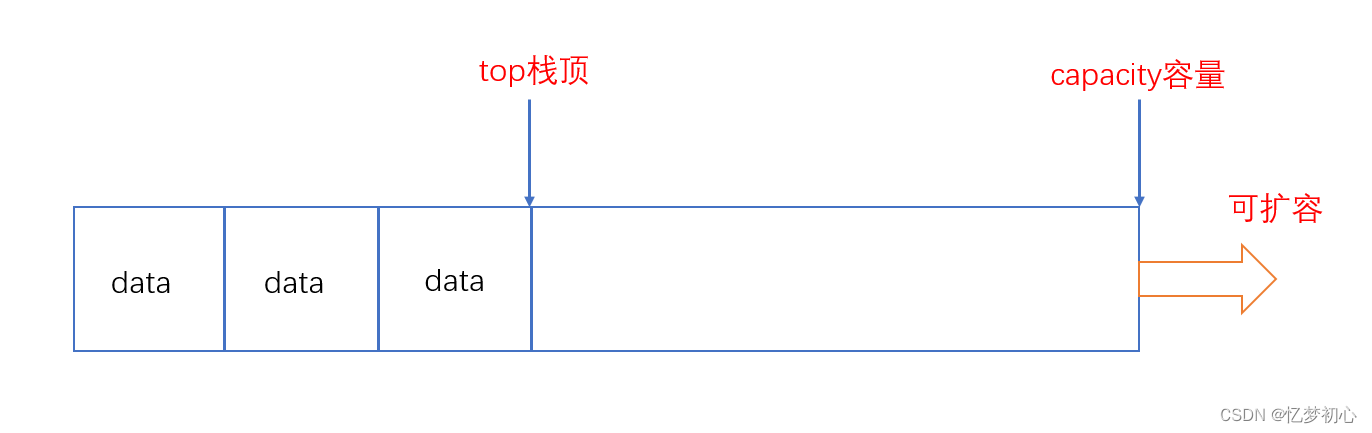

优点：由于栈的插入和删除数据符合 后进先出的原则，我们 把顺序表末端当作栈顶，则插入数据和删除数据就是 尾插和 尾删 。而前面我们知道 顺序表的尾插和尾删效率非常高 ，时间复杂度为O（1）。

缺点： 存在容量限制，当容量不足是需要扩容，扩容需要成本。

2.3 用链表来实现

2.3.1 单链表实现(尾为栈顶)

typedef struct StackNode
{
    STDataType x;//数据域
    StackNode* nest;//指针域，指向下一结点
}ST;
struct Stack
{
    ST* phead;//指向第一个结点
    ST* tail;//指向尾结点
}

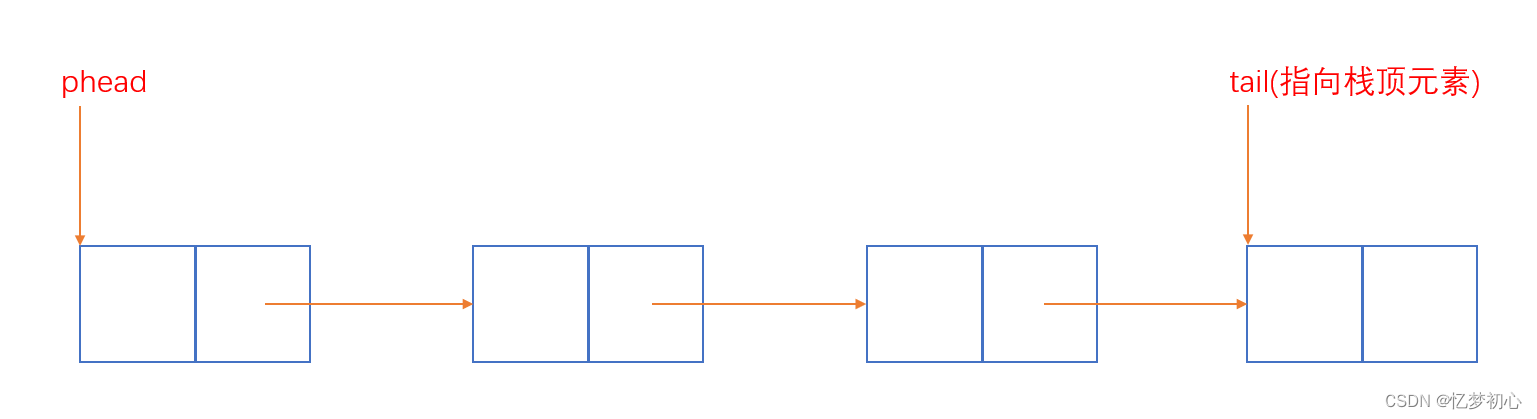
假如我们使用链表尾当作栈顶，则对应的插入删除就是尾插和尾删。我们知道单链表的尾插和尾删要先找到链表尾，时间复杂度是O(N)。可能有人会想，那我定义一个尾指针来记录链表尾部，想法很好，但是这样虽然解决了尾插效率低的问题，但是尾删除了要找到最后一个结点，还要找到其前面的结点，由于链表单向，最终还是要遍历链表，没有什么意义。

2.3.2 单链表实现(头为栈顶)

我们知道，和顺序表相反，单链表头插和头删效率较高，时间复杂度为O（1）。我们就可以将链表头当作栈顶，这样插入就相当于头插，删除就相当于头删，如下：

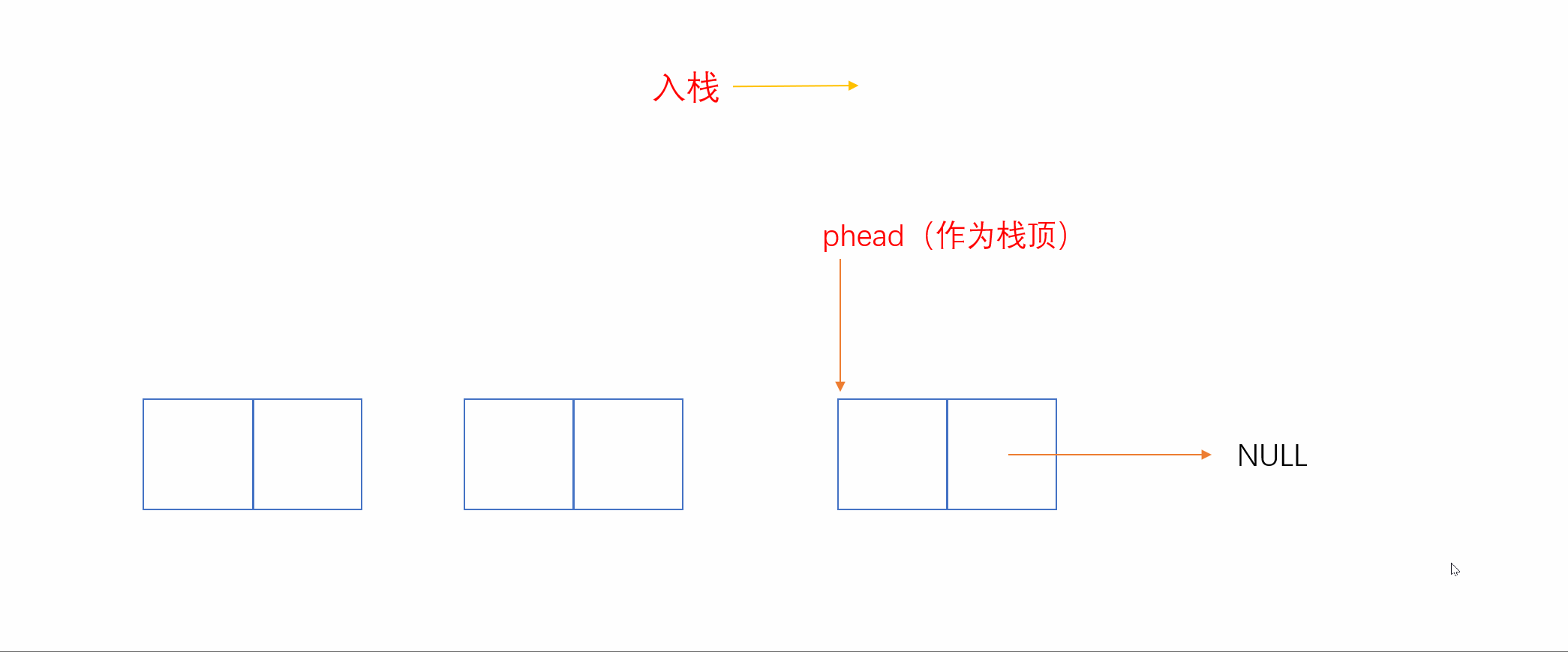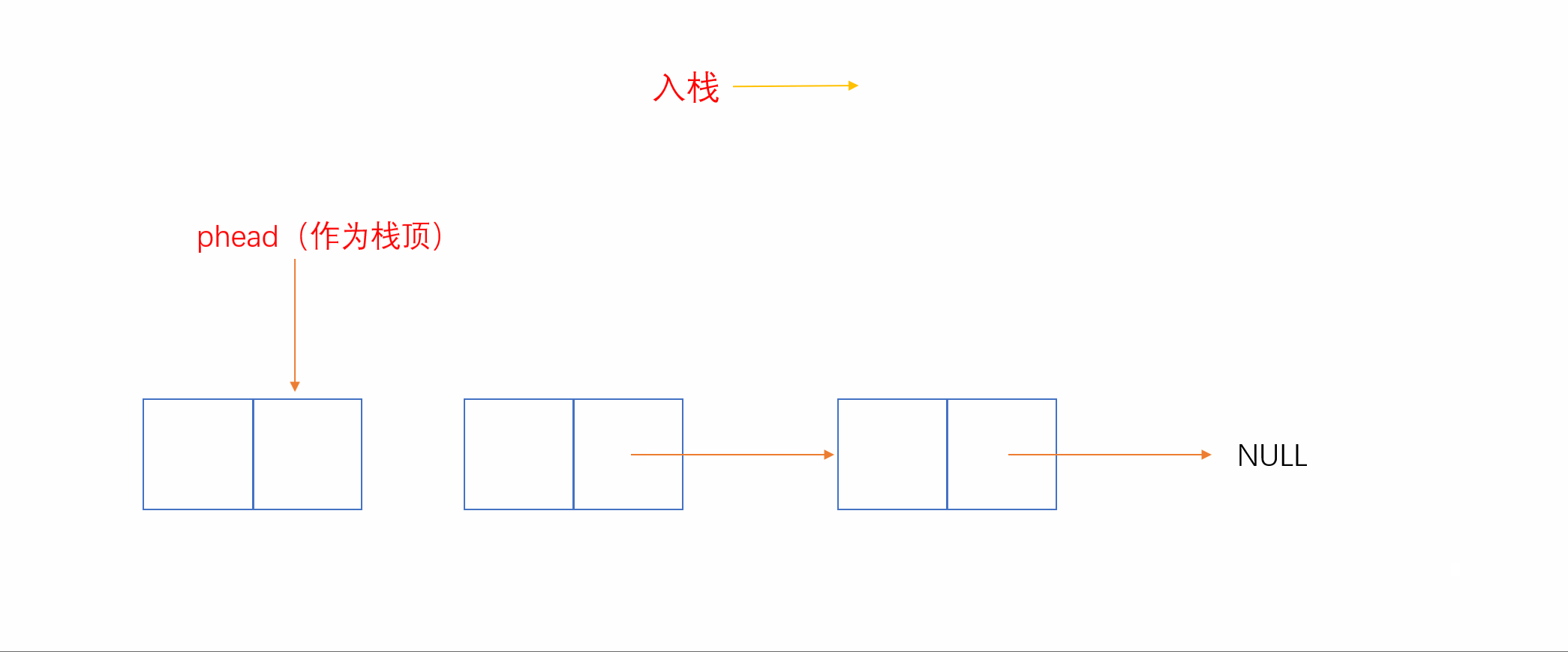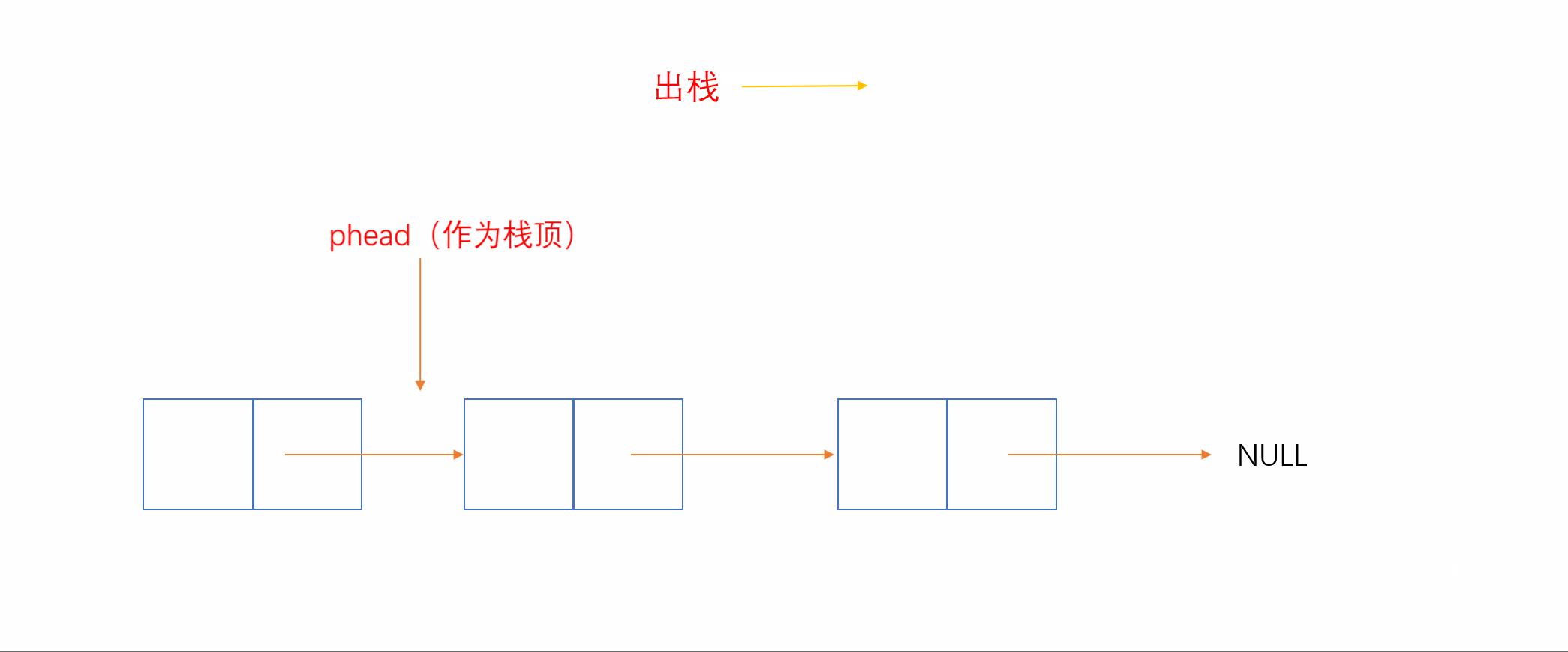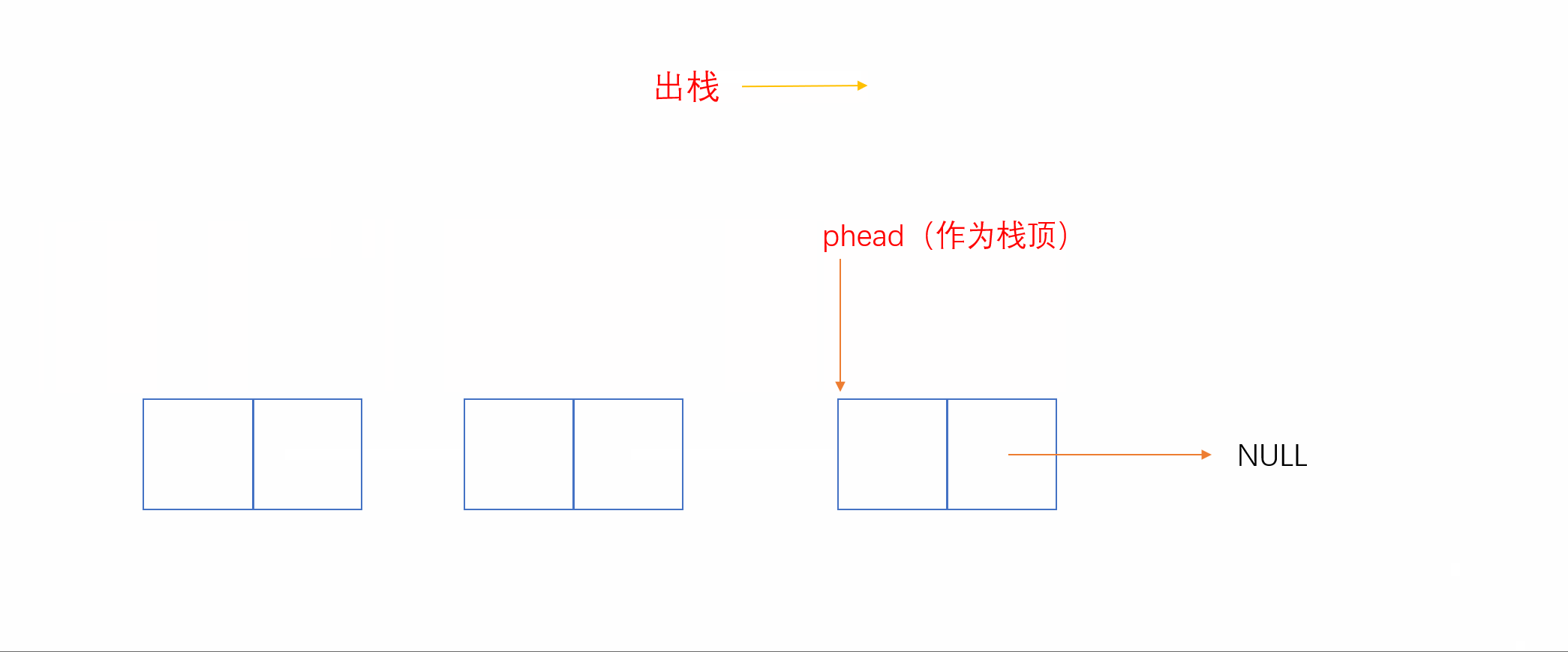
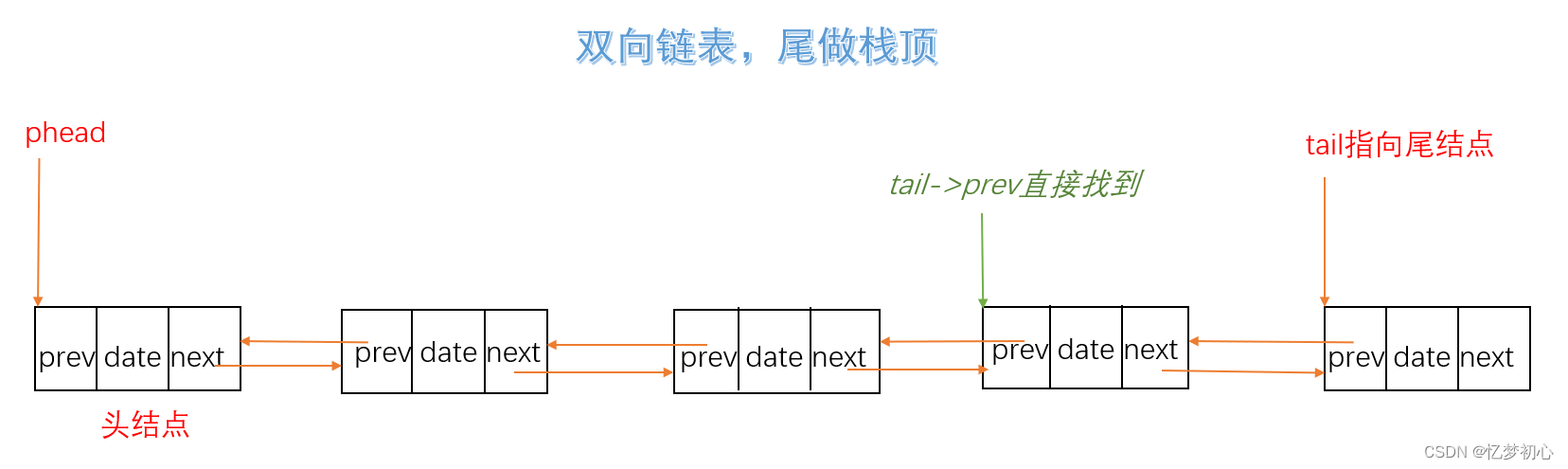
2.3.3 双向链表实现

如果一定要使用链表以及把链表尾当作栈顶，为了解决删除需要找到尾结点的前驱结点时间效率低的问题，我们可以用双向链表来实现栈。双向链表除了后继指针还增加了前驱指针来指向上一个结点，利用这个结构可以直接得到上一个结点，无需再遍历链表，时间复杂度为O（1）。

typedef struct StackNode
{
    STDataType x;//数据域
    StackNode* nest;//后继指针域，指向下一结点
    StackNode* prev;//前驱指针域，指向上一结点
}ST;
struct Stack
{
    ST* phead;//指向第一个结点
    ST* tail;//指向尾结点
}

2.3.4 总结

如果 没有要求栈顶的位置，则我们还是使用 单链表来实现，将头作为栈顶。这是因为 双向链表比单链表的结点多占用了一个前驱指针的空间，虽然现代计算机空间已然构不成太大问题，但是能省则省，大伙们懂的 😏。
如果题目要求栈顶在链表尾的话，那还是老老实实用 双向链表实现吧。
使用链表的缺点就是每次插入都要malloc新结点，会消耗一定的时间成本。

2.4 选择

我们推荐采用 顺序表来实现对栈的操作，原因如下：
1. 栈的特性完美避开了顺序表尾插尾删效率过低的问题，虽然需要扩容，但是链表创建结点也同样需要成本，而 顺序表扩容频率不像链表一样如此频繁。
2. 我们知道CPU与主存速度上存在巨大差距，为了提高效率，CPU和主存之间还存在着 cache高速缓存。 CPU访问cache的速度是快于主存的。每次CPU取数据时会访问cache看看存不存在所需的数据，如果不存在才会访问主存，然后将数据所在的内存块加载到cache中。由于顺序表空间是连续的，根据cache的 空间局部性原理，采用顺序表 cache的命中率会高于链表，效率高。

三. 接口的实现✈

3.1 栈的声明

本文我们采用动态顺序表来实现栈，结构体的声明如下： 
typedef int STDataType;
typedef struct StackList
{
    STDataType* a;//指向动态开辟的空间
    int top; //栈顶所在下标，相当于元素个数
    int capacity;//栈的容量
}ST;

和前面链表顺序表一样，我们不直接指定数据的类型，而是将类型重定义为STDataType，这样做有利于提高代码的可维护性。

3.2 初始化和销毁

和其他数据结构一样，当我们使用栈结构之前需要对其进行初始化，当我们不再使用它是要对它进行销毁，具体代码如下：

//初始化栈
void StackInit(ST* ps)  //需要改变实参，传指针
{
    assert(ps);//确保传入的指针不为空
    ps->a = (STDataType*)malloc(4 * sizeof(STDataType));//起初先分配四个字节空间
    ps->capacity = 4;
    ps->top = 0;
}

//销毁栈
void StackDestroy(ST* ps)
{
    assert(ps);
    free(ps->a);//将栈空间释放掉
    //将栈结构中的信息清空
    ps->capacity = 0;
    ps->top = 0;
    ps->a = NULL;
}

3.3 入栈

由于栈只允许在固定的一端插入，我们又将末端当作栈顶，因此入栈就是尾插。而顺序表的尾插我们已经很清楚了，往栈顶所在下标放入数据，然后栈顶下标加1即可。效果和代码如下：

//入栈
void StackPush(ST* ps, STDataType x)
{
    assert(ps);
    if (ps->top == ps->capacity) //元素个数等于容量，栈满了，先扩容
    {
        STDataType* temp = (STDataType*)realloc(ps->a, 2 * ps->capacity*sizeof(STDataType));
        if (temp == NULL)//失败则退出程序
        {
            printf("扩容失败\n");
            exit(-1);
        }
        else
        {
            ps->a = temp;
            ps->capacity *= 2;
            temp = NULL;
        }
    }
    (ps->a)[ps->top] = x;//入栈
    (ps->top)++;//更新栈顶位置
}

3.4 出栈

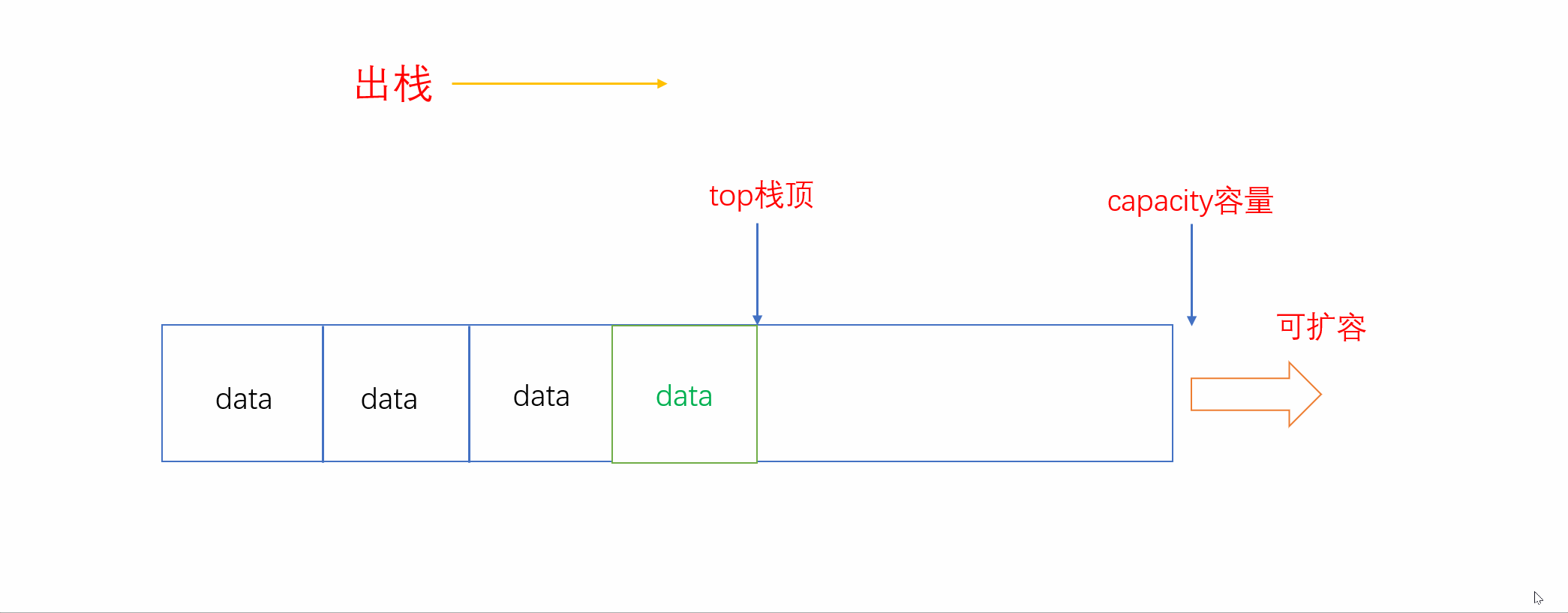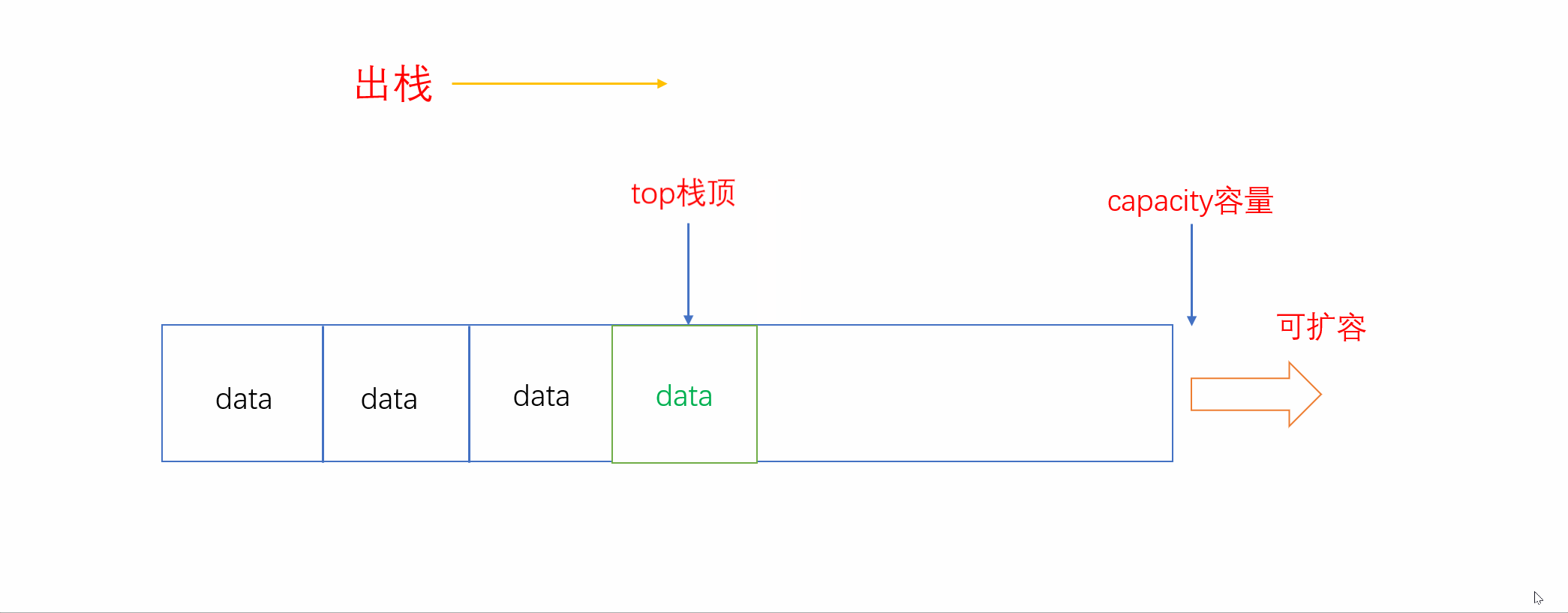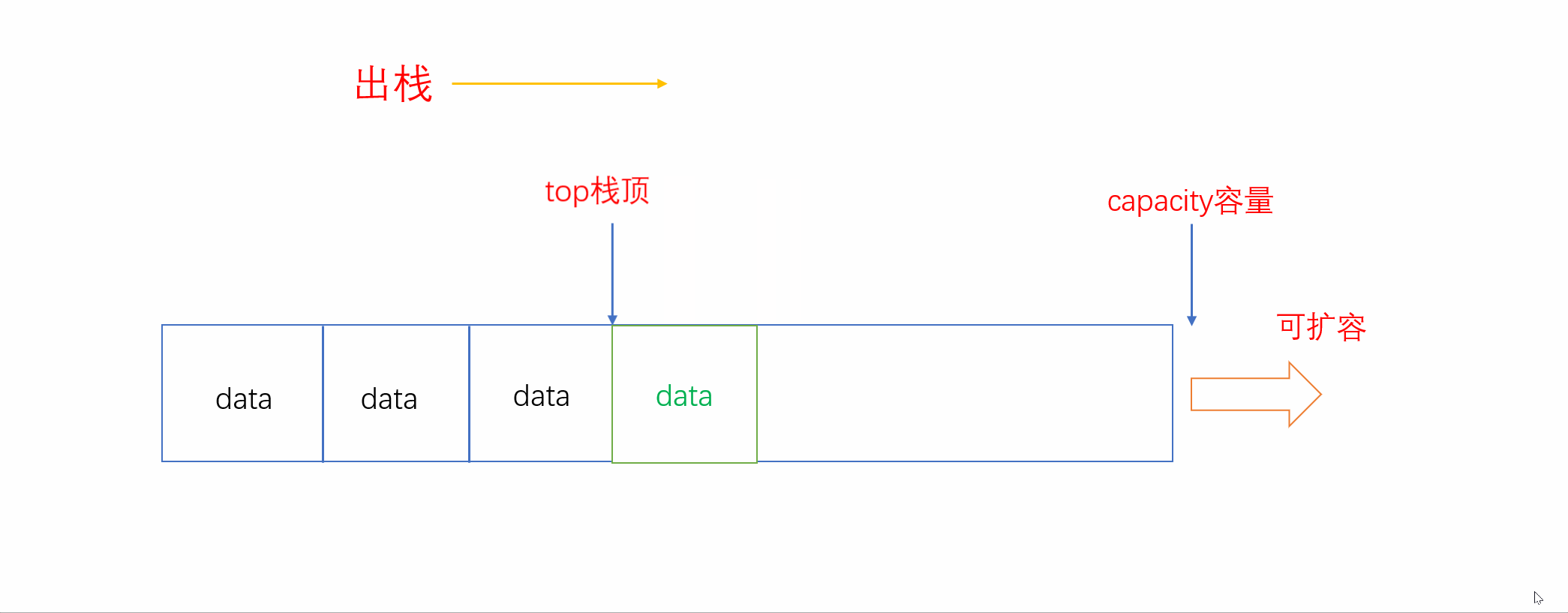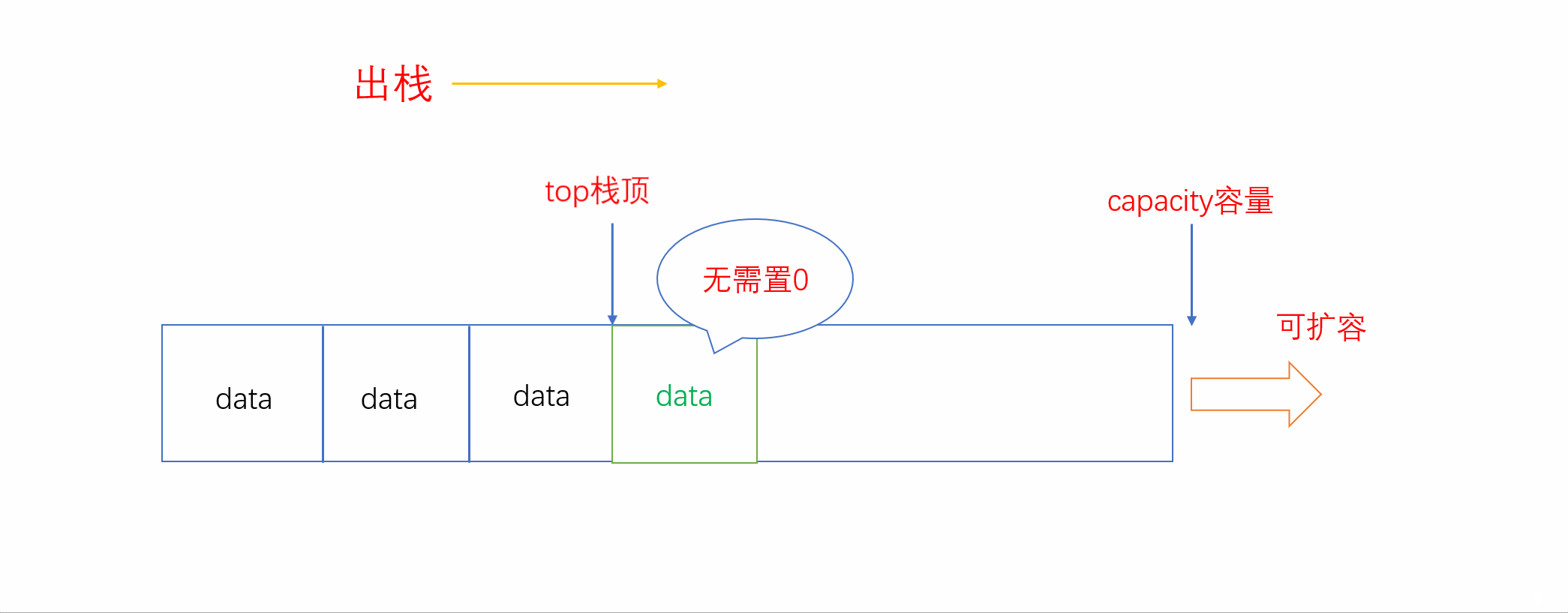
和入栈一样，出栈也只在固定的一端进行。入栈是尾插，则出栈就是尾删。而我们用顺序表来实现栈，因此尾删只需要将栈顶退后一位即可。

这里有人可能会将栈顶的元素置0然后再将栈顶位置后退一位。实际上这种方法并不可取，有以下两种原因：
1. 如果栈顶的元素本身就是0，那我们的行为就失去了意义。
2. 栈的元素类型不一定是整形，如果是浮点型或者结构体，我们赋值为0显然是不妥的。 
//出栈
void StackPop(ST* ps)
{
    assert(ps);//确保传入指针不为空
    assert(ps->top);//确保栈存在元素
    (ps->top)--;//更新栈顶
}

3.5 求栈顶元素

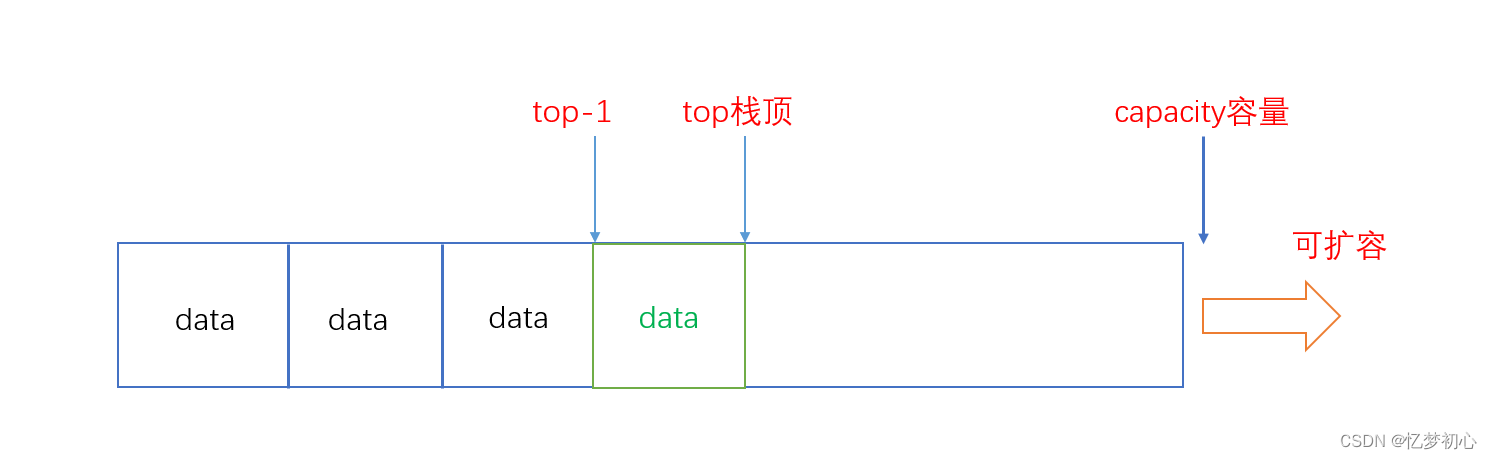
很简单，我们可以直接根据栈顶所在的下标得到栈顶元素，如下：

//求栈顶元素
STDataType StackTop(ST* ps)
{
    assert(ps);
    assert(ps->top);//确保栈中存在元素
    return ps->a[ps->top - 1];//栈顶元素所在下标即为top-1
}

3.6 判空

在我们设计的栈结构中，top实际上就等价于元素个数，通过判断top是否为0就可以知道栈是否为空。我们使用了C语言stdbool.h头文件中的bool类型，其只能用来存放true(1)和false(0)两个值，分别代表真和假。代码如下：

//判空
bool StackEmpty(ST* ps)
{
    assert(ps);
    return ps->top;//top为0则返回false，不为零返回true
}

3.7 求栈的元素个数

根据我们构造的栈结构体，栈顶top的值就是栈的元素个数，直接返回即可：

//求栈的元素个数
int StackSize(ST* ps)
{
    assert(ps);
    return ps->top;
}

3.8 思考

会不会有人会有以下思考：
1. 求栈顶元素，判空，求元素个数都是用一行直接返回，这些接口会不会有些许多余，直接访问结构体相应成员不就好了？
2. 为什么没有实现查找，打印，修改等接口？

下面我们来分析一下：

  • 我们要知道，数据结构的实现方式多种多样，在本文我们将栈元素个数作为栈顶的下标，那可不可以将最后一个元素的下标作为栈顶下标呢？实际上完全可以。那么就会出现一个问题，如果我们使用别人已经封装好的栈，我们要怎么知道栈顶元素下标是top还是top-1呢？我们要怎么知道是top=0为空还是top=-1为空呢？我们要怎么知道元素个数是top还是top+1呢？我们完全不知道，只有设计者才知道，因此设计者往往会将这些功能再封装成函数，供我们直接调用。

  • 这是因为栈是一种限制型数据结构，其不支持随机访问，只允许在固定的一端(栈顶)进行插入和删除操作，不允许在其他的位置进行任何操作。因此，栈不存在查找，打印，修改等对除栈顶之外的位置进行操作的接口，否则会破坏栈的特性。为了遵循栈的特性，我们就不实现这些接口。

四. 完整代码及效果展示🌠

按照以往惯例，我们采用多文件编写的形式，将上述接口的定义实现放在Stack.c文件中，然后将接口的声明和结构体的定义放于Stack.h头文件中，以达到封装的效果。这样我们如果需要使用栈，就只需要在文件中包含对应的头文件Stack.h就可以使用我们上面定义的各种接口。以下为本文实现的栈完整代码以及效果展示：

//Stack.h文件，用于声明接口函数，定义结构体
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int STDataType;
typedef struct StackList
{
    STDataType* a;//指向动态开辟的空间
    int top; //栈顶所在下标，相当于元素个数
    int capacity;//栈的容量
}ST;

//初始化
void StackInit(ST* ps);
//销毁
void StackDestroy(ST* ps);
//出栈
void StackPop(ST* ps);
//入栈
void StackPush(ST* ps, STDataType x);
//求栈顶元素
STDataType StackTop(ST* ps);
//求栈元素个数
int StackSize(ST* ps);
//判空
bool StackEmpty(ST* ps);
//Stack.c文件，用于定义接口函数
#include"Stack.h"

//初始化栈
void StackInit(ST* ps)  //需要改变实参，传指针
{
    assert(ps);//确保传入的指针不为空
    ps->a = (STDataType*)malloc(4 * sizeof(STDataType));//起初先分配四个字节空间
    ps->capacity = 4;
    ps->top = 0;
}

//入栈
void StackPush(ST* ps, STDataType x)
{
    assert(ps);
    if (ps->top == ps->capacity) //元素个数等于容量，栈满了，先扩容
    {
        STDataType* temp = (STDataType*)realloc(ps->a, 2 * ps->capacity * sizeof(STDataType));
        if (temp == NULL)//失败则退出程序
        {
            printf("扩容失败\n");
            exit(-1);
        }
        else
        {
            ps->a = temp;
            ps->capacity *= 2;
            temp = NULL;
        }
    }
    (ps->a)[ps->top] = x;//入栈
    (ps->top)++;//更新栈顶位置
}


//出栈
void StackPop(ST* ps)
{
    assert(ps);//确保传入指针不为空
    assert(ps->top);//确保栈存在元素
    (ps->top)--;//更新栈顶
}

//求栈顶元素
STDataType StackTop(ST* ps)
{
    assert(ps);
    assert(ps->top);//确保栈中存在元素
    return ps->a[ps->top - 1];//栈顶元素所在下标即为top-1
}

//求栈的元素个数
int StackSize(ST* ps)
{
    assert(ps);
    return ps->top;
}


//判空
bool StackEmpty(ST* ps)
{
    assert(ps);
    return ps->top;//top为0则返回false，不为零返回true
}

//销毁栈
void StackDestroy(ST* ps)
{
    assert(ps);
    free(ps->a);//将栈空间释放掉
    //将栈结构中的信息清空
    ps->capacity = 0;
    ps->top = 0;
    ps->a = NULL;
}

最后， 我们在tesst.c文件调用栈各个接口进行测试，如下：

//test.c文件，用于测试
#include"Stack.h"

void test01()
{
    ST s1;
    //初始化
    StackInit(&s1);
    //求元素个数
    printf("入栈前栈的元素个数为:%d\n", StackSize(&s1));
    //入栈
    StackPush(&s1,1);
    StackPush(&s1, 2);
    StackPush(&s1, 3);
    StackPush(&s1, 4);
    printf("入栈后栈的元素个数为:%d\n", StackSize(&s1));
    //由于无法遍历打印，我们就交替使用 求栈顶元素-出栈 来显示栈中元素
    printf("栈中元素:> ");
    while (StackEmpty(&s1))//栈不为空则继续
    {
        //求栈顶元素
        printf("%d ", StackTop(&s1));
        //出栈
        StackPop(&s1);
    }
    //全部出栈
    printf("\n全部出栈后栈的元素个数为:%d\n", StackSize(&s1));
    //销毁
    StackDestroy(&s1);
}

int main()
{
    test01();
    return 0;
}

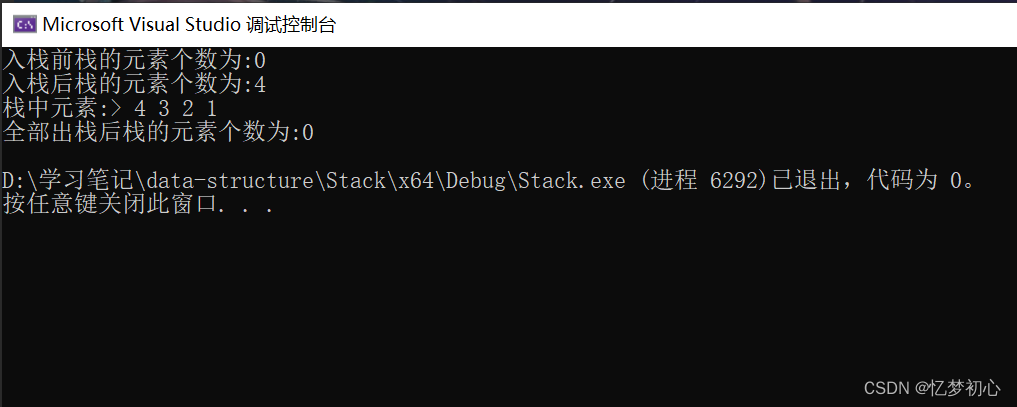
以下是测试的最终效果：

以上，就是本期的全部内容啦🌸

制作不易，能否点个赞再走呢🙏

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/401641.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

怎么把pdf转换成图片?这个方法你值得拥有

怎么把pdf转换成图片?这个方法你值得拥有

想要高效率的工作&#xff0c;除了需要大家合理安排时间之外&#xff0c;一些能够辅助高效工作的工具也是必不可少的。就拿要把一份pdf文件转换成若干图片来说&#xff0c;如果不知道方法&#xff0c;找不到合适的转换工具&#xff0c;那么想要完成这一任务&#xff0c;势必要花…
阅读更多...
万里长征——基础IO

万里长征——基础IO

目录 文件常识 回顾C语言的文件操作 系统层面的文件操作 文件操作的本质 文件fd的分配规则及重定向 linux下一切皆文件 详谈缓冲区问题 文件常识 1、文件 文件内容 文件属性 2、空文件也要在磁盘上占据空间。因为空文件虽然内容为空&#xff0c;但它的属性也会占据空…
阅读更多...
JVM学习笔记十：执行引擎

JVM学习笔记十：执行引擎

0. 前言 声明&#xff1a; 感谢尚硅谷宋红康老师的讲授。 感谢广大网友共享的笔记内容。 B站&#xff1a;https://www.bilibili.com/video/BV1PJ411n7xZ 本文的内容基本来源于宋老师的课件&#xff0c;其中有一些其他同学共享的内容&#xff0c;也有一些自己的理解内容。 1. …
阅读更多...
设计模式——工厂方法模式（创建型）

设计模式——工厂方法模式（创建型）

创建型模式提供了创建对象的机制&#xff0c;能够提升已有代码的灵活性和可复用性。一、工厂方法工厂方法模式是一种创建型设计模式&#xff0c;其在父类中提供一个创建对象的方法&#xff0c;允许子类决定实例化对象的类型。问题&#xff1a;假设你正在开发一款物流管理应用。…
阅读更多...
STA环境

STA环境

目录1. CMOS逻辑门2. 波形3. 时钟3.1. 指定时钟create_clock时钟延迟set_clock_latency 时钟不确定度set_clock_uncertainty 跨时钟域set_false_path3.2. 衍生时钟3.3. 虚拟时钟4. 时序路径2.1. 输入路径2.2. 输出路径2.3. 点对点约束本文介绍在执行静态时序分析&#xff08;St…
阅读更多...
顺序表的基本操作

顺序表的基本操作

目录 一.什么是顺序表 二.顺序表的基本操作 1.初始化 2.增容 3.尾插 4.头插 5.尾删 6.头删 7.指定位置插入 8.指定位置删除 9.打印 10.查找 11.销毁 一.什么是顺序表 顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构&#xff0c;一般情况下采用数组…
阅读更多...
IBMMQ教程二（window版安装）

IBMMQ教程二（window版安装）

下载下载地址&#xff1a;https://public.dhe.ibm.com/ibmdl/export/pub/software/websphere/messaging/mqadv/我这里选择的是9.1.0.0版本安装将下载完成的压缩包解压双击Setup.exe直接运行点击软件需求查看系统配置是否满足&#xff0c;右边绿色的对号说明满足需求&#xff0c…
阅读更多...
linux 端口查询命令

linux 端口查询命令

任何知识都是用进废退&#xff0c;有段时间没摸linux&#xff0c;这大脑里的知识点仿佛全部消失了&#xff0c;就无语。 索性&#xff0c;再写一篇记录&#xff0c;加强一下记忆&#xff0c;下次需要就看自己的资料好了。lsof命令Linux端口查询命令可以通过lsof实现&#xff1a…
阅读更多...
教育小程序开发解决方案

教育小程序开发解决方案

如今无论是国家还是家庭对于教育的重视性也越来越高&#xff0c;都希望自己的孩子能够赢在起跑线上&#xff0c;但是因为工作的缘故许多家长并没有过多的精力去辅导孩子学习&#xff0c;再加上许多家长对于教育也并没有经验与技巧。而这些都充分体现了正确教育的重要性。 那么一…
阅读更多...
2023金三银四常见Handler面试总结，附带答案

2023金三银四常见Handler面试总结，附带答案

以下的Handler的面试题都是在面试过程中总结出来比较常见的面试题&#xff0c;现在分享给大家&#xff0c;希望可以帮助你们&#xff01;1.Handler的实现原理从四个方面看Handler、Message、MessageQueue 和 Looper Handler:负责消息的发送和处理 Message:消息对象&#xff0c;…
阅读更多...
FL Studio21最新中文版下载及切换语言教程

FL Studio21最新中文版下载及切换语言教程

随着近年来摇滚、电音的发展&#xff0c;越来越多的人开始对电子音乐编曲感兴趣&#xff0c;而电音编曲的首要条件&#xff0c;就是需要一个好的DAW&#xff08;数字音频工作站&#xff09;&#xff0c;常用的DAW有很多&#xff0c;例如Cubase、Nuendo、Pro Tools、 SONAR等等&…
阅读更多...
Unity - 搬砖日志 - Texture.mipmapBias 无效的解决方法

Unity - 搬砖日志 - Texture.mipmapBias 无效的解决方法

文章目录环境原因解決方案Referenes环境 Unity : 2020.3.37f1 Pipeline : BRP 原因 因为美术发现有些贴图太糊&#xff0c;但是经过研究发现&#xff0c;mipmap0就是完全够精度的 但是不可能还要提升贴图的尺寸&#xff0c;因为经过多方咨询&#xff08;咨询TA大佬&#xff0…
阅读更多...
2023 年会是网络安全的关键年吗？

2023 年会是网络安全的关键年吗？

过去 12 个月对网络安全领域和周围的每个人来说再次充满挑战。和往年不同&#xff0c;感觉很不一样&#xff0c;攻击源源不断。过去&#xff0c;大型漏洞每季度发生一次&#xff0c;但在过去一年中&#xff0c;在某些情况下&#xff0c;我们几乎每周都会处理严重漏洞。 已知利…
阅读更多...
itop-3568开发板驱动学习笔记（7）高级字符设备（一）阻塞 IO 和 非阻塞 IO

itop-3568开发板驱动学习笔记（7）高级字符设备（一）阻塞 IO 和 非阻塞 IO

《【北京迅为】itop-3568开发板驱动开发指南.pdf》 学习笔记 文章目录阻塞 IO非阻塞 IOIO 实验&#xff08;使用等待队列&#xff09;等待队列阻塞 IO 实验非阻塞 IO 实验阻塞 IO I/O输入/输出(Input/Output)&#xff0c;分为IO设备和IO接口两个部分。 在POSIX兼容的系统上&…
阅读更多...
python学习——【第四弹】

python学习——【第四弹】

前言 上一篇文章 python学习——【第三弹】 中学习了python中的流程控制语句&#xff0c;这篇文章我们接着学习python中的序列。先给大家介绍不可变序列 字符串和可变序列 列表&#xff0c;下一篇文章接着补充元组&#xff0c;集合和字典。 序列 指的是一块可以存放多个值的…
阅读更多...
多线程的风险 --- 线程安全

多线程的风险 --- 线程安全

✨个人主页&#xff1a;bit me&#x1f447; ✨当前专栏&#xff1a;Java EE初阶&#x1f447; ✨每日一语&#xff1a;低头赶路&#xff0c;敬事如仪&#xff1b;自知自心&#xff0c;其路则明。 目 录&#x1f378;一. 线程不安全&#x1f379;二. 线程不安全的原因&#x1f…
阅读更多...
【C语言】每日刷题 —— 牛客语法篇（1）

【C语言】每日刷题 —— 牛客语法篇（1）

前言 大家好&#xff0c;今天带来一篇新的专栏c_牛客&#xff0c;不出意外的话每天更新十道题&#xff0c;难度也是从易到难&#xff0c;自己复习的同时也希望能帮助到大家&#xff0c;题目答案会根据我所学到的知识提供最优解。 &#x1f3e1;个人主页&#xff1a;悲伤的猪大…
阅读更多...
Java的jar包打包成exe应用

Java的jar包打包成exe应用

将springboot项目使用maven打出的jar包&#xff0c;打成windows平台下exe应用程序包&#xff08;自带jre环境&#xff09;。 工具&#xff1a;1、exe4j 2、Inno Setup 工具放到网盘&#xff0c;链接&#xff1a;https://pan.baidu.com/s/1ZHX8P7u-7GBxaC6uaIC8Ag 提取码&#x…
阅读更多...
VMware16pro虚拟机安装全过程

VMware16pro虚拟机安装全过程

很多时候需要用到Linux系统&#xff0c;简单的一种方式可以是&#xff1a;Windows系统运行Linux&#xff08;Windows Subsystem for Linux&#xff09;不过有些时候还是需要虚拟机来运行Linux&#xff0c;也更方便点&#xff0c;比如在做嵌入式系统的烧录等操作都需要Linux环境…
阅读更多...
人的高级认知：位置感

人的高级认知：位置感

你知道吗&#xff1f;人有个高级认知&#xff1a;位置感 位置感是啥&#xff1f;咋提高位置感&#xff1f; 趣讲大白话&#xff1a;知道自己几斤几两 【趣讲信息科技99期】 ******************************* 位置感 就是对自己所处环境和自身存在的领悟 属于人生智慧 来源于阅历…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023