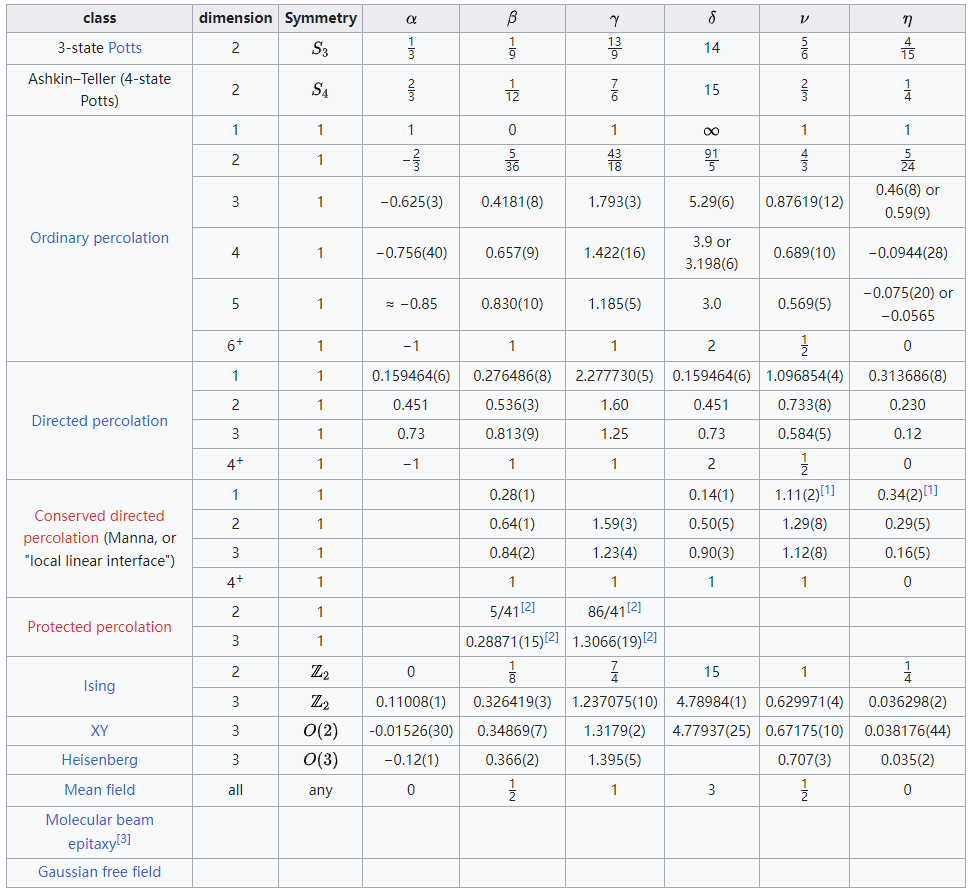
优化器Optimizer
什么是优化器
pytorch的优化器:管理并更新模型中可学习参数的值,使得模型输出更接近真实标签
导数:函数在指定坐标轴上的变化率
方向导数:指定方向上的变化率(二元及以上函数,偏导数)
梯度:一个向量,方向是使得方向导数取得最大值的方向
Pytorch的Optimizer

参数
- defaults:优化器超参数
- state:参数的缓存,如momentum的缓存
param_groups:管理的参数组- _step_count:记录更新次数,学习率调整中使用
基本方法:
- zero_grad():清空所管理参数的梯度

pytorch特性:张量梯度不会自动清零
-
step():执行一步更新
-
add_param_group():添加参数组

-
state_dict():获取优化器当前状态信息字典

-
load_state_dict():加载状态信息字典
使用代码帮助理解和学习
import os
import torch
import torch.optim as optim
BASE_DIR = os.path.dirname(os.path.abspath(__file__))
weight = torch.randn((2, 2), requires_grad=True)
weight.grad = torch.ones((2, 2))
# 需要传入一个可迭代对象
optimizer = optim.SGD([weight], lr=1)
print("weight before step:{}".format(weight.data))
optimizer.step()
print("weight after step:{}".format(weight.data))
weight before step:tensor([[-0.0606, -0.3197],
[ 1.4949, -0.8007]])
weight after step:tensor([[-1.0606, -1.3197],
[ 0.4949, -1.8007]])
weight = weight - lr * weight.grad
上面学习率是1,把学习率改为0.1试一下
optimizer = optim.SGD([weight], lr=0.1)
weight before step:tensor([[ 0.3901, 0.2167],
[-0.3428, -0.7151]])
weight after step:tensor([[ 0.2901, 0.1167],
[-0.4428, -0.8151]])
接着上面的代码,我们再看一下add_param_group方法
# add_param_group方法
print("optimizer.param_groups is \n{}".format(optimizer.param_groups))
w2 = torch.randn((3, 3), requires_grad=True)
optimizer.add_param_group({"params": w2, "lr": 0.0001})
print("optimizer.param_groups is\n{}".format(optimizer.param_groups))
optimizer.param_groups is
[{'params': [tensor([[ 0.1749, -0.2018],
[ 0.0080, 0.3517]], requires_grad=True)], 'lr': 0.1, 'momentum': 0, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}]
optimizer.param_groups is
[{'params': [tensor([[ 0.1749, -0.2018],
[ 0.0080, 0.3517]], requires_grad=True)], 'lr': 0.1, 'momentum': 0, 'dampening': 0, 'weight_decay': 0, 'nesterov': False},
{'params': [tensor([[ 0.4538, -0.8521, -1.3081],
[-0.0158, -0.2708, 0.0302],
[-0.3751, -0.1052, -0.3030]], requires_grad=True)], 'lr': 0.0001, 'momentum': 0, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}]
关于zero_grad()、step()、state_dict()、load_state_dict()这几个方法比较简单就不再赘述。
SGD随机梯度下降
learning_rate学习率

这里学习率为1,可以看到并没有达到梯度下降的效果,反而y值越来越大,这是因为更新的步伐太大。

我们以y = 4*x^2这个函数举例,将y值作为要优化的损失值,那么梯度下降的过程就是为了找到y的最小值(即此函数曲线的最小值);如果我们把学习率设置为0.2,就可以得到这样一个梯度下降的图
def func(x):
return torch.pow(2*x, 2)
x = torch.tensor([2.], requires_grad=True)
iter_rec, loss_rec, x_rec = list(), list(), list()
lr = 0.2
max_iteration = 20
for i in range(max_iteration):
y = func(x)
y.backward()
print("iter:{}, x:{:8}, x.grad:{:8}, loss:{:10}".format(
i, x.detach().numpy()[0], x.grad.detach().numpy()[0], y.item()
))
x_rec.append(x.item())
x.data.sub_(lr * x.grad)
x.grad.zero_()
iter_rec.append(i)
loss_rec.append(y.item())
plt.subplot(121).plot(iter_rec, loss_rec, '-ro')
plt.xlabel("Iteration")
plt.ylabel("Loss value")
x_t = torch.linspace(-3, 3, 100)
y = func(x_t)
plt.subplot(122).plot(x_t.numpy(), y.numpy(), label="y = 4*x^2")
plt.grid()
y_rec = [func(torch.tensor(i)).item() for i in x_rec]
plt.subplot(122).plot(x_rec, y_rec, '-ro')
plt.legend()
plt.show()

这里其实存在一个下降速度更快的学习率,那就是0.125,一步就可以将loss更新为0,这是因为我们已经了这个函数表达式,而在实际神经网络模型训练的过程中,是不知道所谓的函数表达式的,所以只能选取一个相对较小的学习率,然后以训练更多的迭代次数来达到最优的loss。

动量(Momentum,又叫冲量)
结合当前梯度与上一次更新信息,用于当前更新
为什么会出现动量这个概念?
当学习率比较小时,往往更新比较慢,通过引入动量,使得后续的更新受到前面更新的影响,可以更快的进行梯度下降。
指数加权平均:当前时刻的平均值(Vt)与当前参数值(θ)和前一时刻的平均值(Vt-1)的关系。

根据上述公式进行迭代展开,因为0<β<1,当前时刻的平均值受越近时刻的影响越大(更近的时刻其所占的权重更高),越远时刻的影响越小,我们可以通过下面作图来看到这一变化。
import numpy as np
import matplotlib.pyplot as plt
def exp_w_func(beta, time_list):
return [(1-beta) * np.power(beta, exp) for exp in time_list]
beta = 0.9
num_point = 100
time_list = np.arange(num_point).tolist()
weights = exp_w_func(beta, time_list)
plt.plot(time_list, weights, '-ro', label="Beta: {}\n = B * (1-B)^t".format(beta))
plt.xlabel("time")
plt.ylabel("weight")
plt.legend()
plt.title("exponentially weighted average")
plt.show()

这里β是一个超参数,设置不同的值,其对于过去时刻的权重计算如下图
beta_list = [0.98, 0.95, 0.9, 0.8]
w_list = [exp_w_func(beta, time_list) for beta in beta_list]
for i, w in enumerate(w_list):
plt.plot(time_list, w, label="Beta: {}".format(beta_list[i]))
plt.xlabel("time")
plt.ylabel("weight")
plt.legend()
plt.show()

从图中可以得到这一结论:β值越小,记忆周期越短,β值越大,记忆周期越长。
pytorch中带有momentum参数的更新公式

对于y=4*x^2这个例子,在没有momentum时,我们对比学习率分别为0.01和0.03会发现,0.03收敛的更快。

如果我们给learning_rate=0.01增加momentum参数,会发现其可以先一步0.03的学习率到达loss的较小值,但是因为动量较大的因素,在达到了最小值后还会反弹到一个大的值。

Pytorch中的优化器
optim.SGD
主要参数:
params:管理的参数组lr:学习率- momentum:动量系数,贝塔
weight_decay:L2正则化系数nesterov:是否采用NAG,默认False
optim.Adagrad:自适应学习率梯度下降法
optim.RMSprop:Adagrad的改进
optim.Adadelta:Adagrad的改进
optim.Adam:RMSprop结合Momentum
optim.Adamax:Adam增加学习率上限
optim.SparseAdam:稀疏版的Adam
optim.ASGD:随机平均梯度下降
optim.Rprop:弹性反向传播
optim.LBFGS:BFGS的改进
学习率调整
前期学习率大,后期学习率小
pytorch中调整学习率的基类
class _LRScheduler
主要属性:
- optimizer:关联的优化器
- last_epoch:记录epoch数
base_lrs:记录初始学习率
主要方法:
- step():更新下一个epoch的学习率
get_lr():虚函数,计算下一个epoch的学习率
StepLR
等间隔调整学习率
主要参数:
- step_size:调整间隔数
- gamma:调整系数
调整方式:lr = lr * gamma
import torch
import torch.optim as optim
import matplotlib.pyplot as plt
LR = 0.1
iteration = 10
max_epoch = 200
weights = torch.randn((1,), requires_grad=True)
target = torch.zeros((1, ))
optimizer = optim.SGD([weights], lr=LR, momentum=0.9)
scheduler_lr = optim.lr_scheduler.StepLR(optimizer, step_size=50, gamma=0.1) # 设置学习率下降策略
lr_list, epoch_list = list(), list()
for epoch in range(max_epoch):
lr_list.append(scheduler_lr.get_lr())
epoch_list.append(epoch)
for i in range(iteration):
loss = torch.pow((weights-target), 2)
loss.backward()
optimizer.step()
optimizer.zero_grad()
scheduler_lr.step()
plt.plot(epoch_list, lr_list, label='Step LR Scheduler')
plt.xlabel('Epoch')
plt.ylabel('Learning Rate')
plt.legend()
plt.show()

MultiStepLR
功能:按给定间隔调整学习率
主要参数:
- milestones:设定调整时刻数
- gamma:调整系数
调整方式:lr = lr * gamma
# MultiStepLR
milestones = [50, 125, 160]
scheduler_lr = optim.lr_scheduler.MultiStepLR(optimizer, milestones=milestones, gamma=0.1)
只需要改变这里代码,其他部分与StepLR中基本一致

ExponentialLR
功能:按指数衰减调整学习率
主要参数:
- gamma:指数的底
调整方式:lr = lr * gamma ** epoch
# Exponential LR
gamma = 0.95
scheduler_lr = optim.lr_scheduler.ExponentialLR(optimizer, gamma=gamma)

CosineAnnealingLR
功能:余弦周期调整学习率
主要参数:
- T_max:下降周期
- eta_min:学习率下限
调整方式:

# CosineAnnealingLR
t_max = 50
scheduler_lr = optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=t_max, eta_min=0)

ReduceLRonPlateau
功能:监控指标,当指标不再变化则调整学习率
主要参数:
mode:min/max,两种模式,min观察下降,max观察上升- factor:调整系数
- patience:“耐心”,接受几次不变化
cooldown:“冷却时间”,停止监控一段时间- verbose:是否打印日志
min_lr:学习率下限eps:学习率衰减最小值
# Reduce LR on Plateau
loss_value = 0.5
accuray = 0.9
factor = 0.1
mode = 'min'
patience = 10
cooldown = 10
min_lr = 1e-4
verbose = True
scheduler_lr = optim.lr_scheduler.ReduceLROnPlateau(optimizer, factor=factor, mode=mode, patience=patience,
cooldown=cooldown, min_lr=min_lr, verbose=verbose)
for epoch in range(max_epoch):
for i in range(iteration):
optimizer.step()
optimizer.zero_grad()
# if epoch == 5:
# loss_value = 0.4
# 把要监控的指标传进去
scheduler_lr.step(loss_value)
Epoch 12: reducing learning rate of group 0 to 1.0000e-02.
Epoch 33: reducing learning rate of group 0 to 1.0000e-03.
Epoch 54: reducing learning rate of group 0 to 1.0000e-04.
LambdaLR
功能:自定义调整策略
主要参数:
lr_lambda:function or list
# lambda LR
lr_init = 0.1
weights_1 = torch.randn((6, 3, 5, 5))
weights_2 = torch.ones((5, 5))
optimizer = optim.SGD([
{'params': [weights_1]},
{'params': [weights_2]}
], lr=lr_init)
lambda1 = lambda epoch: 0.1 ** (epoch // 20)
lambda2 = lambda epoch: 0.95 ** epoch
scheduler = torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda=[lambda1, lambda2])
lr_list, epoch_list = list(), list()
for epoch in range(max_epoch):
for i in range(iteration):
optimizer.step()
optimizer.zero_grad()
scheduler.step()
lr_list.append(scheduler.get_lr())
epoch_list.append(epoch)
print('epoch: {:5d}, lr:{}'.format(epoch, scheduler.get_lr()))