目录

1.BN的问题

1.1 BN与batch size

1.2 BN与RNN

 2.LN详解

2.1 MLP中的LN

2.2 RNN中的LN

2.3 LN与ICS和损失平面平滑

---

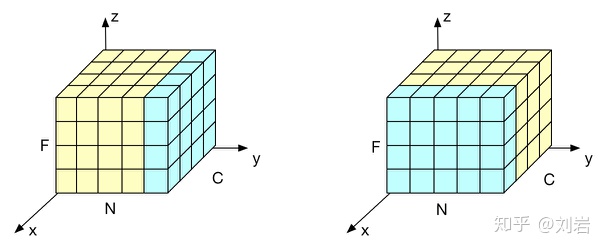
BN不适用于RNN等动态网络和batchsize较小的时候效果不好。LayerNormalization的提出有效的解决BN的这两个问题。LN和BN不同点是归一化的维度是互相垂直的，如图1所示。在图中N表示样本轴，C表示通道轴，F是每个通道的特征数量。BN如右侧所示，它是取不同样本的同一个通道的特征做郭奕华；LN则是如左侧所示，它取得是同一个样本的不同通道做归一化。

1.BN的问题

1.1 BN与batch size

如图1右侧部分，BN是按照样本数计算归一化统计量的，当样本数很少时，比如说只有4个。这四个样本的均值和方差便不能反映全局的统计分布信息，所以基于少量样本的BN的效果会变得很差。在一些场景中，比如说硬件资源受限、在线学习等场景，BN是非常不适用的。

1.2 BN与RNN

RNN可以展开成一个隐藏层共享参数的MLP，随着时间片的增多，展开后的MLP的层数也在增多，最终层数由输入数据的时间片的数量决定，所以RNN是一个动态的网络。

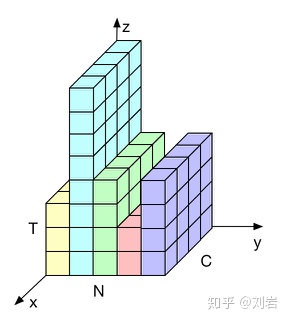
在一个batch中，通常各个样本的长度都是不同的，当统计到比较靠后的时间片时，例如图2中t>4时，这时只有一个样本还有数据，基于这个样本的统计信息不能反映全局分布，所以这时BN的效果并不好。

另外如果在测试时我们遇到了长度大于任何一个训练样本的测试样本，我们无法找到保存的归一化统计量，所以BN无法运行

2.LN详解

2.1 MLP中的LN

通过第一节的分析，我们知道BN的两个缺点的产生原因均是因为计算归一化统计量时计算的样本量太少。LN是一个独立于batch size的算法，所以无论样本数多少都不会影响参与LN计算的数据量，从而解决BN的两个问题。LN的做法如图1左侧所示：根据样本的特征数做归一化。

先看MLP中的LN。设H是一层中隐藏节点的数量，ｌ是MLP的层数，我们计算LN的归一化统计量μ和σ：

注意上面统计量的计算是和样本数量没有关系的，它的数量只取决于隐藏节点的数量，所以只要隐层节点的数量足够多，我们就能保证LN的归一化统计量足够具有代表性。通过可以得到归一化后的值:

在LN中我们也需要一组参数来保证归一化操作不会破坏之前的信息，在LN中这组参数叫做增益(gain)g和偏置(bias) b（等同于BN中的γ和β)，g初始化为1，b初始化为0。假设激活函数为f,最终LN的输出为:

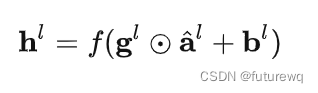
我们将式子合并，并忽略参数l，我们有：

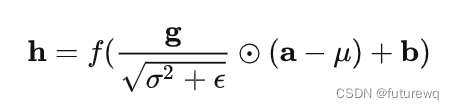
2.2 RNN中的LN

 在RNN中，我们可以非常简单的在每个时间片中使用LN，而且在任何时间片我们都能归一化统计量统计的是H个节点的信息。对于RNN时刻t时的节点，其输入时t-1时刻的隐藏状态和t时刻的输入数据，可以表示为

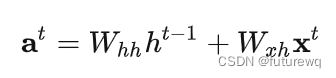
接着我们便可以在上采用同样的归一化过程:

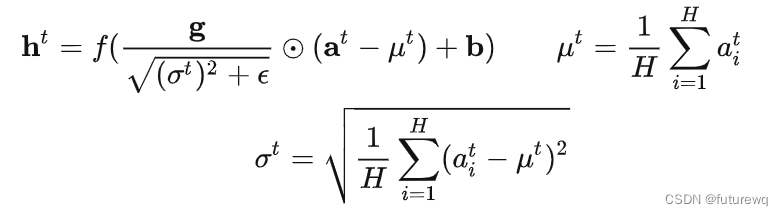
2.3 LN与ICS和损失平面平滑

LN也能减轻ICS，加速收敛速度。LN不需要额外维护一个对训练样本均值方差的统计，每次只需要在句子范围内计算即可。 

模型优化之Layer Normalization - 知乎

层标准化详解（Layer Normalization）_十里清风的博客-CSDN博客