思路

在这里插入图片描述
题目主要的意思在一个升序也就是有序的数组中找到一段相同数组的起始位置和最终位置也就是查找两个数的问题

题目给的是升序数列让人很容易想到二分查找来查找两个数

二分查找

我们此时的问题就转化为查找到这段序列的起始位置和终止位置我们可以用二分查找的方式

左边界

我们可以先找这段序列的左边界

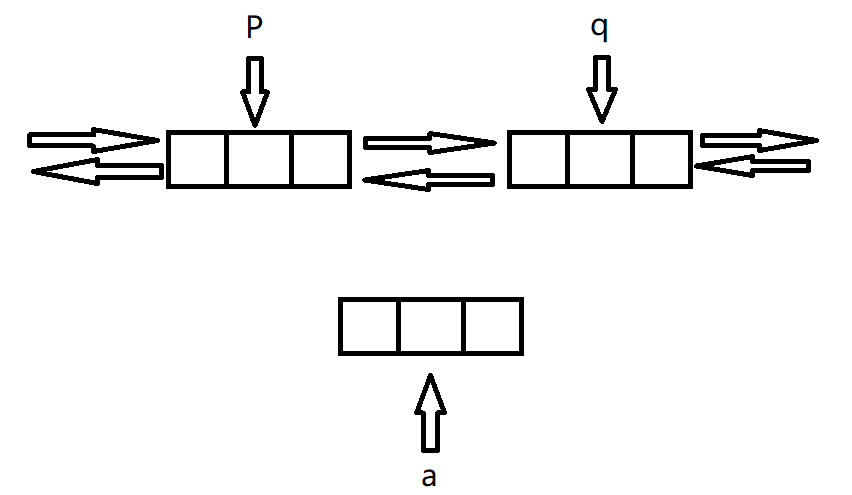
例如下面这段序列

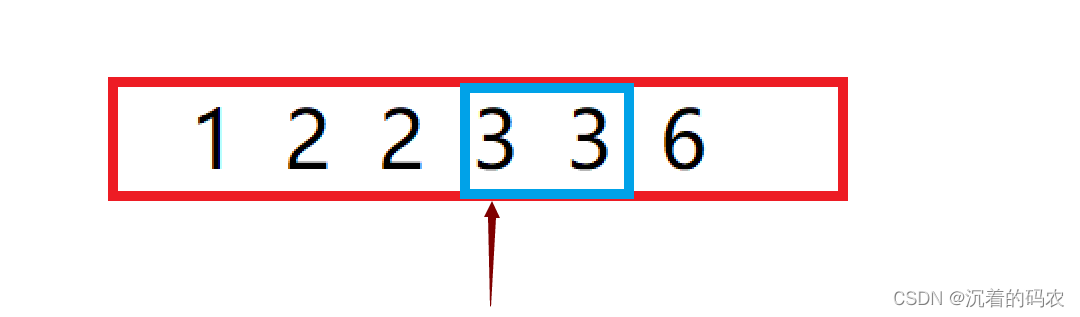
在这里插入图片描述
我们要找到箭头指向的这个数的位置

我们要设置两个标记来标记每一次二分的左右边界
第一次二分定义（l = 0 r = n-1） n为序列的长度
在设置一个 mid 变量来标记序列中间位置

每次二分检查 mid 和我们要找的这个数的大小关系
直到l >= r此时就找到了左边界

int left_bound(int l, int r) {
    while (l < r) {
        int mid = l + r >> 1;//求中间值
        if (q[mid] >= k) r = mid;//更新有边界
        else l = mid + 1;//更新左边界
    }
    return l;
}

我们在这里要尤其注意边界问题因为这一段序列中有重复数据

在查找左边界时如果 q[mid]>=k 条件成立说明左边界点不在右半部分此时要更新右边界的值
但是存在这个点就是我们要找的点的情况 此时mid点就不可以跳过 在更新边界点时就要保留mid点就是 r = mid

但是如果 q[mid]>=k条件不成立这个时候说明左边节点在右半部分此时要更新左半部分
此时这个点不可能是我们要找的点 因为这个点必小于k 所以将l更新为mid+1跳过这个点

右边界

然后来找这段数的右边界
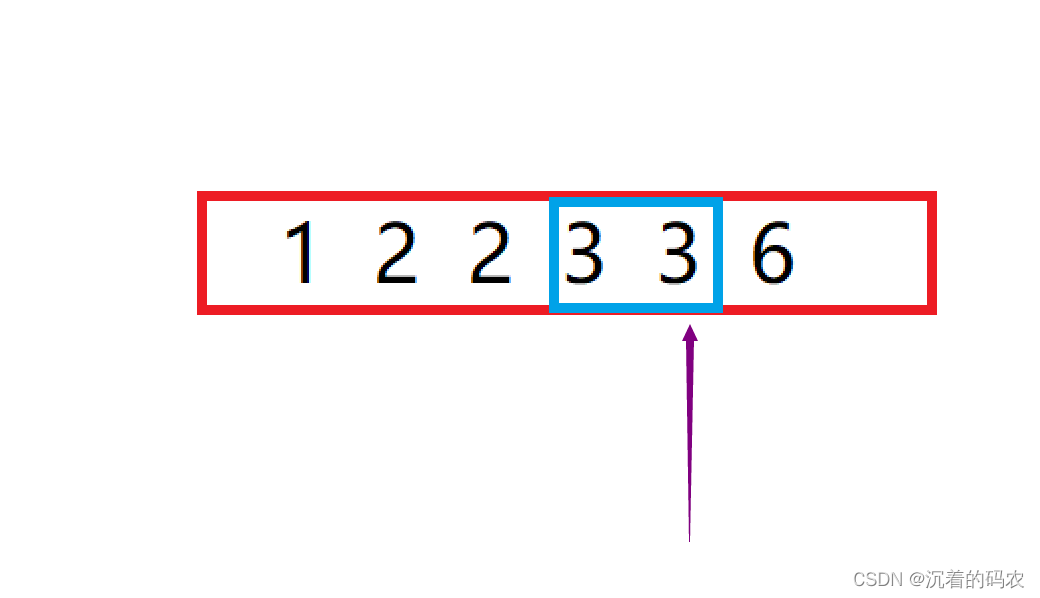
在这里插入图片描述

还是这段序列此时我们要找的是箭头指向的这个数据如果理解了找左边界的情况这个情况也类似

还是
我们要找到箭头指向的这个数的位置
我们要设置两个标记来标记每一次二分的左右边界
第一次二分定义（l = 0 r = n-1） n为序列的长度
在设置一个 mid 变量来标记序列中间位置

每次二分检查 mid 和我们要找的这个数的大小关系
直到l >= r此时就找到了右边界

int right_bound(int l, int r) {
    while (l < r) {
        int mid = l + r + 1 >> 1;
        if (q[mid] <= k) l = mid;
        else r = mid - 1;
    }
    return l;
}

还是和找左边界一样的考虑方法

在查找右边界时如果 q[mid] <= k 条件成立说明右边界点不在左半部分此时要更新左边界的值但是存在q[mid] = k 的情况所以可能会出现mid位置正好是我们要的右边界所以此时保留mid位置的值 l = mid

如果q[mid] <= k条件不成立 说明右边界点不在右半部分此时要更新右边界的值由于此时不可能存在q[mid] = k 的情况出现所以mid位置的值不需要保存 r = mid - 1

注意再求右边界的时候为什么 mid = (l + r + 1) / 2
我们考虑这种情况在求右边界时 右边界恰好等于 l + 1 的情况此时mid 如果等于(r + l)/2 则带入 r = l +1则有 mid = (l + l + 1) / 2 = l 此时q[mid] <= k 成立将mid值赋给l
我们发现在一次二分后我们的区间还是[l,r] 并没有发生改变

但是我们+1后 mid = (l + l + 1 + 1) / 2 = l + 1 此时 mid指向的值恰好为右边界满足q[mid] <= k 条件将此时 l = mid = l + 1 = r 区间更新为 [r, r]就没有问题

代码实现

# include<iostream>
using namespace std;

const int N = 100010;
int q[N];
int n, m;

int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 0; i < n; i++)
	{
		scanf("%d", &q[i]);
	}
	while (m--)
	{
		int k = 0;
		scanf("%d", &k);
		int l = 0, r = n - 1;
		while (l < r)
		{
			int mid = l + r >> 1;//求mid
			if (q[mid] >= k)//找左边界
				r = mid;
			else
				l = mid + 1;
		}
		if (q[l] != k)//找不到左边界 说明没有这个数据 返回 -1
			printf("-1 -1\n");
		else
		{
			printf("%d ", l);//输出左边界
			int l = 0, r = n - 1;
			while (l < r)//找右边界
			{
				int mid = l + r + 1 >> 1;
				if (q[mid] <= k)
					l = mid;
				else
					r = mid - 1;
			}
			printf("%d\n", l);//输出右边界
		}
	}

	return 0;
}