1：单标签二分类：N是样本数，Yn是标签。范围在**[0,1]**。
公式：

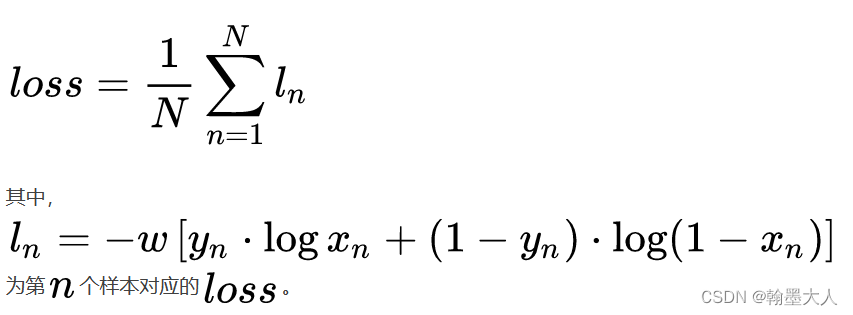
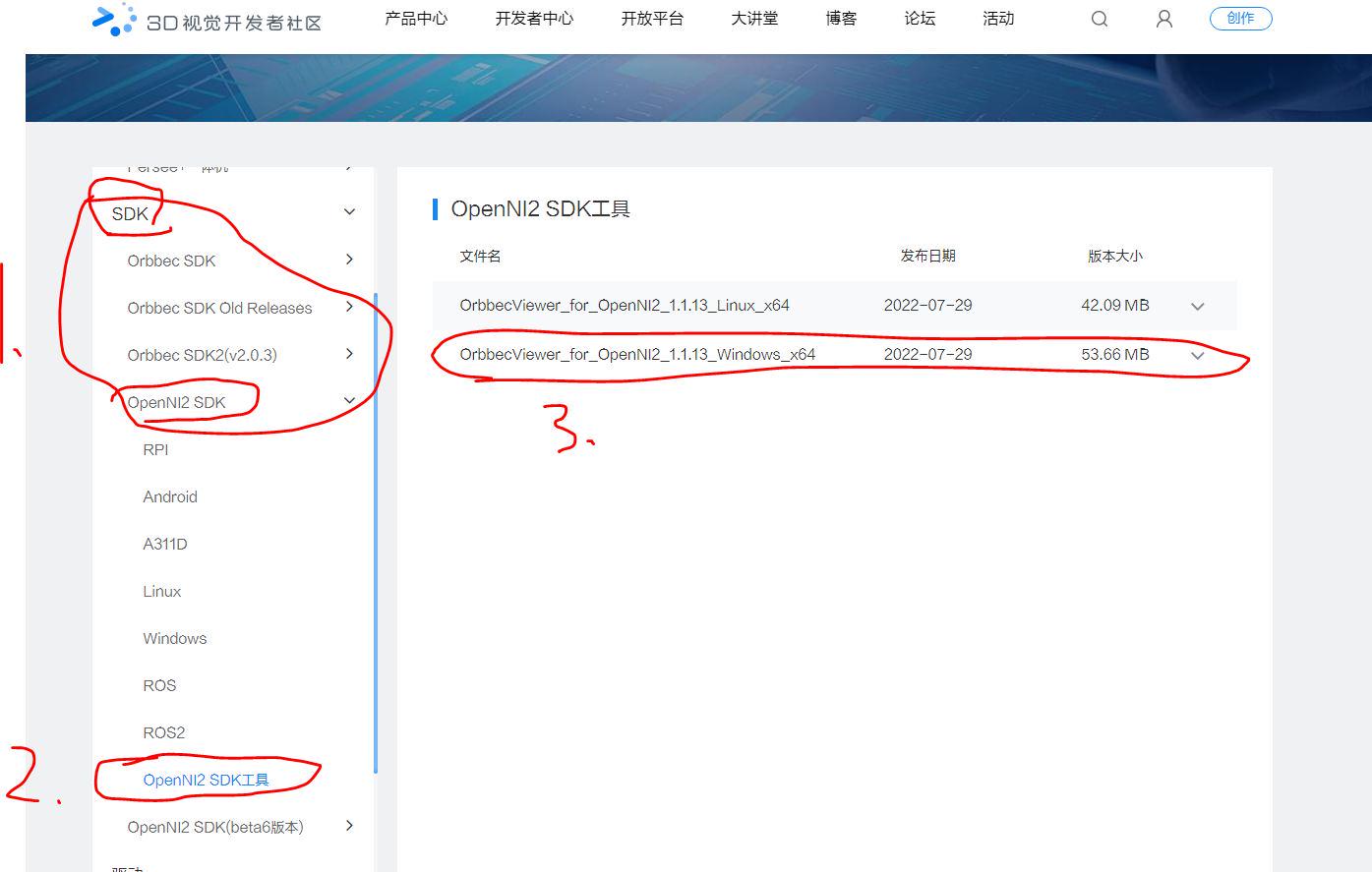
举个例子：

input = torch.Tensor([[0.8, 0.9, 0.3]])#, [0.8, 0.9, 0.3], [0.8, 0.9, 0.3], [0.8, 0.9, 0.3]])
target = torch.Tensor([[1, 1, 0]])#, [1, 1, 0], [1, 1, 0], [1, 1, 0]])
print(input.size())
print(target.size())
output = torch.sigmoid(input)
loss = F.binary_cross_entropy(input, target, reduction='mean')
print(loss)

input是三个样本，对应三个标签。
根据公式可以计算为：-1/3[(1xlog(sigmoid(0.8))+1xlog(sigmoid(0.9))+(1-0)x(log(1-(sigmoid(0.3)))
2:对于多标签的二分类。
计算公式：

input = torch.Tensor([[0.8, 0.9, 0.3], [0.8, 0.9, 0.3], [0.8, 0.9, 0.3], [0.8, 0.9, 0.3]])
target = torch.Tensor([[1, 1, 0], [1, 1, 0], [1, 1, 0], [1, 1, 0]])
print(input.size())
print(target.size())
output = torch.sigmoid(input)
print(output)
loss = F.binary_cross_entropy(output, target, reduction='mean')
print(loss)

首先要明白是几个样本，每个样本有几个标签。
答：有四个样本，非九个样本，每个样本三个标签，非0,1两个标签，看size也能看出来。
首先计算每个样本里面三个数据的损失：

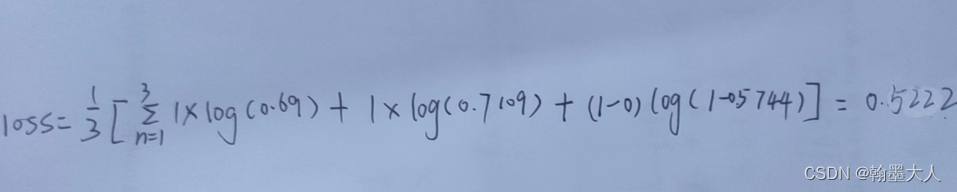
第二第三个第四个同理。
总共损失就等于(0.522*4(每个样本数一样))/4(样本数)=0.522。