这两天看了一下LADRC的。学习深度不够，从理论和原理，没法评论什么。从个人感受上，它会从另一种角度去解释一些的控制的东西。从工程使用上，还是很有参考价值的，参数意义比较明确，整定参数比较容易。

参考：

1. 古典控制与低阶LADRC参数整定(https://www.bilibili.com/video/BV1UD4y117yB/?spm_id_from=333.999.0.0&vd_source=1f88f15c4a8c95c1d720fa4c6218bc54)
2. https://zhuanlan.zhihu.com/p/585324684

---

一阶LADRC

一阶被控对象
$$\dot{y}=b_{0}u+f$$

扩张state-space：
$$\{\begin{array}{l}{\dot{x}}_1=x_2+b_{0}u\\ {\dot{x}}_2=\dot{f}\\ y=x_1\end{array}$$

LESO:
$$\{\begin{array}{l}{\dot{z}}_1={\beta }_1(y-z_1)+z_2+b_{0}u\\ {\dot{z}}_2={\beta }_2(y-z_1)\end{array}$$
控制器：
$$u=\frac{1}{b_0}[l_1(ref-z_1)-z_2]$$

其中
$$l_1={\omega }_c,{\beta }_1=2{\omega }_o,{\beta }_2={\omega }_o^2$$

${\omega }_c$是控制器带宽，${\omega }_o$是观测器带宽。一般选取${\omega }_o=2-10{\omega }_c$。$b_0$跟系统的一些参数有关。

其框图结构：

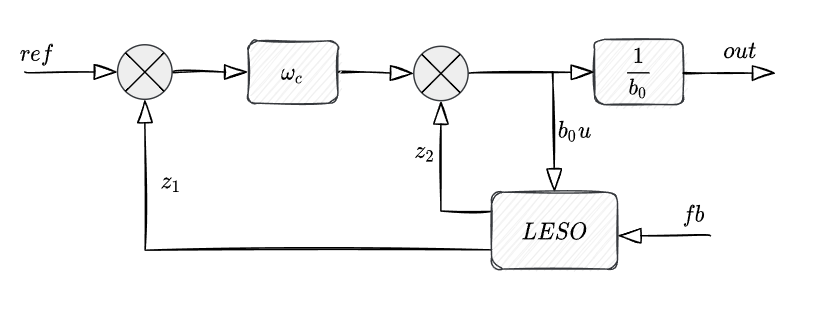
代码实现：

代码实现也很简单，计算量很小。放mcu上，再简单优化一下，也就只比PI多几个乘法和加法。
hpp：

/**
 * @copyright   Copyright wangchongwei 
 * @license:    GNU GPLv2
 * @brief:      adrc 1st
 * @date        2023.03.05
 * @changelog:
 * date         author          notes
 * 2023.03.05   wangchongwei    create file 
 **/

#ifndef  _LADRC_1ST_H_
#define  _LADRC_1ST_H_

class LADRC_1st
{
public:
    LADRC_1st(/* args */);
    ~LADRC_1st();
    void setCtrlParm(double wc, double wo, double b0,double ts);
    void setClampParm(double out_up, double out_low);
    void reset(void);
    double ladrc_1st(double ref,double fb);
private:
    double ts;
    double wc;
    double wo;
    double b0;
    double out_up;
    double out_low;
    double out;

    // observer
    double z[2];
    double dz[2];
};

#endif

cpp:

void LADRC_1st::setCtrlParm(double wc, double wo, double b0,double ts)
{
    this->b0 = b0;
    this->wc = wc;
    this->wo = wo;
    this->ts = ts;
}
void LADRC_1st::setClampParm(double out_up, double out_low)
{
    this->out_up = out_up;
    this->out_low = out_low;
}

double LADRC_1st::ladrc_1st(double ref,double fb)
{
    // leso
    dz[0] = 2*wo*(fb-z[0])+z[1]+b0*out;
    dz[1] = wo*wo*(fb-z[0]);

    z[0] += ts*dz[0];
    z[1] += ts*dz[1];

    // controller
    out = (wc*(ref-z[0])-z[1])/b0;

    if (out > out_up) out = out_up;
    if (out < out_low) out = out_low;

    return  out;
}

github地址：
https://github.com/chongweiwang/CtrlSim/tree/main/lib/controller/adrc