初等变换法求逆矩阵

vba内置函数MInverse可以计算矩阵的逆矩阵，《Office VBA 参考-WorksheetFunction.MInverse 方法 (Excel)》

初等变换法代码思路
对于一个3x3矩阵（下图3x3红色部分）右侧扩充单位矩阵（下图3x3黑色部分），abc为行号

从左往右依次将1-3列非左对角线部分的数值消为0：下图“第1次”将第1列消为0、“第2次”将第2列消为0、“第3次”将第3列消为0。每次计算将固定不变的行值x系数-本行原值=本行现值
系数的计算方法：第n列消0、得到第m行时，系数=(n,m)/(n,n)。取上一次的数组值
如“第1次”，n = 1、m = 2时，系数 = 1/1 = 1；n = 1、m = 3时，系数 = -1/1 = -1
如“第2次”，n = 2、m = 1时，系数 = -4/1 = -4；n = 2、m = 3时，系数 = -2/1 = -2

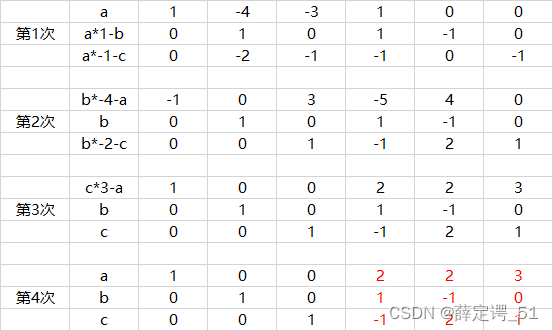
然后检查1-3列左对角线部分的值是否为1，不为1的转为1，对应第4次
值不为1的，整行除该值本身
最后得到左侧为单位矩阵（上图第4次3x3黑色部分）右侧为逆矩阵（上图第4次3x3红色部分），输出右侧逆矩阵即可

Function inverse_matrix(ByVal arr)
    '初等变换法，返回数组矩阵的逆矩阵；arr数组矩阵必须为正方形数值数组
    Dim m&, i&, j&, c&, done As Boolean, coef#
    arr = WorksheetFunction.Transpose(WorksheetFunction.Transpose(arr))  '转为从1开始计数
    If UBound(arr) - LBound(arr) <> UBound(arr, 2) - LBound(arr, 2) Then Debug.Print "非正方形数组": Exit Function
    m = UBound(arr) - LBound(arr) + 1: ReDim mrr(1 To m, 1 To m * 2): ReDim result(1 To m, 1 To m)
    For i = 1 To m
        For j = 1 To m * 2
            If j <= m Then
                mrr(i, j) = arr(i, j)
            Else
                If j - m = i Then mrr(i, j) = 1 Else mrr(i, j) = 0  '扩充单位矩阵
            End If
        Next
    Next
    '将1-m列的非左对角线的值消为0
    Do
        done = True
        For j = 1 To m  '列遍历
            For i = 1 To m  '行遍历
                If j <> i And mrr(i, j) <> 0 Then  '非左对角线，非0
                    done = False: coef = mrr(i, j) / mrr(j, j)  '系数
                    For c = 1 To m * 2
                        mrr(i, c) = mrr(j, c) * coef - mrr(i, c)
                    Next
                End If
            Next
        Next
    Loop Until done = True
    '将1-m列的左对角线的值转为1
    Do
        done = True
        For j = 1 To m  '列遍历
            If mrr(j, j) <> 1 Then
                done = False: coef = 1 / mrr(j, j)  '系数
                For c = 1 To m * 2
                    mrr(j, c) = mrr(j, c) * coef
                Next
            End If
        Next
    Loop Until done = True
    For i = 1 To m    '返回结果数组
        For j = 1 To m
            result(i, j) = mrr(i, j + m)
        Next
    Next
    inverse_matrix = result
End Function

举例

Sub 逆矩阵测试()
    aa = Array(1, 5, 9, 13)
    For Each a In aa
        arr = Cells(a, 1).Resize(3, 3)
        brr = inverse_matrix(arr)
        Cells(a, "e").Resize(3, 3) = brr
        crr = WorksheetFunction.MInverse(arr)
        Cells(a, "i").Resize(3, 3) = crr
    Next
End Sub

计算结果与内置函数MInverse基本一致

矩阵解线性方程组

对于多元一次的线性方程组，利用矩阵求解较为方便
如，方程组

x + y = 8
2x + 4y = 10

矩阵形式

可以用过逆矩阵求得x、y的值

Sub 矩阵解线性方程组()
    'MMult矩阵乘积函数；MInverse矩阵的逆矩阵函数（参数必须为正方形数值数组）
    '矩阵解多元一次方程组，矩阵A*B=C，此处为已知AC求B，B=A逆*C
    arr = [{1, 1; 2, 4}]
    brr = [{8; 10}]
    crr = WorksheetFunction.MMult(WorksheetFunction.MInverse(arr), brr)
    For Each c In crr
        Debug.Print c
    Next
End Sub

结果为11、-3
同理，方程组

x+2y+3z=14
x-y+4z=11
2x+3y-z=5

arr = [{1, 2, 3; 1, -1, 4; 2, 3, -1}]
brr = [{14; 11; 5}]

结果为1、2、3

参考资料
《B站-求逆矩阵的三种方法》
《知乎-矩阵为什么能解方程？》