1. 什么是二叉搜索树

1.若它的左子树不为空，那么左子树上所有节点都小于根节点
2.若它的右子树不为空，那么右子树上所有节点都小于根节点
3.它的左右子树也分别是二叉搜索树
4.使用中序遍历结果是从小到大

---

定义节点，使用静态内部类

static class TreeNode{
        public int val;
        public TreeNode left;
        public TreeNode right;
        public TreeNode(int val) {
            this.val = val;
        }
    }
    public TreeNode root;//根节点

2. 查找二叉搜索树是否有值为key的节点

遍历二叉搜索树，如果节点的值比key小，就往右边走，反之就往左边走

public TreeNode search(int key) {
        if(root == null) {
            return null;
        }
        TreeNode cur = root;
        while(cur != null) {
            if(cur.val == key) {
                return cur;
            }else if(key > cur.val) {
                cur = cur.right;
            }else {
                cur = cur.left;
            }
        }
        return null;
    }

3. 二叉搜索树的插入

在二叉树中插入的新节点都是在叶子上，并且不能插入相同数据的节点

从根节点开始比较，如果比该节点大就往右边走，反之往左边走，直到走到叶子节点。

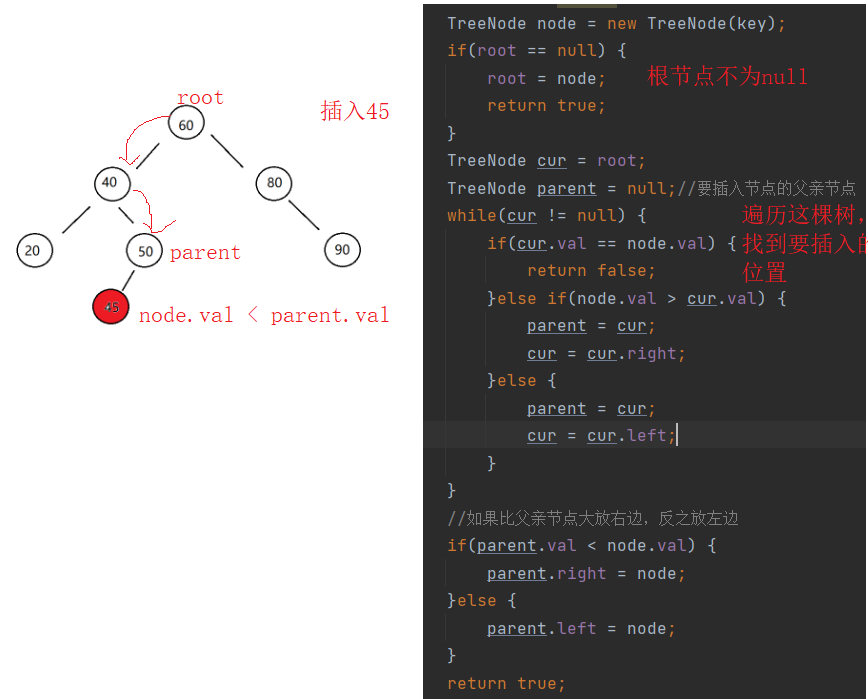
public boolean insert(int key) {
        TreeNode node = new TreeNode(key);
        if(root == null) {
            root = node;
            return true;
        }
        TreeNode cur = root;
        TreeNode parent = null;//要插入节点的父亲节点
        while(cur != null) {
            if(cur.val == node.val) {
                return false;
            }else if(node.val > cur.val) {
                parent = cur;
                cur = cur.right;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //如果比父亲节点大放右边，反之放左边
        if(parent.val < node.val) {
            parent.right = node;
        }else {
            parent.left = node;
        }
        return true;
    }

4. 二叉搜索树的删除（难点）

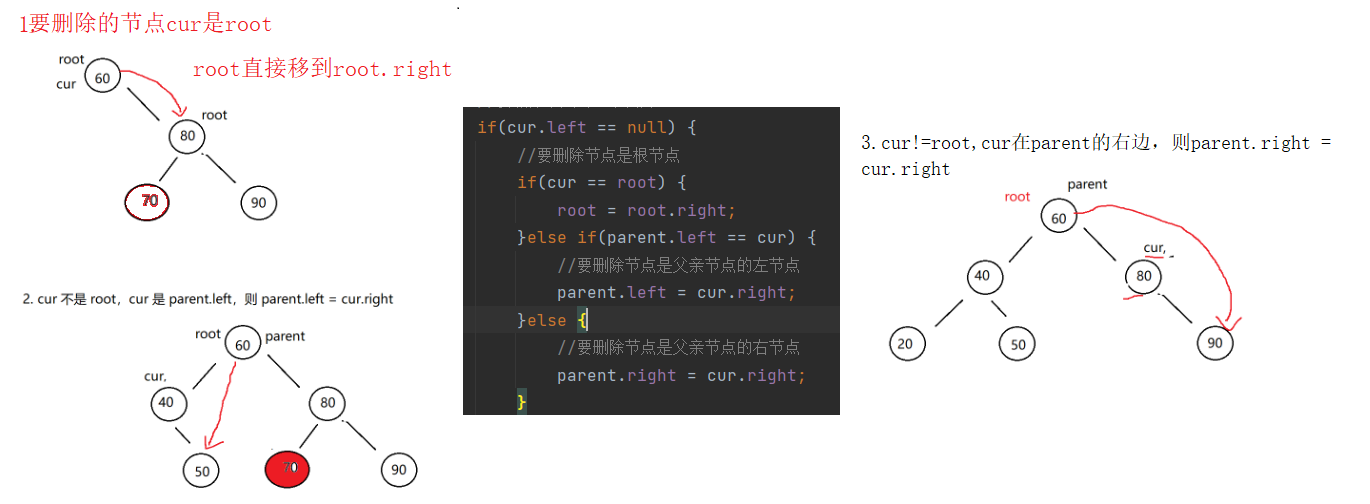
设待删除结点为 cur, 待删除结点的双亲结点为 parent
1. cur.left == null
（1） cur 是 root，则 root = cur.right
（ 2）cur 不是 root，cur 是 parent.left，则 parent.left = cur.right
（ 3） cur 不是 root，cur 是 parent.right，则 parent.right = cur.right
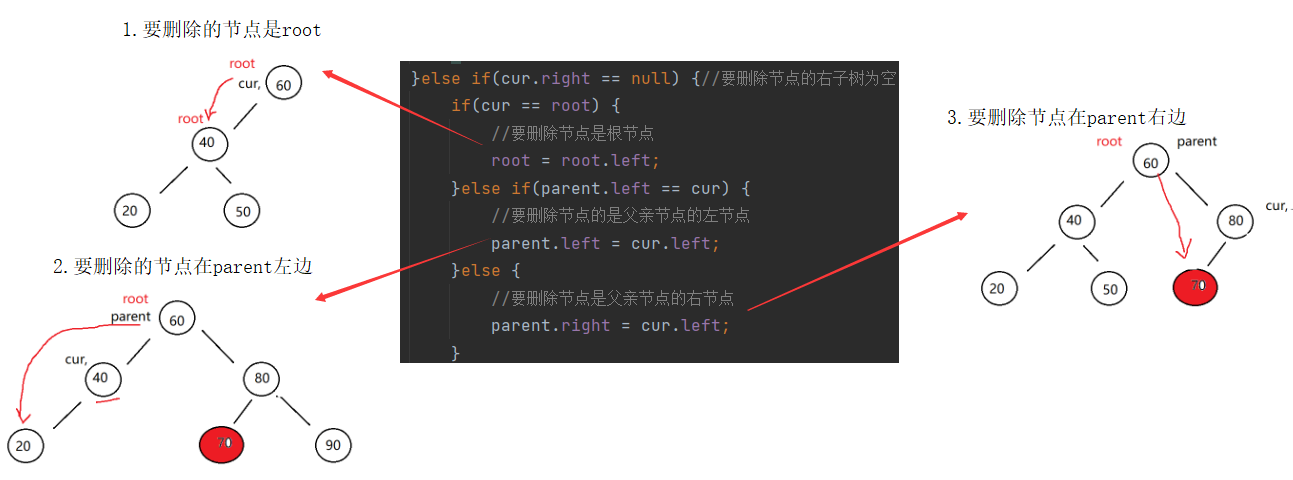
2. cur.right == null
（1） cur 是 root，则 root = cur.left
（ 2） cur 不是 root，cur 是 parent.left，则 parent.left = cur.left
（ 3） cur 不是 root，cur 是 parent.right，则 parent.right = cur.left
3. cur.left != null && cur.right != null
需要使用替换法进行删除，即在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值填补到被删除节点中，再来处理该结点的删除问题

---

我结合画图和代码7个条件一个一个分析过去，别担心

1. 在cur.left==null的前提下

2. 在cur.right == null的前提下

3. cur.left != null && cur.right != null

有两种选择，任选一种。1.去要删除节点cur的左子树找最大值的节点覆盖cur,因为是最大的节点，所以该节点没有右子树，也就是把它当作前面第二种情况来做。
2.去cur的右子树中找最小值的节点覆盖cur，因为是cur右子树的最小节点，所以该节点一定没有左子树，可以把它当作第一种情况来做

---

我的代码是选择第二个

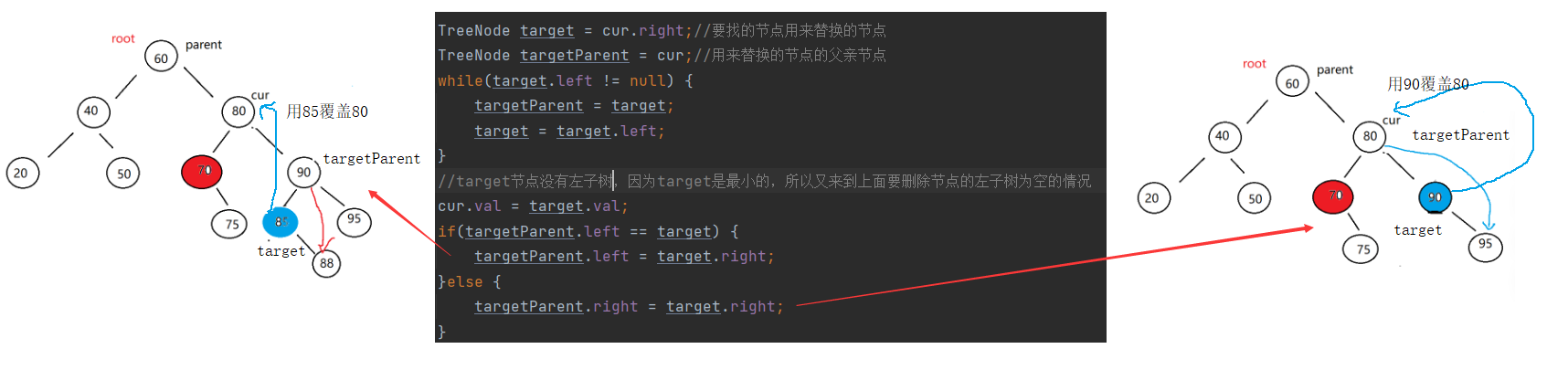
删除的所有代码如下

/**
     * 删除值为key的节点
     * @param key
     */
    public void remove(int key) {
        if(root == null) {
            return;
        }
        TreeNode cur = root;
        TreeNode parent = null;//要删除节点的父亲节点
        while(cur != null) {
            if(key > cur.val) {
                parent = cur;
                cur = cur.right;
            }else if(key < cur.val) {
                parent = cur;
                cur = cur.left;
            }else {
                //找到了
                removeNode(cur, parent);
                return;
            }
        }
    }

    /**
     * 删除节点
     * @param cur 要删除的节点
     * @param parent 要删除的父亲节点
     */
    private void removeNode(TreeNode cur, TreeNode parent) {
        //要删除节点的左子树为空
        if(cur.left == null) {
            //要删除节点是根节点
            if(cur == root) {
                root = root.right;
            }else if(parent.left == cur) {
                //要删除节点是父亲节点的左节点
                parent.left = cur.right;
            }else {
                //要删除节点是父亲节点的右节点
                parent.right = cur.right;
            }
        }else if(cur.right == null) {//要删除节点的右子树为空
            if(cur == root) {
                //要删除节点是根节点
                root = root.left;
            }else if(parent.left == cur) {
                //要删除节点的是父亲节点的左节点
                parent.left = cur.left;
            }else {
                //要删除节点是父亲节点的右节点
                parent.right = cur.left;
            }
        }else {
            //要删除节点的左右子树都不为空
            //使用替换删除的方式进行删除
            //要么在要删除节点的左子树中找到最大值，该节点的右子树一定为空，用它替换cur,
            //要么在要删除节点的右子树中找到最小值，该节点的左子树一定为空，用它替换cur
            //1.找到要替换的节点，采用找右子树的最小值进行替换
            TreeNode target = cur.right;//要找的节点用来替换的节点
            TreeNode targetParent = cur;//用来替换的节点的父亲节点
            while(target.left != null) {
                targetParent = target;
                target = target.left;
            }
            //target节点没有左子树，因为target是最小的，所以又来到上面要删除节点的左子树为空的情况
            cur.val = target.val;
            if(targetParent.left == target) {
                targetParent.left = target.right;
            }else {
                targetParent.right = target.right;
            }
        }
    }

5. 性能分析

无论是插入还是删除都要进行查找，也就是说查找效率越高二叉搜索树的性能就越高。而二叉树搜索树是满二叉树的情况下，树的高度低，时间复杂度O（log2N).极端条件下，二叉搜索树编程单支树就是O（n).所以为了避免这种不平衡的情况，前辈们做了升级变成AVL树就是一棵高度平衡的二叉搜索树，最大高度差只有1.但是为了保证高度差为1付出的代价太大，又引入了红黑树,.