DDIM中遇到的Score-based SDE
这里采用表示神经网络的预测值,用
表示
。同时
等价于

DDPM回顾
贝叶斯公式
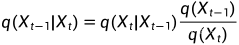
原始公式
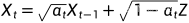
前向过程
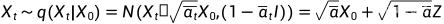
 表示连乘
表示连乘
反向过程

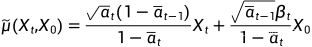
由前向过程可知: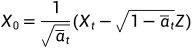
所以: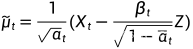
正态分布: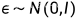
重参数技巧:
反向过程: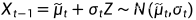
优化目标:
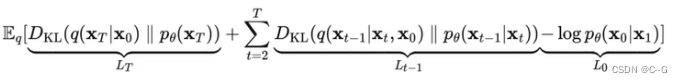
对于两个单一变量的高斯分布 p 和 q而言,KL散度为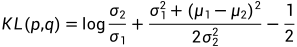
最终简化为: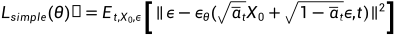
经验贝叶斯估计
根据经验贝叶斯估计,对于应该高斯变量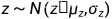 ,有以下结论:
,有以下结论:
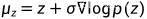
将上式代入前向过程可得
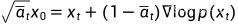
前向过程展开后为: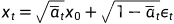 ,对
,对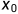 做等价变换
做等价变换
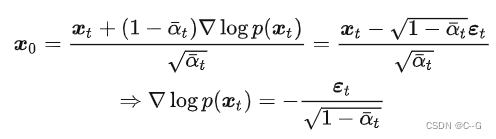
同样的,在DDPM中推导优化目标的时候,是需要先建模出 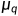 ,然后再用一个神经网络来学习近似它,当时推导的结论是:
,然后再用一个神经网络来学习近似它,当时推导的结论是:
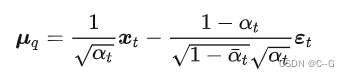
替换 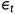 即可以得到一个新的建模方式
即可以得到一个新的建模方式
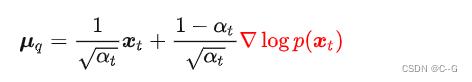
将逆向估计过程建模成
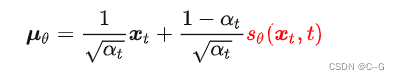
重新推导DDPM中的优化目标
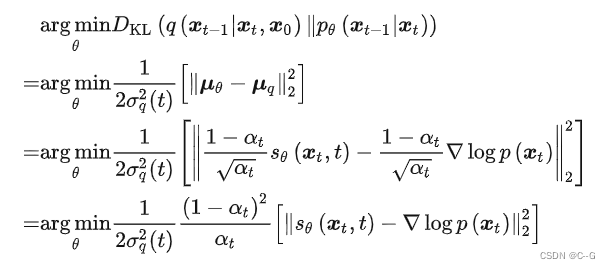
其中 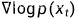 称为 score function
称为 score function
Score Matching
回到数据分布p(x) 的估计问题上来,任意一个概率分布,可以用一个更加通用的形式来表示:
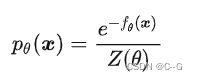
这来源于能量模型 (Energy-Based Models)。 代表一个归一化常数,来确保p.d.f积分
代表一个归一化常数,来确保p.d.f积分 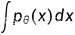 等于1。通常的估计方法是最大似然估(MLE),但就不得不去先考虑分母,因为它是不知道的。如何消除这个归一化项z(θ)的影响?就有如下几类:
等于1。通常的估计方法是最大似然估(MLE),但就不得不去先考虑分母,因为它是不知道的。如何消除这个归一化项z(θ)的影响?就有如下几类:
Flow 限制 Z=1。
VAE|GAN 没有消除Z,直接硬去用一些Measure测度方法估计,VAE找到一个距离的证据下界,GAN直接用网络去学距离度量。
Score-based 直接消掉Z,对p求对数梯度
这里讨论第三种方法
对 求对数梯度
求对数梯度

而优化过程可以直接用一个神经网络 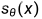 来近似,从真实数据 p(x) 中采样一个变量,然后求对数梯度,就提供了一个优化方向:
来近似,从真实数据 p(x) 中采样一个变量,然后求对数梯度,就提供了一个优化方向:
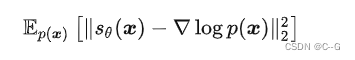
数据空间的每个点都被赋予了一个分数向量 (score vector),从初始点开始不断迭代,最终能到达目标数据所在的区域。
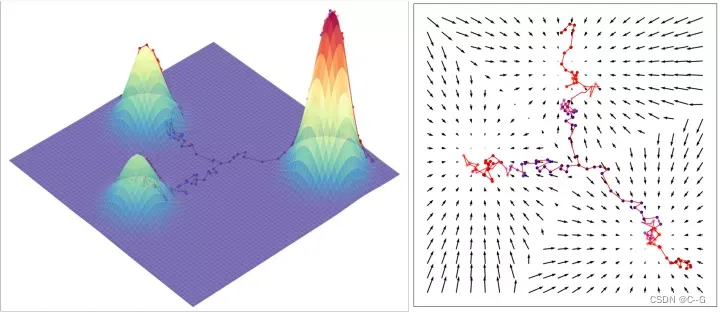
这里结果都出来了,还不知道怎样一步一步迭代更新的呢?
这里其实也是要说明为什么这个score function那么重要,我们那么关心?
是因为一旦知道了这个score(p(x)对输入x的梯度),就可以使用朗之万动力学(Langevin dynamics)采样数据,过程是

其中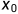 是随机初始点;
是随机初始点;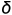 是一个比例系数;
是一个比例系数;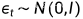 是一个扰动项,避免采样结果崩塌到一个固定点。当
是一个扰动项,避免采样结果崩塌到一个固定点。当 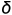 足够小,T 足够大的时候,最终的
足够小,T 足够大的时候,最终的  就是真实数据。
就是真实数据。
Score Matching优化方向可以转换为:
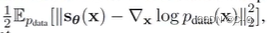
原论文公式
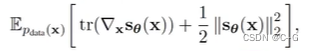
转换后公式
这里复杂的雅可比矩阵运算很麻烦,可以通过denoising score matching | sliced score matching 绕过这个运算
Denoising score matching 首先对数据样本加预先定义的噪声分布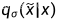 ,同样用分数匹配的方法估计加噪后数据的分数
,同样用分数匹配的方法估计加噪后数据的分数
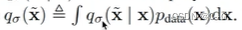
对加噪后数据使用Score Matching
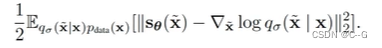
训练收敛后,可以认为 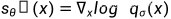 ,但是只有当加的噪声非常小的时候才成立。
,但是只有当加的噪声非常小的时候才成立。
Noise Conditional Score Networks(NVSN)
还有一个问题,低密度区域的样本太少,估计就会不准确,甚至某些采样点的概率可能为0,那么取对数就没有意义了,也就是说训练效果会不好。
这里可以加入高斯噪声,就减少了零概率的出现,使得低密度区域也有了更多的样本
如何确定噪声的大小就成了问题的关键,目前提出的是加一系列不同尺度的噪声,然后分步训练每一尺度的score matching网络,具体过程是先引入一系列噪声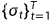 ,然后就可以得到对应的噪声扰动后的分布:
,然后就可以得到对应的噪声扰动后的分布:
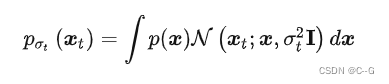
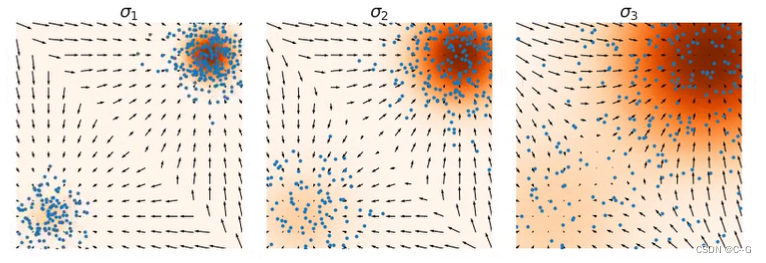
用一个原图来帮助理解,要训练的是图中的箭头 (大小和方向),随着 增大,学到的箭头越来越细腻。
增大,学到的箭头越来越细腻。
目标函数可以改写为:
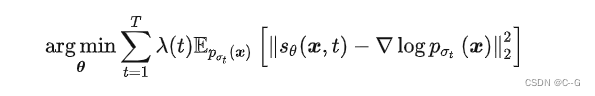
其中 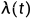 是一个关于 t 的权重向量,也就是实现了前面说的分不同噪声尺度训练。在这种设定下,朗之万动力学采样也是分尺度来做,只不过是逆着来,从 t = T 到 t = T−1,最后到 t=1。直觉上高噪声提供了低密度区域较好的引导,低噪声提供了高密度区域较好的引导,这样使得整个采样过程更加稳定。
是一个关于 t 的权重向量,也就是实现了前面说的分不同噪声尺度训练。在这种设定下,朗之万动力学采样也是分尺度来做,只不过是逆着来,从 t = T 到 t = T−1,最后到 t=1。直觉上高噪声提供了低密度区域较好的引导,低噪声提供了高密度区域较好的引导,这样使得整个采样过程更加稳定。
Learning NCSN via score matching
定义的噪声分布可以表示为:
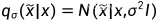
因此,原始数据的分数函数表示为:
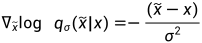
对于给定 σ 的噪声分数匹配目标函数为
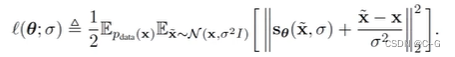
结合NCSN,对于所有噪声 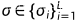 ,目标函数变换为:
,目标函数变换为:
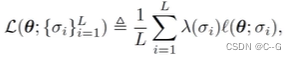
使用发现 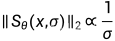 ,因此选择
,因此选择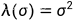 ,在这种情况下有:
,在这种情况下有:
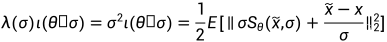
又因为 ,
,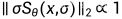 ,所以
,所以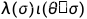 不依赖于 σ
不依赖于 σ
NCSN inference via annealed Langevin dynamics

生成噪声序列,从大到小,
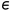 很小的值,T Langevin 迭代次数,随机生成一个
很小的值,T Langevin 迭代次数,随机生成一个
循环噪声序列,与噪声相关的步长
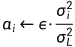 ,由于噪声序列由大到小,步长由大到小
,由于噪声序列由大到小,步长由大到小
T 步Langevin 采样
Langevin 迭代后的
 作为下一次采样的初始值
作为下一次采样的初始值 
分数估计和 Langevin dynamics 在高密度区域表现较好,所以高密度区域的样本可以作为下一次Langevin 采样的初始值
σ 设置为等比数列比较好
参数更新时加上EMA更稳定
实验中,设置 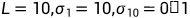
SDE
如果把上述有限步 T 拓展到无限步会怎么样?因为经过实验验证, T 越大,可以得到更准确的似然估计,以及质量更好的结果。而这样对数据进行连续时间的扰动就可以被建模成一个随机微分方程 (stochastic differential equation, SDE)。

SDE的形式有很多种,宋飏博士在论文中给出的一种形式 (可以算作是Diffusion-Type SDE,要求系数只与时间t和当前时刻取值 x 有关) 是:
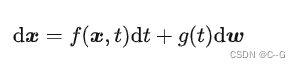
其中 f(⋅) 被称为 漂移系数 (drift coefficient),g(t) 被称为 扩散系数 (diffusion coefficient),w 是一个标准的布朗运动,dw 就可以被看成是一个白噪声。这个随机微分方程的解就是一组连续的随机变量 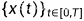 ,这里 t 就是把上面的离散形式 (1,2,…,T) 连续化,同时用
,这里 t 就是把上面的离散形式 (1,2,…,T) 连续化,同时用  表示 x(t) 的概率密度函数,这也和前面的
表示 x(t) 的概率密度函数,这也和前面的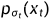 能对应上,
能对应上, 是原数据分布,
是原数据分布,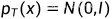 是加噪声扰动到最后变成了白噪声。
是加噪声扰动到最后变成了白噪声。
Reverse SDE的逆向过程依旧是一个SDE,表达式为:
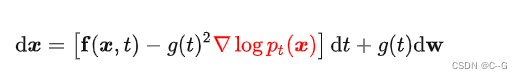

看DDPM和SDE的联系,上面提及前向过程的传递公式 (这里得用 β 的形式,同时为了和下面公式中的 t 区分,这里改写为下标 i ):
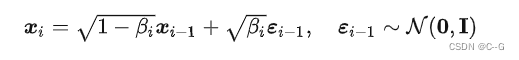
这是一个离散过程,如何连续化一下得到SDE呢? 到
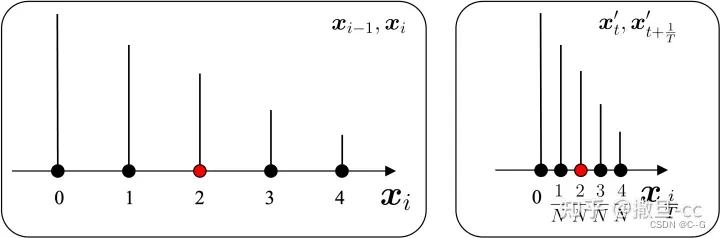
到  是稀疏相邻的两个变量过程,可以让稀疏的分布变稠密一点,对变量索引除以 T ( T 趋向于无穷大),这样变量索引就从 i∈{0,1,…,T} 变成了
是稀疏相邻的两个变量过程,可以让稀疏的分布变稠密一点,对变量索引除以 T ( T 趋向于无穷大),这样变量索引就从 i∈{0,1,…,T} 变成了  ,如下图所示:
,如下图所示:
做一些变换
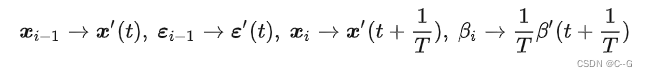
上述变换里,只有最后一个  有一个 N 倍的放缩,这是为了后面能配凑出 Δt 。
有一个 N 倍的放缩,这是为了后面能配凑出 Δt 。
此刻的  ,那么现在就可以改写上述前向过程的传递公式
,那么现在就可以改写上述前向过程的传递公式
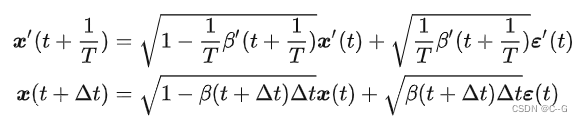
借助一阶泰勒展开的结论 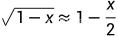 ,上式就可以写成:
,上式就可以写成:
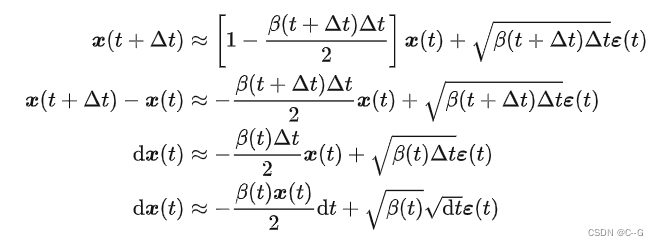
得到类似Diffusion-Type SDE的形式
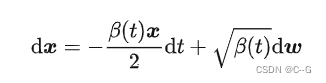
前面离散过程里,采用朗之万动力学采样生成新样本。那这里推导了正向过程的SDE,要想生成样本,需要的是逆向过程,Reverse SDE的逆向过程依旧是一个SDE,表达式为:
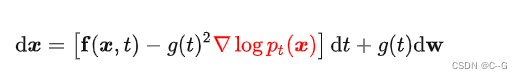
求解上面这个方程就能得到一个 score-based generative model。红色标记部分是不是就是score function,也就是说任务就是要估计这个score function,和前面一致地训练一个网络来近似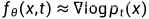
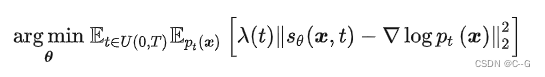
这个目标函数的求解依旧采用前面提及到的“score matching”方法。逆向过程用一个示意图来展示
而关于常微分方程 (ordinary differential equation (ODE)),在原论文中展示了从SDE到ODE的转换,一方面我们可以借助更多的ODE求解器来帮助快速求解 (ODE因为没有随机性,因此可以用更大的步长来求解),同时能计算更准确的对数似然。SDE的逆向过程对应的ODE如下:
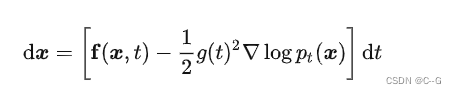
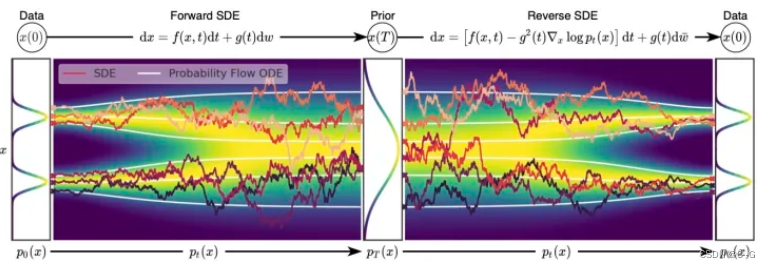
以及展示一个SDE|ODE正向和逆向过程的示意图,ODE是白线表示,显得更加稳定,同时他们俩得到的分布是一样的
从DDPM的角度不好推出条件概率的形式,也就不好表示可控生成 (conditional generation)。从SDE的角度将能很好地解决这个麻烦。借由贝叶斯定理:
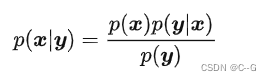
两边同时对 x 求偏导得到
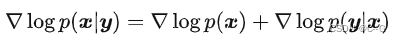
后两项都是可以估计的score function,因此可以通过Langevin-MCMC生成 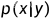
Estimating the reverse SDE with denoising score matching
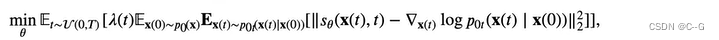
需要训练一个时间相关的 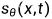 模型去逼近
模型去逼近 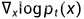
时间 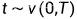 是一个 均匀分布
是一个 均匀分布 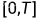 (会做归一化),
(会做归一化),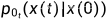 表示从 x(0) 到 x(t) 的转移概率,取决于加噪过程,
表示从 x(0) 到 x(t) 的转移概率,取决于加噪过程,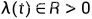 表示正加权函数一般设置为
表示正加权函数一般设置为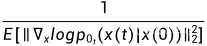 ,如果该分布是高斯分布,则就是方差
,如果该分布是高斯分布,则就是方差
Tips on designing score-based models