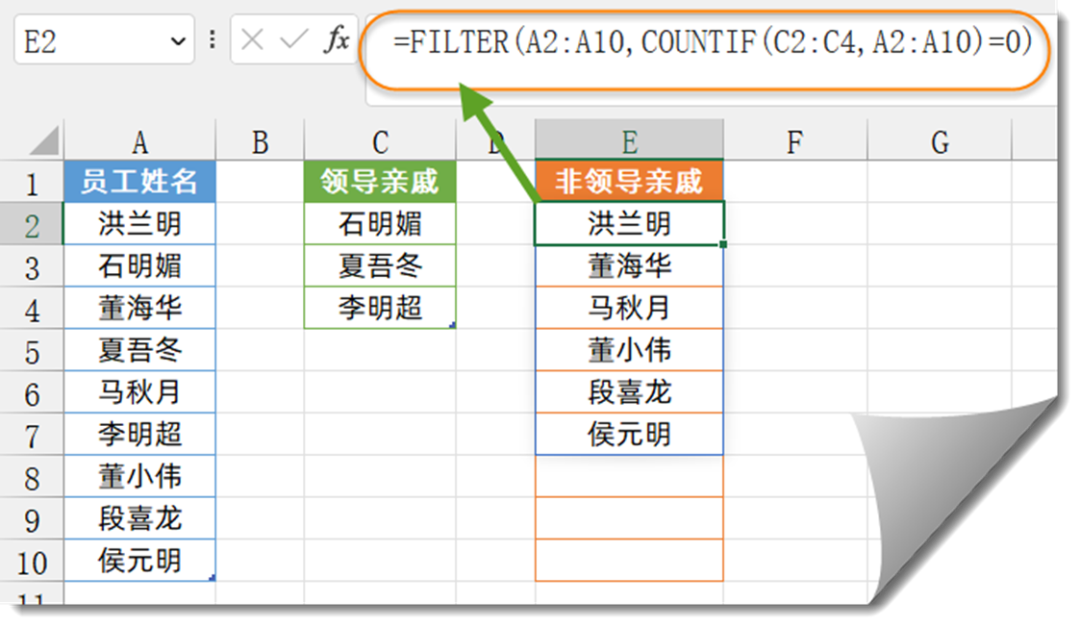
目录

定理：

极限运算法则：

 极限存在之间的计算：

例题：

 定理：

---

定理：

定理1和定理2的证明方式类似，我们对定理2进行证明。

 我们举一个例子：

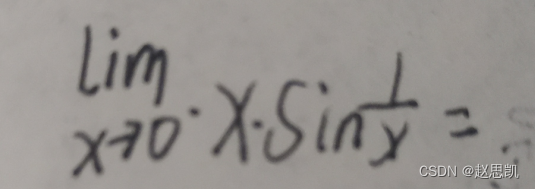
这道题目的结果是0，但是计算方式需要搞清楚。

许多同学是这样计算的：因为第一项x的极限值为0，所以我们不需要计算了，结果为0，这样写对吗？

答： 

 正确的解题方法如下：

两个无穷小的和为无穷小，进而我们可以推出有限的无穷小的和为无穷小。

但是对于无限个无穷小，它的和就不一定了：

 

所以无限个无穷小的和不一定为无穷小。

 

 因为常数就是有界函数，有界函数与无穷小的成绩就是无穷小，所以常数与无穷小的乘积是无穷小。

证明：

 

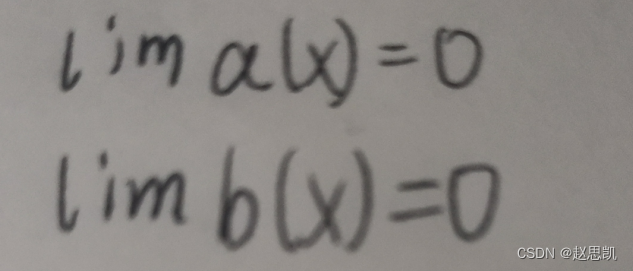
 a(x)的极限是存在的，那么a(x)就是有界函数，有界函数乘以无穷小的结果仍然为无穷小。

极限运算法则：

这些加法乘法的法则只有在极限存在的情况下才可以使用。

我们对乘法运算进行证明：

 极限存在之间的计算：

我们进行证明：

 

 

 

 我们进行证明：

 

我们不再证明/。

 因为我们可以把常数当作极限值来算：

 

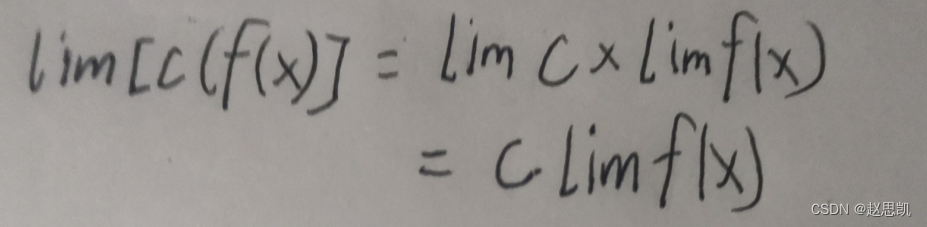
我们可以这样证明：

 

 

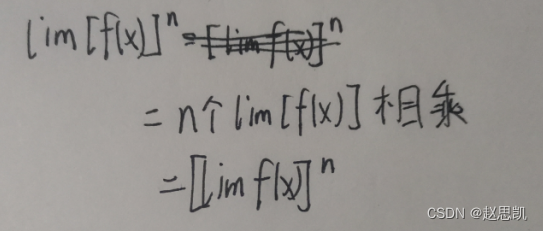
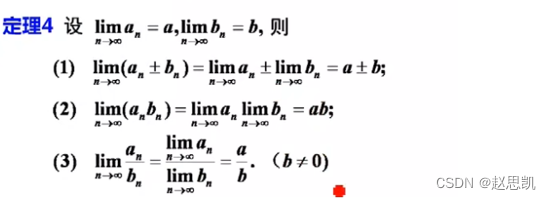
 数列极限和函数极限是一样的。

例题：

 

 

 

 

 

 

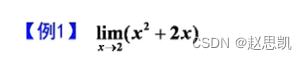
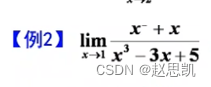
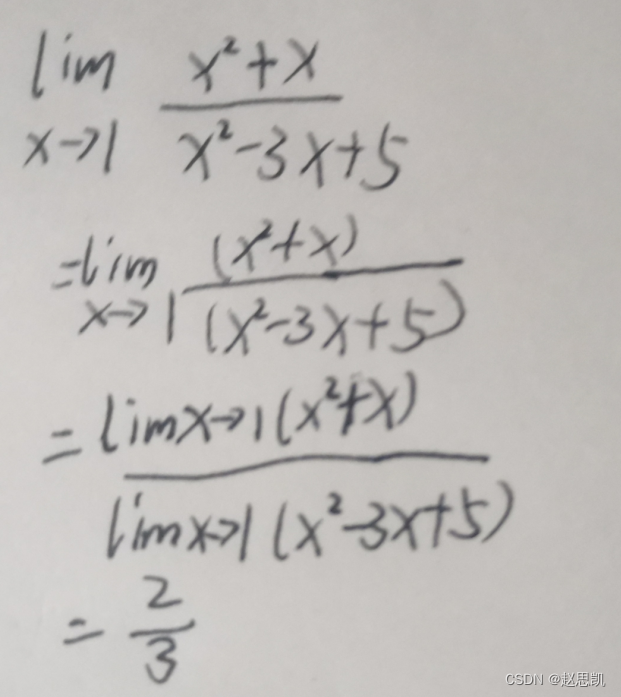
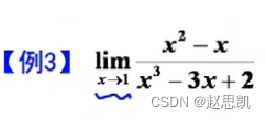
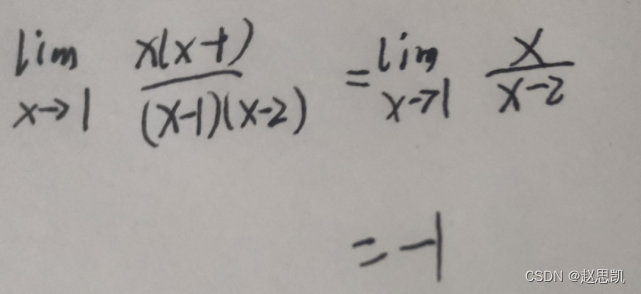
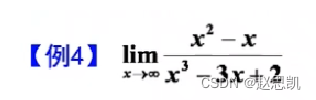
 对于这种多项式，我们可以让分子分母同时除分母最大的次方项

 

 

 

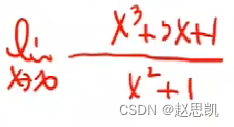
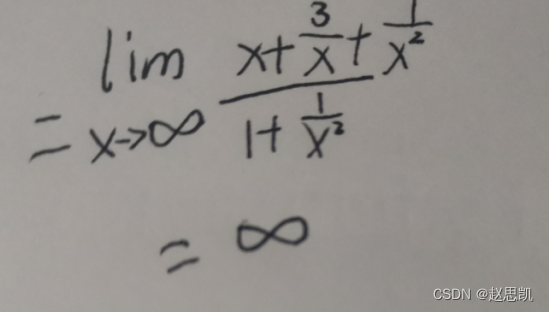
由此，我们可以总结出一个规律。

对于无穷比无穷的类型的多项式：

分子的最高次项大于分母的最高次项时，结果为正无穷。

分子的最高次项等于分母的最高次项时，结果为常数

 分子的最高次项小于分母的最高次项时，就是常数。

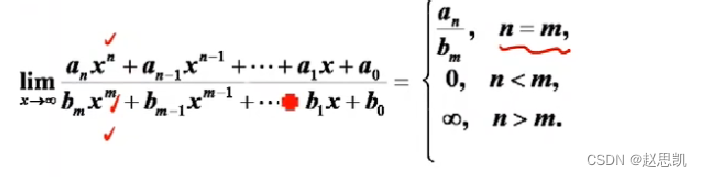
 定理：

 

 

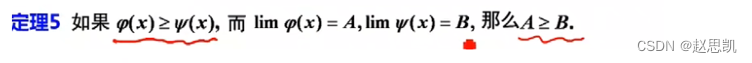
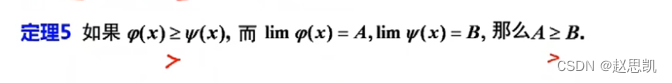
假如我们把这里的大于等于换成大于号会怎么样呢？

答： 我们举一个例子：

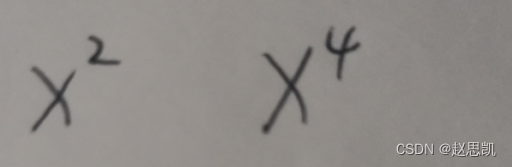
当x大于1时，x的四次方是大于x的平方的，但是x平方和x四次方的极限值都为无穷，并不存在大于等于关系。

 

 为什么这里要加上g(x)不等于u0？

答：例如：

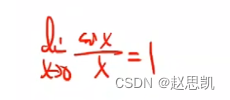
 根据这个极限，我们可以得出这个吗？

 不行，我们只保证了[]趋近于0但是不等于0，但是并没有限制内部的自变量。

假如我们的[]函数是这样呢？

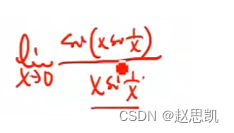
 我们还要保证[]内部的函数不等于0才行。