文章目录
- ALGORITHM
- BASIC INFORMATION
- Basic algorithm design technology
- 穷举法
- 分治法
- 减治法
- 动态规划法
- 贪心法
- Algorithm design technology based on search
- 回溯法
- 分支限界法
- PRACTICE
- CONCEPT
- CALATION*
- CODE
- prim&dijkstra&kruskal
- 分治法
- Q&A
- T ( n ) T(n) T(n) 是渐进时间复杂度
- 算法复杂度渐进符号
- other
https://www.zhihu.com/question/301082100
ALGORITHM
BASIC INFORMATION
-
算法
重要问题类型 查找、排序、图、组合、几何 5个性质 可行性,确定性,有穷性,输入,输出。 算法分析 时间复杂度与问题规模相关 -
算法分析
Basic algorithm design technology
穷举法
-
基本思想
-
In computer science, brute-force search or exhaustive search, also known as generate and test, is a very general problem-solving technique and algorithmic paradigm
-
在计算机科学中,蛮力搜索和穷举搜索,被也称为生成和测试,是已知非常普遍的问题解决方法和算法范式
-
that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem’s statement.
-
该方法由系统的枚举所有可能的候选解决方案和检查每个候选是否码中问题的陈述。
-
-
-
例子
-
问题
- 鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱一,百钱买百鸡,问翁、母、雏各几何?
-
解决方法
import java.util.ArrayList; import java.util.List; public class test { public static void main(String[] args) { int money = 100; List<int[]> ans_list = HundredBuyChick(money); } static public List<int[]> HundredBuyChick(int money){ List<int[]> ans_list = new ArrayList<>(); int[] ans = new int[3]; for (int i = 1; i <= 20; i++) { for (int j = 1; j <= 34; j++) { for (int k = 1; k <= 100; k++) { int current = 5*i+3*j+k; if(current==money){ System.out.println(current+" "+i+" "+j+" "+k); ans[0]=i; ans[1]=j; ans[2]=k; ans_list.add(ans); } } } } return ans_list; } }
-
分治法
-
基本思想
-
recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem.
Recursion solves such recursive problems by using functions that call themselves from within their own code.
-
递归通过使用从自己的代码中调用自身的函数来解决此类递归问题。
-
递归是一种解决计算问题的方法,其中的解决方案取决于同一问题的较小实例的解决方案。
-
In computer science, divide and conquer is an algorithm design paradigm. A divide-and-conquer algorithm recursively breaks down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem.
-
在计算机科学中,分治是一种算法设计范式。
-
分治算法递归地将一个问题分解为两个或多个相同或相关类型的子问题,
-
直到这些子问题变得简单到可以直接解决。
-
然后将子问题的解决方案组合起来以给出原始问题的解决方案。
-
-
例子
-
问题
- 给定有序数组为 a r r a y s arrays arrays,输入一个数 x x x,
- 使用二分查找的方法在给定数组中对其进行查找,若找到返回x的索引,否则返回 − 1 -1 −1。
-
解决方法
import java.util.ArrayList; import java.util.Arrays; import java.util.List; public class test { public static void main(String[] args) { int number = 11; int[] arrays = new int[]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10,99,4,8,7,9,2,4,13,578,5,11}; int numberIndex = binarySearch(number, arrays); } static public int binarySearch(int number, int[] arrays) { Arrays.sort(arrays); int right = arrays.length; int left = 0; while (right >= left) { int mid = left + (right - left) / 2; if (arrays[mid] > number) { right = mid - 1; } else if (arrays[mid] < number) { left = mid + 1; } else{ return mid; } } return -1; } } -
问题
- 给定默认数组 a r r a y s arrays arrays,使用合并排序的方法,将该数组按从小到大的顺序排序并输出。
-
解决方法
public class test { public static void main(String[] args) throws Exception { int number = 11; int[] arrays = new int[]{99, 4, 15, 12, 4, 7, 8}; Solution solution = new Solution(); int[] ans = solution.mergeSort(arrays, 0, arrays.length - 1); } } class Solution { public int[] mergeSort(int[] arrays, int l, int r) throws Exception { // 递归判断条件 if (l < r) { int mid = (l + r) / 2; // 左归并 mergeSort(arrays, l, mid); // 右归并 mergeSort(arrays, mid + 1, r); //合并左右归并 merge(arrays, l, mid, r); } return arrays; } public void merge(int[] arrays, int l, int mid, int r) { int[] temp = new int[r - l + 1]; int i = l; int j = mid + 1; int k = 0; // 左右数组相同长度部分 while (i <= mid && j <= r) { if (arrays[i] < arrays[j]) { temp[k++] = arrays[i++]; } else { temp[k++] = arrays[j++]; } } // 左数组剩余 while (i <= mid) { temp[k++] = arrays[i++]; } // 右数组剩余 while (j <= r) { temp[k++] = arrays[j++]; } // 将temp的值赋给arrays if (temp.length >= 0) System.arraycopy(temp, 0, arrays, l + 0, temp.length); } }-
问题
- 给定默认数组 a r r a y s arrays arrays,使用快速排序的方法,将该数组按从小到大的顺序排序并输出。
-
解决方法
public class test { public static void main(String[] args) throws Exception { int number = 11; int[] arrays = new int[]{4, 99, 15, 12, 1, 7, 8}; Solution solution = new Solution(); solution.quickSort(arrays, 0, arrays.length - 1); System.out.println(arrays); } } class Solution { public void quickSort(int[] arrays, int l, int r) { if (l > r) { return; } int i = l; int j = r; int temp = arrays[l]; while (i < j) { while (temp <= arrays[j] && i < j) { j--; } while (temp >= arrays[i] && i < j) { i++; } if (i < j) { int t = arrays[j]; arrays[j] = arrays[i]; arrays[i] = t; } } arrays[l] = arrays[i]; arrays[i] = temp; quickSort(arrays, l, j - 1); quickSort(arrays, j + 1, r); } }
-
-
问题
-
循环赛日程表,设有 n = 2 k , k ∈ R n=2^k,k \in R n=2k,k∈R个运动员要进行比赛。
-
设计一个满足以下要求的比赛日程表:
-
每个选手必须与其他 n − 1 n-1 n−1个选手各赛一次;
-
每个选手一天只能赛一次;
-
循环赛一共进行 n − 1 n-1 n−1 天。
-
-
-
解决方法
public class test { public static void main(String[] args) throws Exception { int k = 3; int n = (int) Math.pow(2.0, (double) k); int[][] arrays = new int[n + 1][n + 1]; Solution solution = new Solution(); solution.Table(k, arrays); System.out.println(arrays); } } class Solution { public void Table(int k, int[][] arrays) { int n = (int) Math.pow(2.0, (double) k); for (int i = 1; i < arrays.length; i++) { arrays[1][i] = i; } int changeSpan = 1; for (int s = 1; s <= k; s++) { n = n / 2; for (int changeNumber = 1; changeNumber <= n; changeNumber++) { for (int i = changeSpan + 1; i <= 2 * changeSpan; i++) { for (int j = changeSpan + 1; j <= 2 * changeSpan; j++) { arrays[i][j + (changeNumber - 1) * changeSpan * 2] = arrays[i - changeSpan][j + (changeNumber - 1) * changeSpan * 2 - changeSpan]; arrays[i][j + (changeNumber - 1) * changeSpan * 2 - changeSpan] = arrays[i - changeSpan][j + (changeNumber - 1) * changeSpan * 2]; } } } changeSpan = changeSpan * 2; } } }
-
减治法
-
基本思想
-
The reduction-and-conquer method also divides a large problem into several subproblems, but these subproblems do not need to be solved separately, only one of them needs to be solved, so there is no need to merge the solutions of the subproblems. Therefore, strictly speaking, the subtractive method should be a degenerated divide-and-conquer method, and the time complexity is generally O(logn).
减治法同样是把一个大问题划分为若干个子问题,但是这些子问题不需要分别求解,只需求解其中的一个子问题,因而也无需对子问题的解进行合并。 所以,严格的说,减治法应该是一种退化了的分治法,时间复杂性一般是O (logn)。
-
动态规划法
-
基本思想
-
Dynamic programming is both a mathematical optimization method and a computer programming method.
In both contexts it refers to simplifying a complicated problem by breaking it down into simpler sub-problems in a recursive manner.
While some decision problems cannot be taken apart this way, decisions that span several points in time do often break apart recursively.
动态规划既是一种数学优化方法,也是一种计算机编程方法。
在这两种情况下,它都指通过以递归方式将复杂问题分解为更简单的子问题来简化复杂问题。
虽然一些决策问题不能以这种方式分解,但跨越多个时间点的决策往往会递归分解。
-
-
例子
-
问题
- 给定两个字符串 t e x t 1 text1 text1 和 t e x t 2 text2 text2,返回这两个字符串的最长 公共子序列。
- 如果不存在 公共子序列 ,返回
""。
-
解决方法
public class test { public static void main(String[] args) throws Exception { String text1 = "bacaceace"; String text2 = "ace"; String a = text2.substring(0, 2); Solution solution = new Solution(); String ans = solution.longestCommonSubsequence(text1, text2); System.out.println(ans); } } class Solution { public String longestCommonSubsequence(String text1, String text2) { if (text1.equals("") || text2.equals("")) { return ""; } int m = text1.length(); int n = text2.length(); int[][][] dp = new int[m + 1][n + 1][3]; int firstIndex = 0; int secondIndex = 0; for (int i = 1; i <= m; i++) { char text1Char = text1.charAt(i - 1); for (int j = 1; j <= n; j++) { char text2Char = text2.charAt(j - 1); if (text1Char == text2Char) { dp[i][j][0] = dp[i - 1][j - 1][0] + 1; if (dp[i][j][0] == 1) { dp[i][j][1] = j - 1; } else { dp[i][j][1] = dp[i - 1][j - 1][1]; } dp[i][j][2] = j; } else { dp[i][j] = dp[i - 1][j][0] > dp[i][j - 1][0] ? dp[i - 1][j] : dp[i][j - 1]; } } } return text2.substring( dp[m][n][1],dp[m][n][2]); } } -
问题
-
0-1背包问题
-
给定 n n n种物品和一背包。物品 i i i的重量是 w i w_i wi,其价值为 v i v_i vi,背包的容量为 c c c。
-
问应如何选择装入背包中的物品,使得装入背包中的物品的总价值最大?
-
-
解决方法
import java.util.Arrays; public class test { public static void main(String[] args) throws Exception { // weight value int[][] bagObject = new int[][]{{1, 2}, {3, 5}, {2, 7}, {4, 1}}; int capacity = 5; Solution solution = new Solution(); int ans = solution.BagProblem(capacity, bagObject); System.out.println(ans); } } class Solution { public int BagProblem(int capacity, int[][] bagObject) { int[][] dp = new int[bagObject.length + 1][capacity + 1]; dp[0][0] = 0; for (int i = 1; i <= bagObject.length; i++) { for (int j = 0; j <= capacity; j++) { if (j >= bagObject[i-1][0]) { dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - bagObject[i-1][0]] + bagObject[i-1][1]); } else { dp[i][j] = dp[i - 1][j]; } } } return dp[bagObject.length][capacity]; } }
-
贪心法
-
基本思想
-
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage.
In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.
-
贪婪算法是任何遵循问题解决启发式的算法,即在每个阶段做出局部最优选择。
-
在许多问题中,贪婪策略并不产生最优解,但贪婪启发式可以在合理的时间内产生接近全局最优解的局部最优解。
-
-
例子
-
问题
- 有 n n n 个活动申请使用同一个礼堂,每项活动有一个开始时间和一个截止时间,
- 如果任何两个活动不能同时举行,问如何选择这些活动,从而使得被安排的活动数达到最多?
-
解决方法
import java.util.Arrays; public class test { public static void main(String[] args) throws Exception { // weight value int[] start = new int[]{1, 3, 5, 6, 7}; int[] end = new int[]{2, 5, 7, 9, 10}; int totalTime = 10; Solution solution = new Solution(); int[] ans = solution.BagProblem(start, end, totalTime); System.out.println(ans); } } class Solution { public int[] BagProblem(int[] start, int[] end, int totalTime) { int[] ans = new int[start.length]; if (start.length > 0) { ans[0] = start[0]; } int currentIndex = 0; for (int i = 1; i < start.length; i++) { if (end[currentIndex] <= start[i]) { ans[i] = start[i]; currentIndex = i; } } return ans; } }
-
Algorithm design technology based on search
回溯法
-
基本思想
- 回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。
- 回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,
- 这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
-
例子
-
问题
- 八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例。
- 该问题是国际西洋棋棋手马克斯·贝瑟尔于 1848 1848 1848年提出:在 8 × 8 8×8 8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,
- 即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
-
解决方法
import java.util.Arrays; import java.util.LinkedList; public class test { public static int count = 0; public static void main(String[] args) throws Exception { int startX = 0; int startY = 0; Solution solution = new Solution(); LinkedList<Location> list = new LinkedList<Location>(); solution.eightQueen(list, startX, startY); System.out.println(count); } } class Solution { public void eightQueen(LinkedList<Location> list, int startX, int startY) { if (list.size() == 8) { printLocation(list); test.count++; } for (int i = startX; i < 8; i++) { Location location = new Location(i, startY); if (isLegalLoc(list, location)) { list.offer(location); eightQueen(list, 0, startY + 1); list.pollLast(); } } } private boolean isLegalLoc(LinkedList<Location> list, Location location) { for (Location each : list) { if (location.x == each.x || location.y == each.y || Math.abs(location.x - each.x) == Math.abs(location.y - each.y)) { return false; } } return true; } private void printLocation(LinkedList<Location> list) { for (Location each : list) { System.out.println(each.toString() + "\n"); } System.out.println(); } } class Location { int x; int y; Location(int x, int y) { this.x = x; this.y = y; } @Override public String toString() { return "(" + x + "," + y + ")"; } }
-
分支限界法
-
基本思想
- 是一种在问题的解空间树 T T T上搜索问题解的算法。
- 分支限界法与回溯法的求解目标不同。回溯法的求解目标是找出T中满足约束条件的所有解,
- 分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的解,即在某种意义下的最优解。
-
例子
-
问题
- 0-1背包问题
- 给定 n n n种物品和一背包。物品 i i i的重量是 w i w_i wi,其价值为 v i v_i vi,背包的容量为 c c c。
- 问应如何选择装入背包中的物品,使得装入背包中的物品的总价值最大?
-
解决方法
/* * 本代码实现了运用优先队列式分支限界法解决了01背包问题。解决问题的大致思想和前2篇博客的回溯法 * 大致相同,都属于搜索算法,不过实现方式上略有不同。对于子集树问题,利用优先队列式分支限界法 * 的关键之一就是要确定优先级的设置。在本代码中,优先级设置为每个节点处能够取到的价值上界。 * 对于寻找剩余物品的最高价值上界,按照背包中剩余空间依次取剩下的物品,当空间不足以取下一个 * 物品时,则将下一个物品的单位重量价值折算到现在的剩余空间中去计算理想最高上界。计算出某个 * 节点的上界后,比较上界和已经找到的最大值之间的关系。 * 当然,首先要背包中的物品按照单位重量价值进行排序,方便于后面右子树的剪枝操作。 * 在本代码中,省略了该排序过程,在初始化物品的重量和价值时,已经按照单位重量的价值排好了序。 * * 剪枝函数: * 对于向左搜索,可以通过是否超过背包容量和该节点价值上界能否超过最大值进行剪枝。 * 对于向右搜索,则可以用其父节点的上界减去本层物品的价值,即可得到右边节点的上界。 * */ import java.util.PriorityQueue; public class test { public static int n = 5; public static int capacity = 10; public static int[] weight = {2, 6, 4, 1, 5}; public static double[] value = {6, 9, 6, 1, 4}; public static int maxValue = 0; public static int[] bestWay = new int[n]; public static void main(String[] args) { Solution solution = new Solution(); solution.getMaxValue(); System.out.println("该背包能够取到的最大价值为:" + test.maxValue); System.out.println("取出的方法为:"); for (int i : test.bestWay) System.out.print(i + " "); } } class Solution{ public void getMaxValue() { PriorityQueue<thingNode> pq = new PriorityQueue<thingNode>(); //构造一个初始化节点,属于-1层 thingNode initial = new thingNode(); initial.level = -1; for (int i = 0; i < test.value.length ; i++) { initial.upProfit += test.value[i]; } pq.add(initial); while (!pq.isEmpty()) { thingNode fatherNode = pq.poll(); //当已经搜索到叶子节点时 if (fatherNode.level == test.n - 1) { if (fatherNode.value > test.maxValue) { test.maxValue = (int) fatherNode.value; for (int i = test.n - 1; i >= 0; i--) { test.bestWay[i] = fatherNode.left; fatherNode = fatherNode.father; } } } else { //先统计其左节点信息,判断是否加入队列。 if (test.weight[fatherNode.level + 1] + fatherNode.weight <= test.capacity) { thingNode newNode = new thingNode( test.weight[fatherNode.level + 1] + fatherNode.weight, fatherNode.value + test.value[fatherNode.level + 1], 1,fatherNode.level + 1,fatherNode); newNode.upProfit = new Solution().Bound(newNode); if (newNode.upProfit > test.maxValue) pq.add(newNode); } //向右节点搜索,其能够取到的价值上界通过父亲节点的上界减去本层物品的价值。 if ((fatherNode.upProfit - test.value[fatherNode.level + 1]) > test.maxValue) { thingNode newNode2 = new thingNode(fatherNode.weight,fatherNode.value, 0,fatherNode.level + 1,fatherNode); newNode2.upProfit = fatherNode.upProfit - test.value[fatherNode.level + 1]; pq.add(newNode2); } } } } //用于计算该节点的最高价值上界 public double Bound(thingNode no) { double maxLeft = no.value; int leftWeight = test.capacity - no.weight; int templevel = no.level; //尽力依照单位重量价值次序装剩余的物品 while (templevel <= test.n - 1 && leftWeight > test.weight[templevel]) { leftWeight -= test.weight[templevel]; maxLeft += test.value[templevel]; templevel++; } //不能装时,用下一个物品的单位重量价值折算到剩余空间。 if (templevel <= test.n - 1) { maxLeft += test.value[templevel] / test.weight[templevel] * leftWeight; } return maxLeft; } } //定义节点中的参数以及优先级设置的对象 class thingNode implements Comparable<thingNode> { int weight=0;//该节点目前背包中的重量 double value=0.0;//该节点目前背包中的总价值 double upProfit=0.0;//该节点能够达到的价值上界 int left=0; //该节点是否属于左节点(用于最终构造最优解) int level=-1; //该节点是第几个物品的选择 thingNode father=null; //该节点的父节点 thingNode(){ } thingNode(int weight,double value,int left,int level,thingNode father){ this.weight=weight; this.value=value; this.left = left; this.level = level; this.father = father; } public int compareTo(thingNode node) { if (this.upProfit < node.upProfit) return 1; else if (this.upProfit == node.upProfit) return 0; else return -1; } }
-
PRACTICE
CONCEPT
-
请用反证法证明 多源点最短路径问题 具有最优子结构性质。
-
设: P u v P_{uv} Puv 是从顶点 u u u 到顶点 v v v 的最短路径, w w w 是路径内部异于 u u u、 v v v 的任一点,则 P u w P_{uw} Puw 和 P w v P_{wv} Pwv 分别也是 u u u 到 w w w 和 w w w 到 v v v 的最短路径。
-
反证法证明:
-
若存在路径 P u w ′ P'_{uw} Puw′ 比 P u w P_{uw} Puw 更短, 且 P u w ′ P'_{uw} Puw′ 和 P w v P_{wv} Pwv 无关,利用 P u w ′ P'_{uw} Puw′ 替换 P u w P_{uw} Puw,与 P u v P_{uv} Puv 是从顶点 u u u 到顶点 v v v 的最短路径这一假设相冲突,故 P u w P_{uw} Puw 最短。
-
若存在路径 P u w ′ P'_{uw} Puw′ 比 P u w P_{uw} Puw 更短, 且 P u w ′ P'_{uw} Puw′ 和 P w v P_{wv} Pwv 有关,设存在公共点 x x x,将 P u w ′ P'_{uw} Puw′ 分解为 P u x ′ P'_{ux} Pux′ 和 P x w ′ P'_{xw} Pxw′,将 P w v P_{wv} Pwv 分解为 P w x ′ P'_{wx} Pwx′ 和 P x v ′ P '_{xv} Pxv′,则有 P u v ′ = P u x ′ + P x v ′ P'_{uv} = P'_{ux} + P'_{xv} Puv′=Pux′+Pxv′ ,与 P u v P_{uv} Puv 是从顶点 u u u 到顶点v 的最短路径这一假设相冲突。
-
综合上可知,与 P u w P_{uw} Puw 是子问题 u 到 w 的最短路径,同理可得,与 P w v P_{wv} Pwv 是从顶点 w w w 到顶点 v v v 的最短路径。所以多源点最短路径问题 具有最优子结构性质。
-
-
-
请比较 分治法与减治法 的相同点和差异点。
减治是分治的特殊情况。 相同点: 两种方法都需要将原问题分割成为子问题。 差异点: 分治法需要对每一个子问题进行求解,需要合并子问题的解; 减治法只需要对一个子问题进行求解,不需要合并子问题的解; -
请回答什么是平衡子问题?分治法与平衡子问题有什么样的关系。
平衡子问题是问题规模大致相同的子问题。 分治法就是将一个复杂的原问题分解为多个相似的平衡子问题, 再将子问题进行进一步的分解,直到最后的子问题可以简单的求解, 将这些子问题进行合并之后就得到原问题的解。 -
请问一般背包问题的贪心算法可以获得最优解吗?物品的选择策略是什么?
一般背包问题的贪心算法可以获得最优解,01背包问题不能通过贪心算法进行求解。 物品的选择策略是在容量允许的情况下优先选择 单位重量价值 最大的物品放入背包,从而获得背包问题的最优解。 -
请说明动态规划方法为什么需要最优子结构
最优子结构指大问题的最优解包含子问题的最优解。 动态规划是自底向上的计算各个子问题的最优解,利用子问题的最优解构造大问题的最优解。 -
请回答优先队列的问题。
优先队列可用什么数据结构实现? 堆 优先队列插入算法基本思想是什么? 在小根堆中,将元素x插至末尾,然后将x的关键字与其双亲关键字对比。 若x的关键字小于其双亲关键字,则进行交换,并继续这个流程。 直至x的关键字大于其双亲关键字或x没有双亲。 优先队列插入算法的时间复杂度? O(logn) -
动态规划算法的主要步骤是什么?
找出最优解的性质,描述其结构特征。 递归的定义最优值。 以自底向上的方式计算最优值。 根据最优解信息,构造最优解。 -
分治法所能解决的问题一般具有的特征?
问题划分到一定程度可以容易的解决。 问题可以划分为若干个平衡子问题,该问题具有最优的子结构性质。 子问题合并之后可以得到问题的解。 子问题是相互独立的。 -
*分支限界法的搜索策略是什么?
在扩展结点处,生成其所有的分支,然后从当前的活结点表中选择下一个扩展结点。 在每一个活结点处,计算其函数值,并根据函数值,从活结点表中选择最有利的结点。 使搜索方向向解空间上有最优解的分支推进,从而得到最优解。 分类 队列式分支限界法和优先队列式分支限界。 -
最坏时间复杂度和平均时间复杂度?
当问题规模n固定时, 输入不同的实例中最坏的时间复杂度。 输入不同的实例,所有实例的时间复杂度的平均。W ( n ) = m a x T ( n , I ) , I ∈ D n W(n) = max{T(n,I)}, I\in D_n W(n)=maxT(n,I),I∈Dn
W ( n ) = 1 l e n g t h ( D n ) ∑ I D n m a x T ( n , I ) , I ∈ D n W(n) = \frac{1}{length(D_n)}\sum^{D_n}_I max{T(n,I)}, I\in D_n W(n)=length(Dn)1I∑DnmaxT(n,I),I∈Dn
-
简述折半查找算法的基本实例?
设输入一个增序数组A[i:j]和目标元素x,选取mid=(i+j)/2,如果A[mid]=x,则返回mid。 如果A[mid]<x,则在A[i:mid-1]中继续寻找x,否则在A[mid+1:j]中继续寻找x。 以上过程反复使用,直至找到x,或是数组为空。 -
背包问题中目标函数和贪心算法的最优化度量相同吗?
不相同, 目标函数:最大利益。 最优化度量: 最大利益/重量比。 -
*可以使用回溯法求解的问题,解如何表示?有什么规定?
解可以表示为 n n n 元组 ( x 1 , x 2 , . . . , x n ) , x i ∈ S i (x_1,x_2,...,x_n),x_i \in S_i (x1,x2,...,xn),xi∈Si , S i S_i Si 是有穷集合,
( x 1 , x 2 , . . . , x n ) , x i ∈ S i (x_1,x_2,...,x_n),x_i \in S_i (x1,x2,...,xn),xi∈Si 具有完备性,则 ( x 1 , x 2 , . . . , x i ) , i < n (x_1,x_2,...,x_i),i<n (x1,x2,...,xi),i<n 一定合理。
-
回溯法的搜索特点是?
在解空间树上进行跳跃性的深度搜索,使用判定函数考察x[k], 如果x[k]合理,就继续考察x[k]的子树,当考察x[k]结束后,回溯到x[k-1]。 -
在8皇后问题中回溯法的判别函数place的基本流程是什么?
将第k行的皇后和前k-1行的皇后进行判定,如果合理就返回true,不合理就返回false。 -
分治法一般用到递归调用?
当问题的规模比较大的时候,必然要将问题划分平衡子问题, 当子问题的规模仍然很大时,需要反复分治,必然用到递归。 -
分析最坏时间复杂度的必要性?
最坏时间复杂度决定算法的优劣, 最坏时间复杂度较平均时间复杂度有可操作性。 -
简述渐进时间复杂度上界 O O O 的定义。
O : T ( n ) = c ∗ g ( n ) 形式的不等式,使得在 n ≥ n 0 的条件下 , 满足 0 ≤ T ( n ) ≤ c ∗ g ( n ) 。( n 0 是自己取的一个数) O:T(n) = c * g(n)形式的不等式,使得在n ≥ n_0的条件下,\\ 满足0 ≤ T(n) ≤ c * g(n)。(n_0是自己取的一个数)\\ O:T(n)=c∗g(n)形式的不等式,使得在n≥n0的条件下,满足0≤T(n)≤c∗g(n)。(n0是自己取的一个数)f ( n ) = 2 n + 3 , 且 n 0 = 1 ≤ n , 有 c ∗ g ( n ) = 2 n + 3 n ≥ 2 n + 3 ≥ 0 , 则 g ( n ) = n . 则 f ( n ) = O ( g ( n ) ) = O ( n ) . f(n)=2n+3,且n_0=1\le n,\\ 有c*g(n)=2n+3n\ge 2n+3 \ge 0,则g(n)=n.\\ 则f(n)=O(g(n))=O(n). f(n)=2n+3,且n0=1≤n,有c∗g(n)=2n+3n≥2n+3≥0,则g(n)=n.则f(n)=O(g(n))=O(n).
-
二分检索检索算法的最多比较次数?
设计数组长度为n,则最多的比较次数为logn。 -
快速排序算法的最坏情况需要多少次比较运算?
最坏情况下快速排序退化为冒泡排序,需要比较n^2次。 -
贪心算法的基本思想?
根据一种最优度量依次选择输入的分级处理方法。 基本思路: 选取最优化度量,按照度量将输入进行排序, 依次将输入加入部分解中,直至不满足约束条件。 -
回溯法的隐约束一般指什么?
元素之间应满足的某种关系。 -
阐述归并排序的分治思路?
将数组分成两部分,对这两部分分别进行排序,然后将排序好的两部分归并成一个有序序列。 如果数组划分之后仍然很大,则继续划分,直至数组长度为1. -
快速排序的基本思想是什么。
在待排序的N个记录中任意取一个记录,把该记录放在最终位置后,数据序列被此记录分成两部分。 所有关键字比该记录关键字小的放在前一部分,所有比它大的放置在后一部分,并把该记录排在这两部分的中间,这个过程称作一次快速排序。 重复上述过程,直到每一部分内只有个记录为止。 -
什么是直接递归和间接递归?消除递归一般要用到什么数据结构?
在定义一个函数的时候又出现了调用本过程或者函数的成分,直接递归。 如果过程或者函数P调用过程或者函数Q,Q又调用P,这个称为间接递归。 消除递归一般要用到栈这种数据结构。 -
什么是哈密顿环问题?
哈密顿环是指一条沿着图G的N条边环行的路径,它的访问每个节点且返回它的开始位置。 -
用回溯法求解哈密顿环,如何定义判定函数?
选择的节点 X [ k ] X[k] X[k]是从未到过的节点,且 D ( X [ k − 1 ] , X [ k ] ) ≠ ∞ D(X[k-1],X[k])≠∞ D(X[k−1],X[k])=∞,如果 k = − 1 k=-1 k=−1,则 C ( X [ k ] , X [ 1 ] ) ≠ 0 C(X[k],X[1])≠0 C(X[k],X[1])=0 。
-
请写出prim算法的基本思想。
最初生成树T为空,依次向内加入与树有最小邻接边的n-1条边。 最小代价的一条边到T,根据各节点到T的邻接边排序,选择最小边加入, 重复以上步骤,直至加入n-1条边。
CALATION*
-
假设函数 f 1 , f 2 , f 3 f_1,f_2,f_3 f1,f2,f3 的处理时间分别为 O ( n ) , O ( n 2 ) , O ( 1 ) O(n),O(n^2),O(1) O(n),O(n2),O(1),分析以下代码的时间复杂度。
# T(n) = max(O(n),O(n^2)) + (n-1)*O(1) = O(n^2) procedure A1(int n, b) if b < 3 then f1 else f2 for i=1 to n-1 do f3 end # n > 1 T(n)= T(n-1) + O(n) = T(n-2) + 2*O(n) = T(1) + n*O(n) = O(n^2) # n == 1 T(n)=O(1) procedure A2(int n) if n=1 then return f3 else A2(n-1) f1 end # n=1 O(1) # n>1 T(n) = T(n-1) + O(n) = (n-1)O(n) + O(1) = O(n^2) -
用动态规划法求如下 0/1 背包问题的最优解:有5个物品,其重量分别是(3,2,1,4,5),价值分别是(25,20,15,40,50),背包容量为 6。 写出求解的过程。
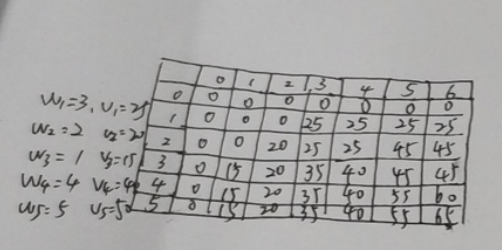
首先求解初始子问题: 将前面i个物品放入到容量为0的背包, 和把0个物品放入容量为j的背包中。 即v(i,0)=v(0,j)=0 再求解第一个阶段的子问题,只放入前1个物品,确定各种容量情况下,背包所能够背负的最大价值。 w1=3>1,则v(1,1)=0,v(1,3)=max(v(0,3),v(0,3-w1)+v1)=25,依次计算填写第1行。 再求解第二个阶段的子问题,只放入前2个物品,确定各种容量情况下,背包所能够背负的最大价值。 w1=2>1,则v(2,1)=0,v(2,2)=max(v(1,2),v(1,2-w2)+v2)=20,依次计算填写第2行。 再求解第三个阶段的子问题,只放入前3个物品,确定各种容量情况下,背包所能够背负的最大价值。 w1=2>1,则v(2,1)=0,v(2,2)=max(v(1,2),v(1,2-w2)+v2)=20,依次计算填写第3行。 依次类推,v(5,6)为往背包容量为6的背包中,从5个物品选择的放入,以达到v(5,6)最大 为了求物品编号,从v(5,6)开始回溯。。。。。 因为v(5,6) > v(4,6), 所以物品5进入背包。 -
写出多段图最短路径动态规划算法求解下列实例的过程,并求出最优值。
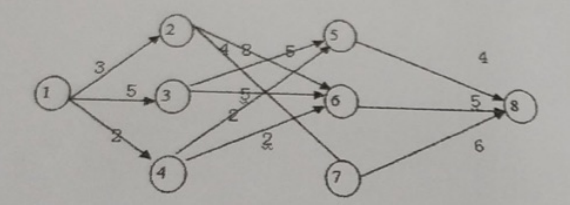
从节点1出发,d(1,2)=3,d(1,3)=5,d(1,4)=2。
d(1,5)=
d(1,3)+c35=10
d(1,4)+c45=4 *
d(1,6)=
d(1,2)+c26=11
d(1,3)+c36=10
d(1,4)+c46=4 *
d(1,7)=
d(1,2)+c27=7 *
d(1,8)=
d(1,5)+c58=8 *
d(1,6)+c68=9
d(1,7)+c78=13
综上所述,多段图最短路径动态规划算法得出的最短路径是1-4-5-8。
-
最长升序子序列问题。
[ 1 , 7 , 3 , 5 , 9 , 4 , 8 ] [1,7,3,5,9,4,8] [1,7,3,5,9,4,8] 中的最长升序子序列 [ 1 , 3 , 5 , 8 ] [1,3,5,8] [1,3,5,8]
f ( i ) = { 1 i = 1 m a x { f ( j ) + 1 : a [ j ] < a [ i ] } i > 1 1 a [ i ] < a [ k ] , k ∈ b e f o r e , i > 1 f(i)=\left\{ \begin{matrix} 1&i=1\\ max\{f(j)+1: a[j]<a[i]\}&i>1\\ 1& a[i]<a[k],k\in before,i>1 \end{matrix} \right. f(i)=⎩ ⎨ ⎧1max{f(j)+1:a[j]<a[i]}1i=1i>1a[i]<a[k],k∈before,i>1 -
kruaskal 求 G G G 的最小生成树。
在连接两个不同连通分量的边中选权值最小的边。
基本思想:每次都在连接两个不同连通分量的边中选权值最小的边,将其放入生成树中,直到生成树中有n-1条边。
时间复杂度 O ( e l o g e ) O(eloge) O(eloge)
-
作业调度
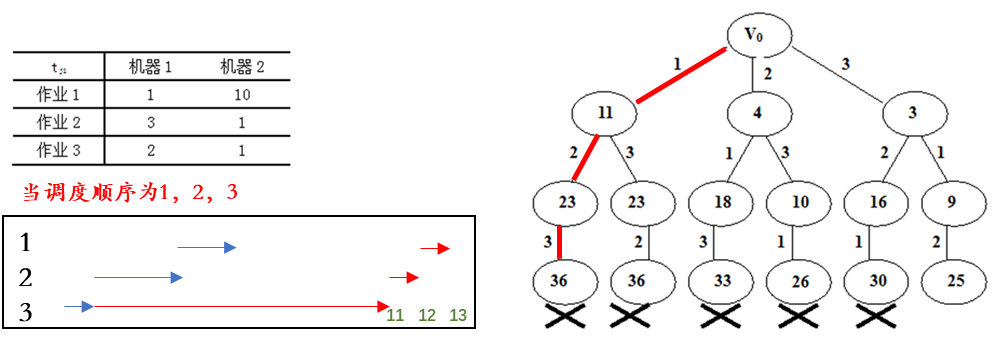
剪枝策略,当前时间 t 1 > = t b e s t t_1 >= t_{best} t1>=tbest , 则剪枝。
-
格雷码构造问题
“格雷码” 是一个长度为2”的序列,满足: (a)每个元素都是长度为n比特的串 (b)序列中无相同元素 (c)连续的两个元素恰好只有1个比特不同 (d)元素个数为2^n 例如: n=2时,格雷码为{00,01,11,10}。 解决 用分治法解决。 当n=1时,输出格雷码{0,1} 当n>1时,格雷码的长度为2^n,即共有2^n个码序列。 问题一分为二,即上半部分和下半部分。 上半部分最高位设为0,下半部分最高位设为1。 重复以上步骤,构造n-1位的格雷码。 -
Dijkstra

迭代 S u d[2] d[3] d[4] d[5] 初始 1 - 10 30 100 1 1,2 2 10 60 30 100 2 1,2,4 4 10 50 30 90 3 1,2,4,3 3 10 50 30 60 4 1,2,4,3,5 5 10 50 30 60 -
0-1背包问题
n=6,c=20,price=[4,8,15,1,6,3],weight=[5,3,2,10,4,8] 进一步计算 p/w=[0.8,2.6,7.5,0.1,1.5,0.37] 然后按单位重量物品价值的顺序逐个将物品放到背包中,直至放不下为止。 -
最大子段和问题。
将所给定序列 a [ 1 : n ] a[1:n] a[1:n] 分为长度相等的两段 a [ 1 : n / 2 ] a[1:n/2] a[1:n/2] 和 a [ n / 2 + 1 : n ] a[n/2+1:n] a[n/2+1:n] , 分别求
出这两段的最大子段和,则 a [ 1 : n ] a[1:n] a[1:n] 的最大子段和有哪三种情形?
(1) a [ 1 : n ] a[1:n] a[1:n] 的最大子段和与 a [ 1 : n / 2 ] a[1:n/2] a[1:n/2] 的最大子段和相同。
(2) a [ 1 : n ] a[1:n] a[1:n] 的最大子段和与的最大子段 a [ n / 2 + 1 : n ] a[n/2+1:n] a[n/2+1:n] 和相同。
(3) a [ 1 : n ] a[1:n] a[1:n] 的最大子段和为 ∑ a k ( i = < k < = J ) \sum a_k(i=<k<=J) ∑ak(i=<k<=J)且 1 < = i < = n / 2 , n / 2 + 1 < = J < = n 1<=i<=n/2, n/2+1<=J<=n 1<=i<=n/2,n/2+1<=J<=n. -
写出maxmin算法对下列实例中找最大数和最小数的过程。
数组 `A=(48,12,61,3,5,19,32,7)` 48,12,61,3 5,19,32,7 61,48 12,3 32,19 7,5 61,32 5,3 61,3 -
快速排序的例子
快速排序算法对下列实例排序,算法执行过程中,写出数组A第一次被分割的过程。 A=(65, 70, 75, 80, 85, 55, 50, 2)
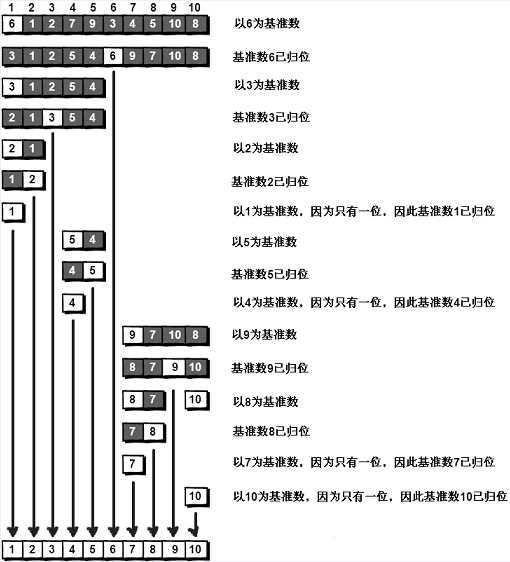
-
归并排序算法对下列实例排序,写出算法执行过程。
数组 `A=(48,12,61,3,5,19,32,7)` 48,12 61,3 5,19 32,7 12,48 61,3 5,19 7,32 3,12,48,61 5,7,19,32 3,5,7,12,19,32,48,61
CODE
prim&dijkstra&kruskal
djkstra求单源最短路径
floyd求任意-对结点的最短路径
prim、kruscal求 最小生成树
bellman求有负环的单源最短路径
prim算法以点为中心往四周扩散,每个结点只访问一次,往四周扩散时,贪心地选择容易去的结
点,但是不会去那些已经被”组织”按了的结点(都是内部成员了,就没必要再发展了)。星
之火,可以燎原,最终产生一个最小生成树。 prim创建的是一个人人平等的社会。
djkstra算法以点为中心往四周扩散, 一个结点可能会访问多次,往四周扩散时,贪心选择那些容易
的结点,但是会去那些已经被”组织”招按了的结点,因为那些人虽然已经被组织招安了,实
际上”领导”(单源结点)对他的控制力不够强(领导到它的距离太远了) , 所以需要巩固,所以
可以更新该点到"领导” 的最短路径。djkstra创建的是一 个有"领导” 的社会。
kruscal算法就比较简单了。kruscal每次都选图中最短的那条边(只要这条边能够不和已选边产生
环即可)。kruscal就像群雄并起,各地爆发了规模不一的起义一样,群雄逐鹿。在整个起义过程
中,起义军不断融合,最终组成了一支横跨整个图的军队。
prim算法注重点,kruscal注重边。
prim算法翻于点少边多(稠密)的情况,kruscal适用于点多边少(稀疏)的情况。
实现上, prim算法常常使用优先队列,kruscal常常用到并查集。
分治法
-
旅行家的预算
-
问题
- 一个旅行家驾驶汽车以最少的费用从一个城市到另一个城市
- (假设出发时油箱是空的)。
- 给定两个城市之间的距离 D D D、汽车油箱的容量 C C C(以升为单位).
- 每升汽油能行驶的距离 B B B、
- 出发点每升汽油价格P和沿途油站数 0 ≤ N ≤ 100 0\leq N\leq100 0≤N≤100,
- 油站 i i i 离出发点的距离 D i D_i Di、每升汽油价格 P i ( i = l , 2... N ) P_i(i=l,2...N) Pi(i=l,2...N)。
- 结果
- 四舍五入至小数点后两位。
- 如果无法到达目的地,则输出
No solution。
- 一个旅行家驾驶汽车以最少的费用从一个城市到另一个城市
-
解决方法
class Solution { public double travellerBudget(double distance, double capacity, double effect, double price, int stations, double[][] stationsInfo) { double achieve = capacity * effect; double ans = 0.0; double[] currentStates = new double[]{0.0, price}; double nextPrice = 0x1.fffffffffffffP+1023; int nextIndex = -1; for (int i = 1; i < stations; i++) { if (nextPrice > stationsInfo[i][1]) { nextPrice = stationsInfo[i][1]; nextIndex = i; } if (stationsInfo[nextIndex][1] < currentStates[1] || (i + 1 < stations && stationsInfo[i + 1][0] > (currentStates[0] + achieve))) { ans += (stationsInfo[nextIndex][0] - currentStates[0]) / effect * currentStates[1]; currentStates = stationsInfo[nextIndex]; nextPrice = 0x1.fffffffffffffP+1023; } } // 便宜的站点。 return new BigDecimal(ans).setScale(2, BigDecimal.ROUND_HALF_UP).doubleValue(); } }
-
-
贷款利率
-
问题
- 当一个人从银行贷款后,在一段时间内他(她)将不得不每月偿还固定的分期付款。
- 这个问题要求计算出贷款者向银行支付的利率。假设利率按月累计。
- 国家规定月利率不得大于2.5%
- 输入
- 第一个整数表示贷款的原值 a a a,
- 第二个整数表示每月支付的分期付款金额 b b b,
- 第三个整数表示分期付款还清贷款所需的总月数 m m m。
- ( 1 < a , b < 1 0 9 , 1 < m < 1 0 4 ) (1<a,b<10^9,1<m<10^4) (1<a,b<109,1<m<104)
-
解决方法
public class test { public static void main(String[] args) { Solution solution = new Solution(); double ans = solution.bankLoans(1000.0, 100.0, 12); System.out.println(String.format("%.2f", ans)); } } class Solution { public double bankLoans(double loan, double repayment, int moths) { double l = 0.0; double r = 5.0; for (int i = 0; i < 100; i++) { double mid = (r + l) / 2; if (check(mid / 100.0, loan, repayment, moths)) { l = mid; } else { r = mid; } } return l; } private boolean check(double value, double loan, double repayment, int moths) { double sum = loan; for (int i = 1; i <= moths; i++) { sum = sum * (1 + value) - repayment; } return sum <= 0; } }
-
Q&A
T ( n ) T(n) T(n) 是渐进时间复杂度
当问题的规模n趋向于无穷大时,影响算法效率的因素是T(n)的数量级。
而其他因素只会影响算法效率的常数倍。
因此可以用T(n)的数量级评价算法,时间复杂性T(n)的数量级来评价算法的效率。
算法复杂度渐进符号
| 记号 | 含义 | 通俗理解 |
|---|---|---|
| (1)Θ(西塔) | 渐进紧确界 | 相当于"=" |
| (2)O (大欧) | 渐进上界 | 相当于"<=" |
| (3)o(小欧) | 非渐进紧确的上界 | 相当于"<" |
| (4)Ω(大欧米伽) | 渐进下界 | 相当于">=" |
| (5)ω(小欧米伽) | 非渐进紧确下界 | 相当于">" |
O-一个函数的上限
Omega-一个函数的下限
Theta-一个函数的平均界限
$$
O:f(n) = c * g(n)形式的不等式,使得在n ≥ n_0的条件下,\
满足0 ≤ f(n) ≤ c * g(n)。(n0是自己取的一个数)\
\Omega:f(n) = c * g(n)形式的不等式,使得在n ≥ n_0的条件下,\
满足0 ≤ c * g(n) ≤ f(n) 。(n0是自己取的一个数)\
\Theta:f(n) = c * g(n)形式的不等式,使得在n ≥ n_0的条件下,\
满足0 ≤ c * g(n) ≤ f(n) 。(n0是自己取的一个数)\
$$
- 例子
f ( n ) = 2 n + 3 , 且 n 0 = 1 ≤ n , 有 c ∗ g ( n ) = 2 n + 3 n ≥ 2 n + 3 ≥ 0 , 则 g ( n ) = n . 则 f ( n ) = O ( g ( n ) ) = O ( n ) . f(n)=2n+3,且n_0=1\le n,\\ 有c*g(n)=2n+3n\ge 2n+3 \ge 0,则g(n)=n.\\ 则f(n)=O(g(n))=O(n). f(n)=2n+3,且n0=1≤n,有c∗g(n)=2n+3n≥2n+3≥0,则g(n)=n.则f(n)=O(g(n))=O(n).
f ( n ) = 2 n + 3 , 且 n 0 = 1 ≤ n , 有 0 ≤ c ∗ g ( n ) = l o g n ≤ 2 n + 3 , 则 g ( n ) = l o g n . 则 f ( n ) = Ω ( g ( n ) ) = Ω ( l o g n ) . f(n)=2n+3,且n_0=1\le n,\\ 有0 \le c*g(n)=logn\le 2n+3,则g(n)=logn.\\ 则f(n)=\Omega(g(n))=\Omega(logn). f(n)=2n+3,且n0=1≤n,有0≤c∗g(n)=logn≤2n+3,则g(n)=logn.则f(n)=Ω(g(n))=Ω(logn).
f ( n ) = 2 n + 3 , 且 n 0 = 1 ≤ n , 有 c ∗ g ( n ) = 2 n + 3 n ≥ 2 n + 3 ≥ n , 此时不等式两边都为 n , 则 g ( n ) = n . 则 f ( n ) = Θ ( g ( n ) ) = Θ ( n ) . f(n)=2n+3,且n_0=1\le n,\\ 有 c*g(n)=2n+3n\ge 2n+3 \ge n,此时不等式两边都为n,则g(n)=n.\\ 则f(n)=\Theta(g(n))=\Theta(n). f(n)=2n+3,且n0=1≤n,有c∗g(n)=2n+3n≥2n+3≥n,此时不等式两边都为n,则g(n)=n.则f(n)=Θ(g(n))=Θ(n).
other
-
动态规划-0/1背包问题
多项式级别 最优子结构性质 问题的最优解包含子问题的最优解 子问题重叠性质 备忘录方法 具有某种最优性质 -
Prim算法
作用 使用贪心策略求解最小生成树问题 -
回溯法-背包问题
策略 深度优先 作用 对问题的机解空间树进行搜索,寻求答案。 -
分支限界算法-单源最短路径
策略 广度优先 组成 队列式分支限界法 优先 队列式分支限界法 -
分治法-二分搜索
O(logn) -
贪心算法-背包问题
方式 自顶而下 -
概率算法
组成 蒙特卡罗算法 拉斯维加斯算法 舍伍德算法 投点法 -
线性规划问题
定义 -
旅行商问题
可以用 回溯法、分支限界、NP完全性理论和近似算法 -
最长上升子序列问题
f ( i ) = m a x { f ( j ) + 1 } , 1 < = j < i , a [ j ] < a [ i ] f(i) = max\{f(j)+1\}, \\ 1<=j<i, a[j] < a[i] f(i)=max{f(j)+1},1<=j<i,a[j]<a[i] -
Kruskal