有一个无穷大的二维网格图，一开始所有格子都未染色。给你一个正整数 n ，表示你需要执行以下步骤 n 分钟：

第一分钟，将任一格子染成蓝色。

之后的每一分钟，将与蓝色格子相邻的 所有 未染色格子染成蓝色。

下图分别是 1、2、3 分钟后的网格图。

请你返回 n 分钟之后 被染色的格子 数目。

题目链接：https://leetcode.cn/problems/count-total-number-of-colored-cells

今天刷到这题，觉得有意思。在纸上画的麻烦，搞个excel涂色，还挺减压的，就像这样：

n=1时，红色1

n=2时，多了橙色，1 + 4 = 5

n=3时，多了绿色，5 + 8 = 13

n=4时，多了紫色，13 + 12 = 25

观察下，规律来了：

n=1时，红色1 = 1  + （1 - 1）* 4  

n=2时，多了橙色，1 + 4 = 5 = 1  + （2 - 1）* 4  

n=3时，多了绿色，5 + 8 = 13 = 5  + （3 - 1）* 4  

n=4时，多了紫色，13 + 12 = 25 = 13  + （4 - 1）* 4

那么公式，就是: 后一个数 = 前一个数 + （n-1）*4  

这让人联想到类似斐波拉契数组的解法，F(n) = F(n-1) + (n-1) * 4

于是代码如下，可见非常低效，因为太多重复计算了。

既然都知道公式了，可以把公式用作 DP 动态规划转移方程，可以将粗暴递归的重复计算变成线性的 O(n) 规模。

于是代码如下：

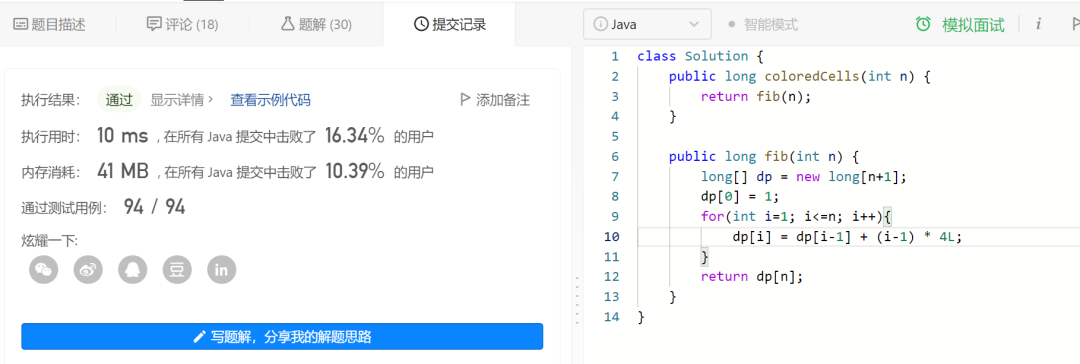
有一点点提升

发大招，上数学归纳法

这是我家女神帮我算的，我这学渣不懂，说是什么高斯定理，高斯是谁？大家知道吗？

（什么？字不好看？风大听不见，你再说一遍？哦哦，没关系，人漂亮啊）

管他呢，现在有了公式，代码就只要一行了，秀的简直不行不行的。

感受下，击败100%

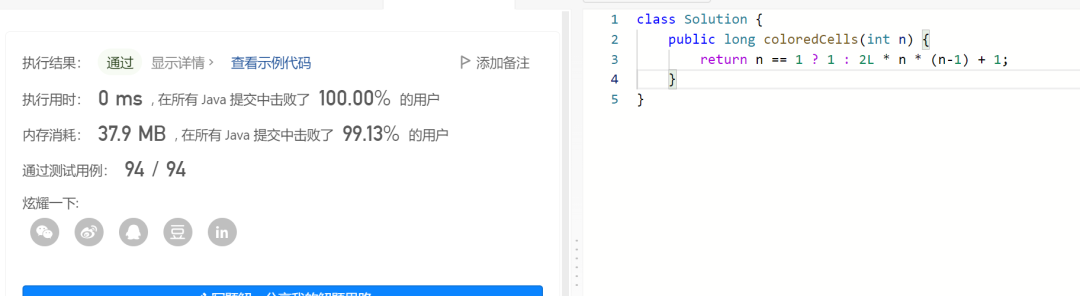
数学好，就是秒杀全场，什么迭代，什么动态规划，都不在话下。

所以，同学们，弟弟妹妹们，还是好好学数学吧。

当然，还有一个 excel 图像法，我不会推公式，我会画图，小学数学老师教的 “加辅助线” ，加辅助线也能推导出用高斯推导出来的那个啥公式，你看看。

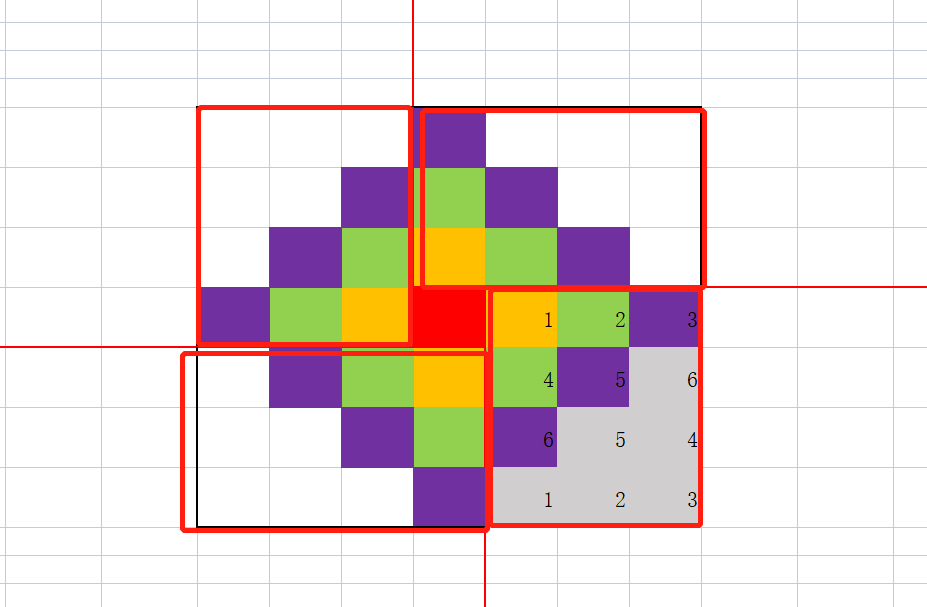
四条红色的辅助线，把图像分成了四个大红块，加中间一个小红块

中间一个小红块就是1

大红块的规律，看右下角，标了数字，好数。

这是 n = 4 时候的图，长方形的面积等于长乘以宽，4乘以3，然后去掉灰色的恰好是一半，4*3/2，那么得到公式就是（n-1）乘以 n 乘积的一半。

那么最终的公式就是：

F(n) = 4 个大红块面积的一半 + 1 个小红块 

       = 两个大红块面积 + 1个小红块

       = 2 * n  *（n-1） + 1

所以，图形化的学数学，简直太棒了。（这点建议希望数学老师参考下哈，不然学得没有趣味，还会有很多我这样的学渣 ）