【机会约束、鲁棒优化】具有排放感知型经济调度中机会约束和鲁棒优化研究【IEEE6节点、IEEE118节点算例】（Matlab代码实现）

news2024/10/1 7:43:47

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

2.1 风能

2.2 IEEE6和IEEE118

2.3 IEEE6

2.4 IEEE118

🎉3 参考文献

🌈4 Matlab代码及数据实现

💥1 概述

机会约束规划(chance constrained programming简称CCP)也称为概率约束规划,最初由Charnes和 Cooper[1在1958年提出,是针对约束条件中含有随机参数并在一定概率条件满足下的最优化问题.近几十年,机会约束广泛应用于参数不确定的优化和决策问题中.比如,网络优化2]、供应链管理3、生产计划[4和水流箱管理5等．关于CCP的发展情形,感兴趣的读者可参见综述文献[6].机会约束规划的一般形式为:

常规机会约束假设已知随机变量概率分布Р的准确信息.然而,在许多实际应用中随机变量∈ 难以精确预测,仅能够获得其部分信息(如矩和样本信息等).满足这些概率信息的分布构从伏)方法结合.建立在分布不确定集合最环情优L好分布鲁棒优化问题优化思想和随机优化方法结合,建立在分布不确定
鲁棒优化(distributionally robust optimization,简称结合机会约束即为分布鲁棒机会约束优化问题(distributionally robust chance constrainedoptimization program,简称DRCC).
分布鲁棒机会约束优化的一般形式为:

调度者存在多元化的风险偏好，导致对“最恶劣场景”的评估产生差异。如图 3 所示，日前预测

总偏差由偏离时长和对应时刻的偏离度决定。也就是说，控制调度周期内不确定变量的总体偏离度，就能够度量调度者风险偏好。但是，在给定的总偏离度条件下，学界普遍认为“最恶劣场景”发生在不确定域边界，这在线性系统中必然成立，但是在非线性系统中，“最恶劣场景”可能发生在不确定域内。

为此，本文通过有限离散化不确定域，生成梯次偏离的不确定域边界，扩充“恶劣场景集”。在此基础上，控制不确定变量的总体偏离值，表征调度者的保守程度。

考虑风电不确定性的电力系统调度模型中的部分输入量（Pw和Pg）具有不确定性，通过传统数学规划方法得到的优化调度方案可能无法实现系统的经济性最优，甚至可能违反系统的安全运行约束。针对传统的数学规划方法难以消除不确定参量对优化模型的负面影响，Soyster提出了鲁棒优化方法。RO在优化模型建立之初就对其中的不确定参量进行分析，明确不确定参量的波动区间。RO旨在得到这样一个优化方案:在不确定参量可能的取值范围内，优化模型的所有约束条件都能被满足，且使得优化模型目标函数能取得最恶劣情况下的最优值。因此，RO所得的优化结果对不确定参量的波动具有免疫能力，并且不失良好性能。

对包含不确定参量的优化问题而言，RO提出了一种“劣甲选优的处理刀八，关注点在于最恶劣情况下模型的最优解，仅需知道不确定参量波动的边界信息即可进行决策，计算效率高，需要了解的不确定参量信息少，优化方案的抗干扰能力强，因此具有很高的实用价值。RO的提出和发展弥补了传统优化方法的不足，己成为处理含有不确定参量优化问题的重要工具。

传统的数学优化模型一般形式如下:

📚2 运行结果

2.1 风能

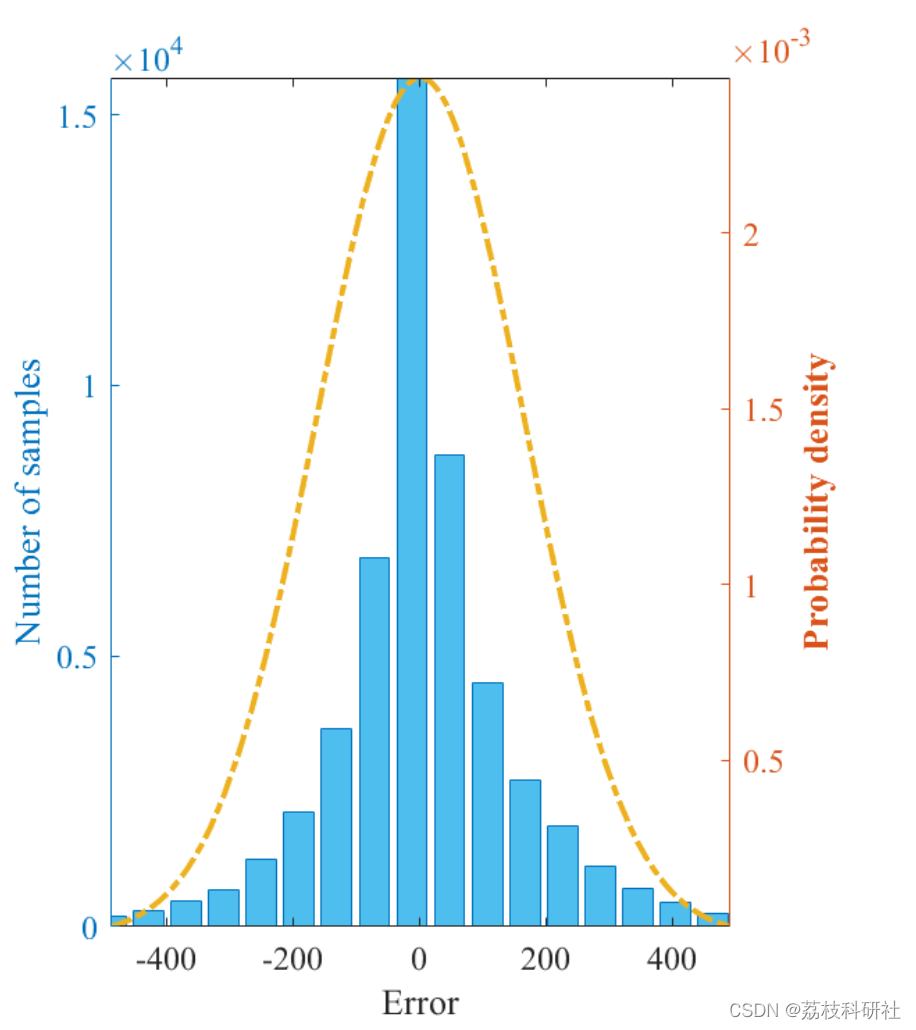
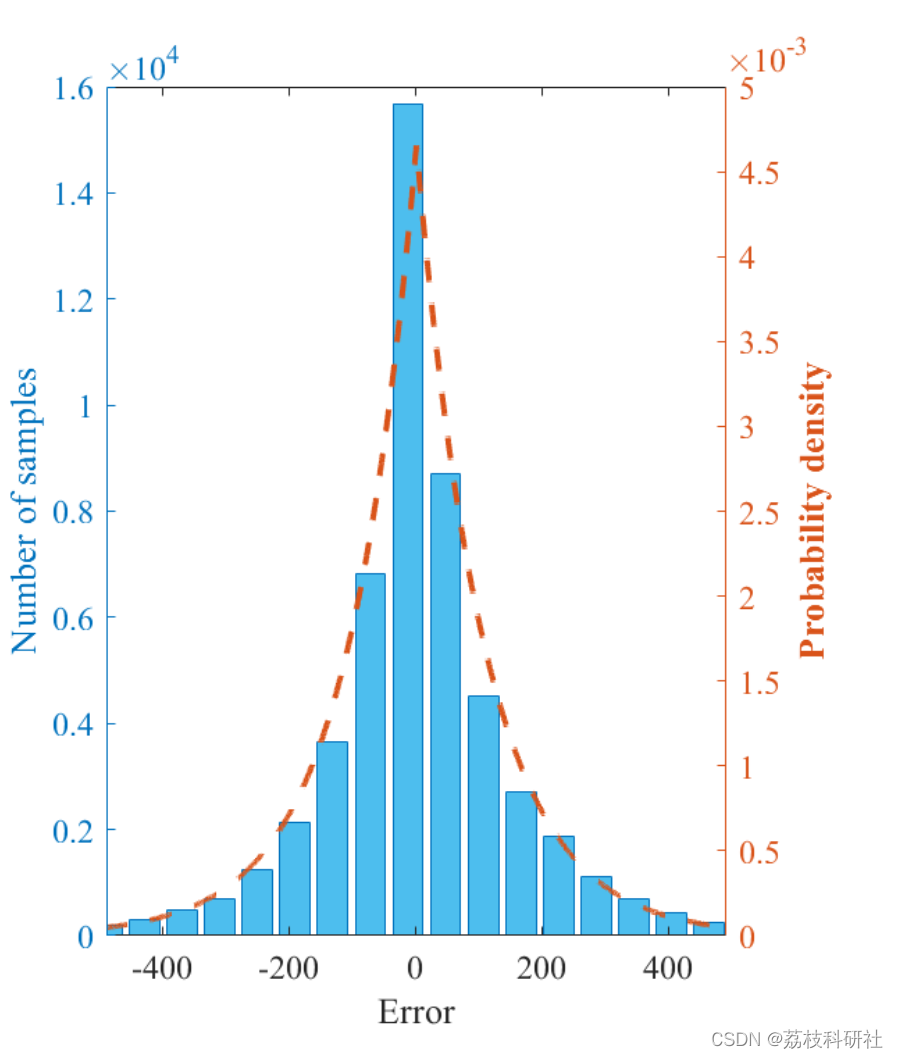
部分代码：

figure
yyaxis left
bar(x,y,'FaceColor','[0.3010 0.7450 0.9330]','EdgeColor','[0 0.4470 0.7410]');box off
xlim([mu-3*sigma,mu+3*sigma])
xlabel('Error','FontSize',13.2,'FontName','Times New Roman','FontWeight','Bold')
ylabel('Number of samples','FontSize',13.2,'FontName','Times New Roman','FontWeight','Bold')
% a2=axes;
yyaxis right
fp=fplot(@(x)normpdf(x,mu,sigma),[mu-3*sigma,mu+3*sigma]);
xlim([mu-3*sigma,mu+3*sigma])
fp.LineStyle = '-.';
fp.LineWidth =2;
fp.Color =[0.9290 0.6940 0.1250];
%set(a2,'box','off','yaxislocation','right','color','none')
% set(gca,'xticklabel',[]);
ylabel('Probability density','FontSize',13.2,'FontName','Times New Roman','FontWeight','Bold')
set(gcf,'Position',[100 100 400 500]);
set(gca,'FontSize',12,'FontName','Times New Roman')
ax = gca;
ax.YAxis(1).Exponent = 4;

2.2 IEEE6和IEEE118

x=[1,2,3,4];
b=BarPlotBreak(x,y_time_record',15,20,'Line',0.99);
x_label={'CC (Gaussian)','DRO (Binomial)','Clairvoyant','SO (Scenario)'};
set(gca,'XTickLabel', x_label)
legend('6 bus','118 bus')
ylabel('time (s)','FontSize',13.2,'FontName','Times New Roman','FontWeight','Bold')
set(gca,'FontSize',12,'FontName','Times New Roman')
b(1).FaceColor=[0.9290, 0.6940, 0.1250];
b(2).FaceColor=[0.4660, 0.6740, 0.1880];

2.3 IEEE6

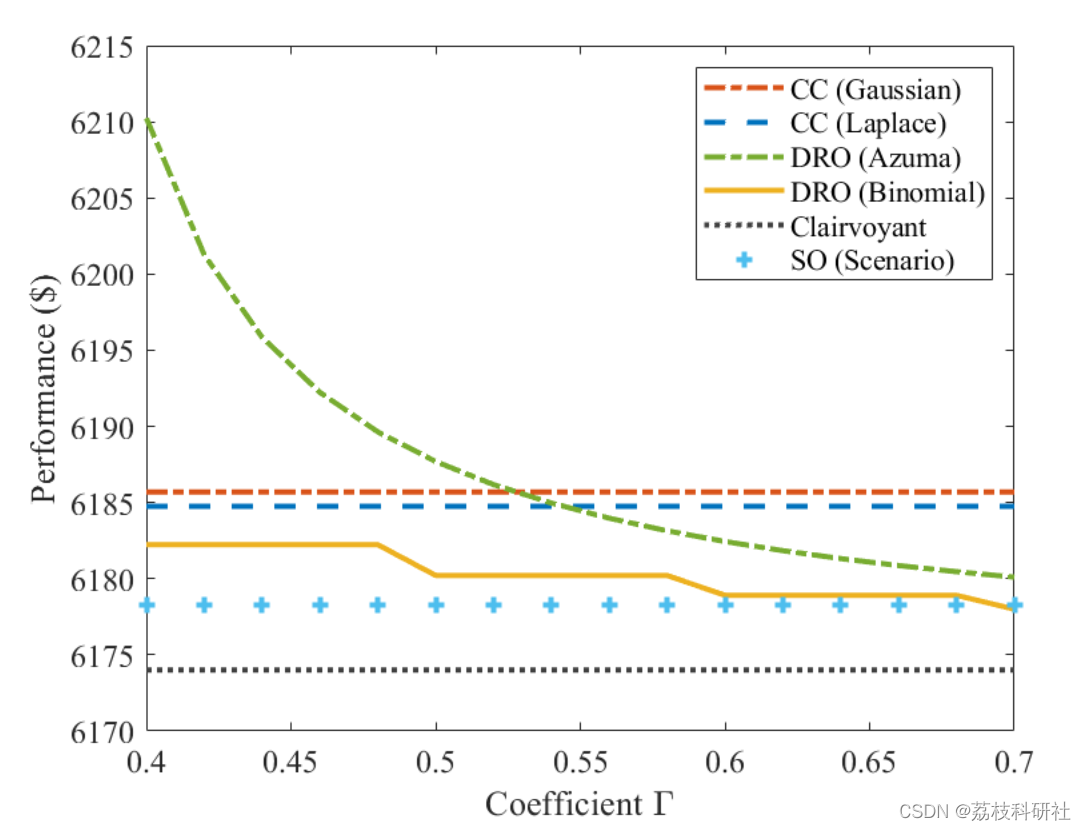
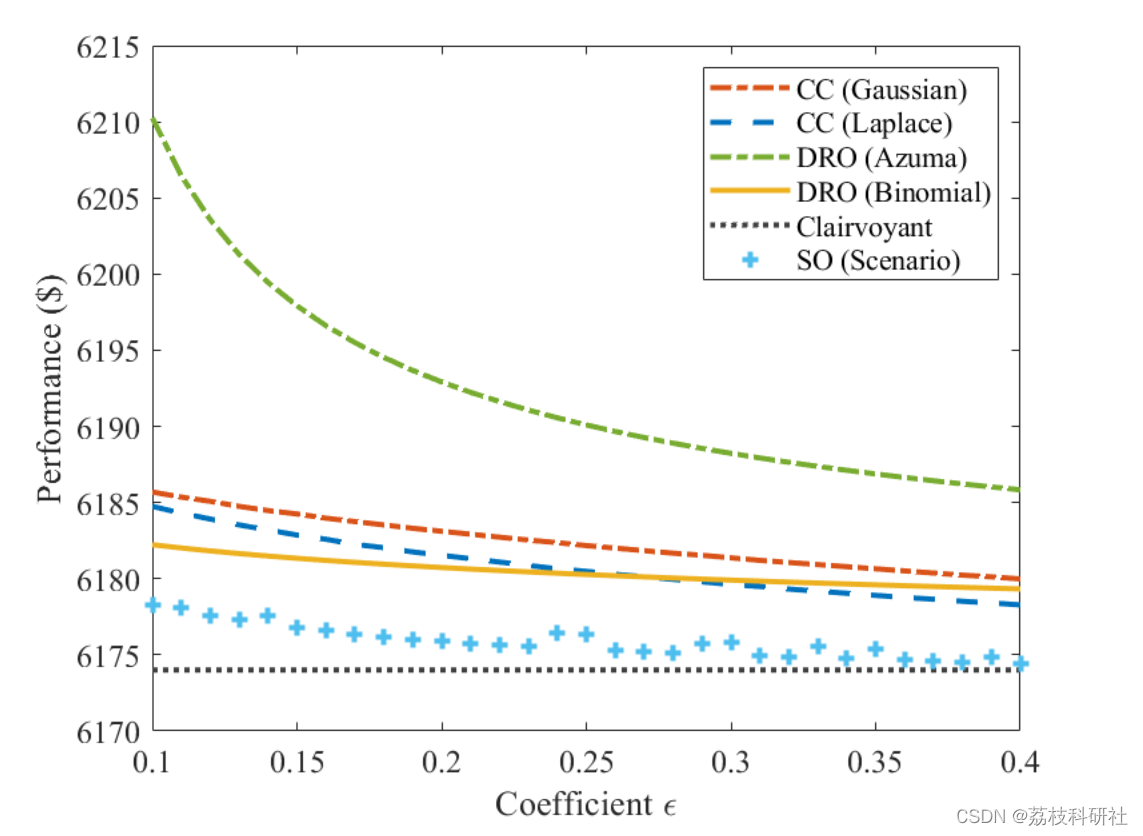
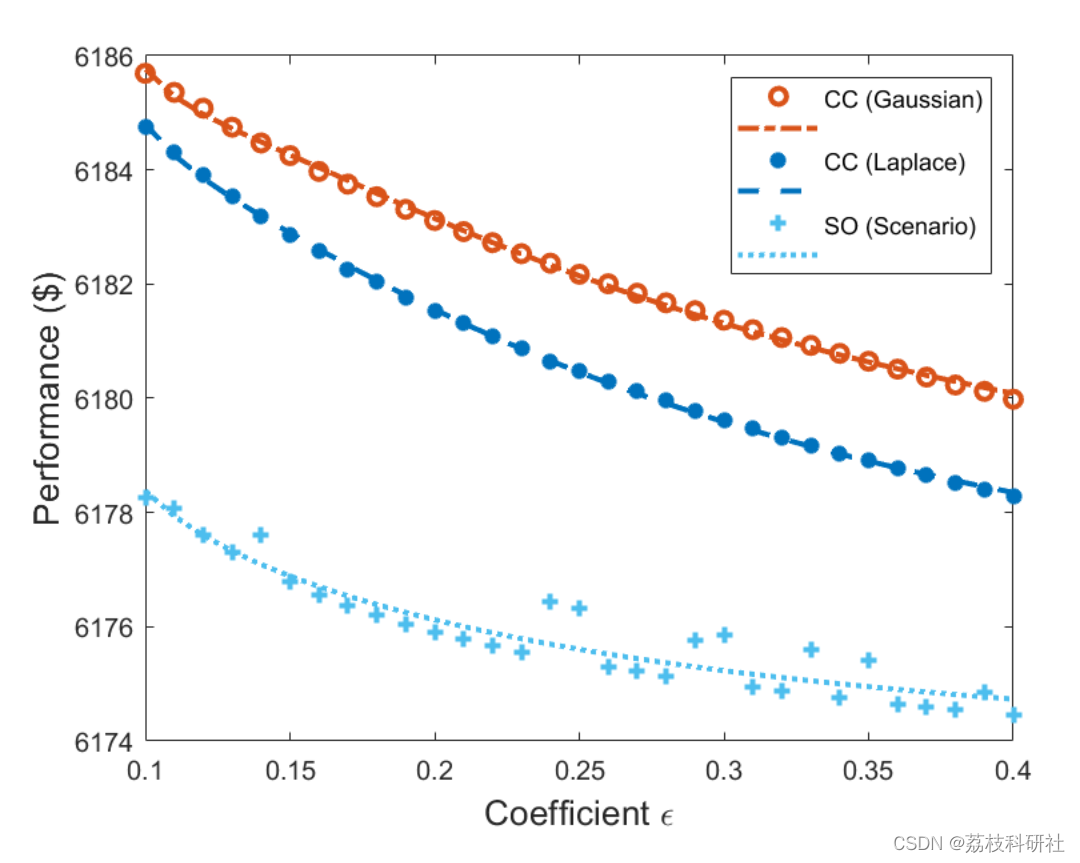
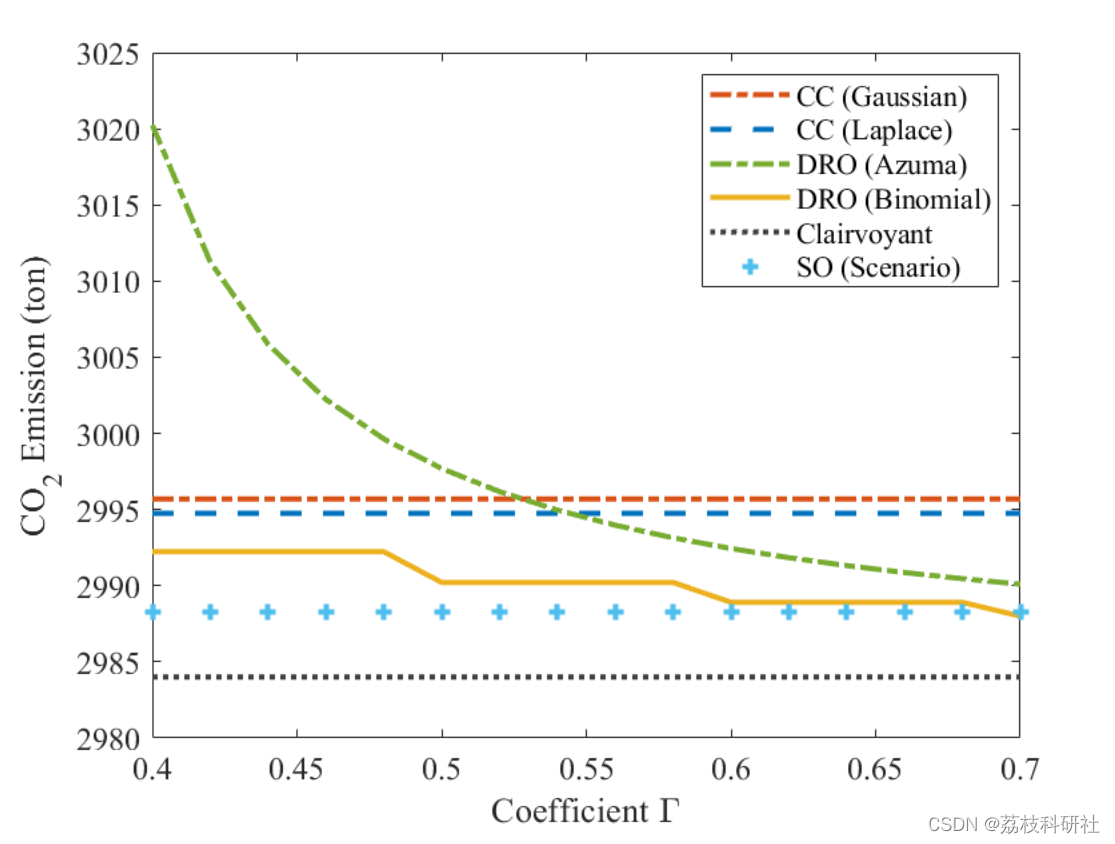
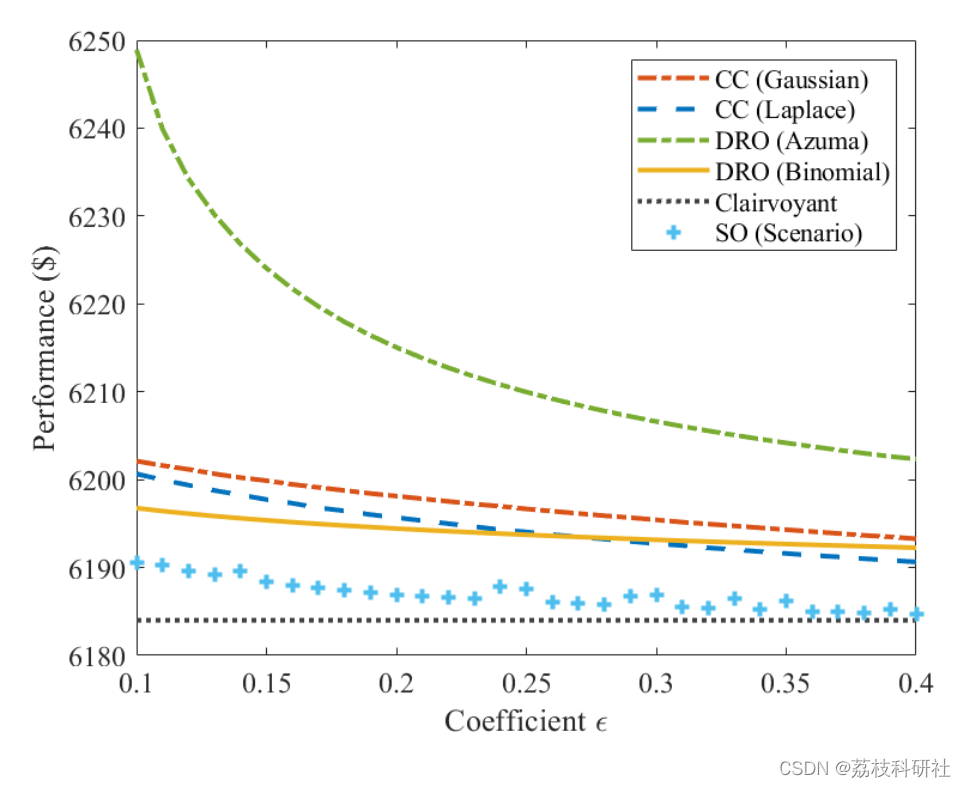
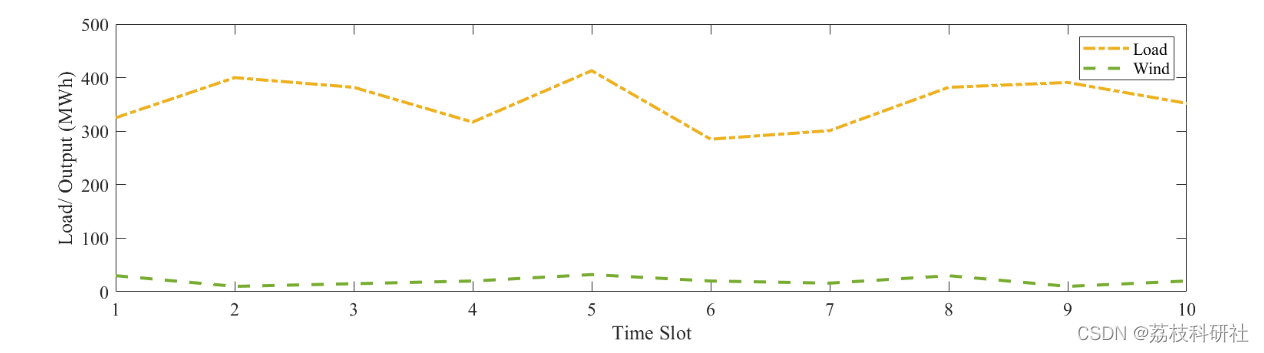
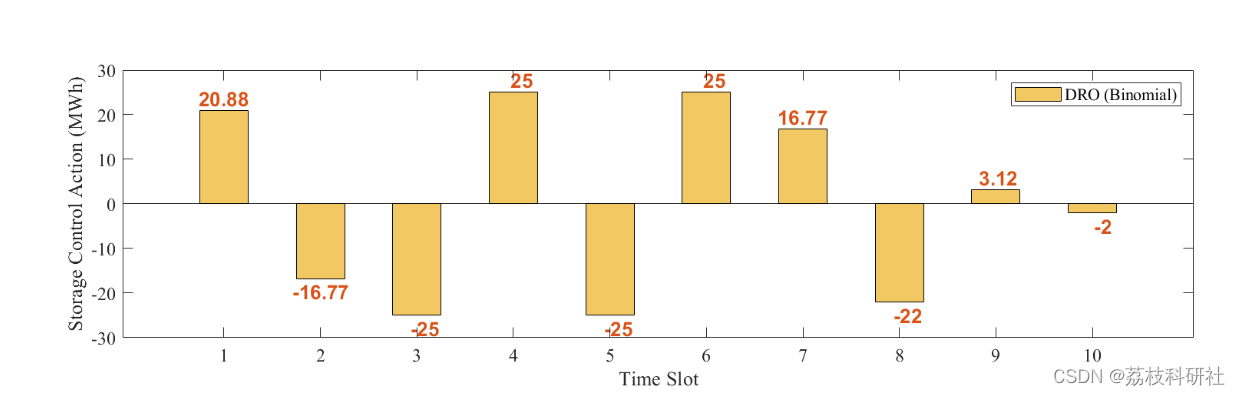
2.4 IEEE118

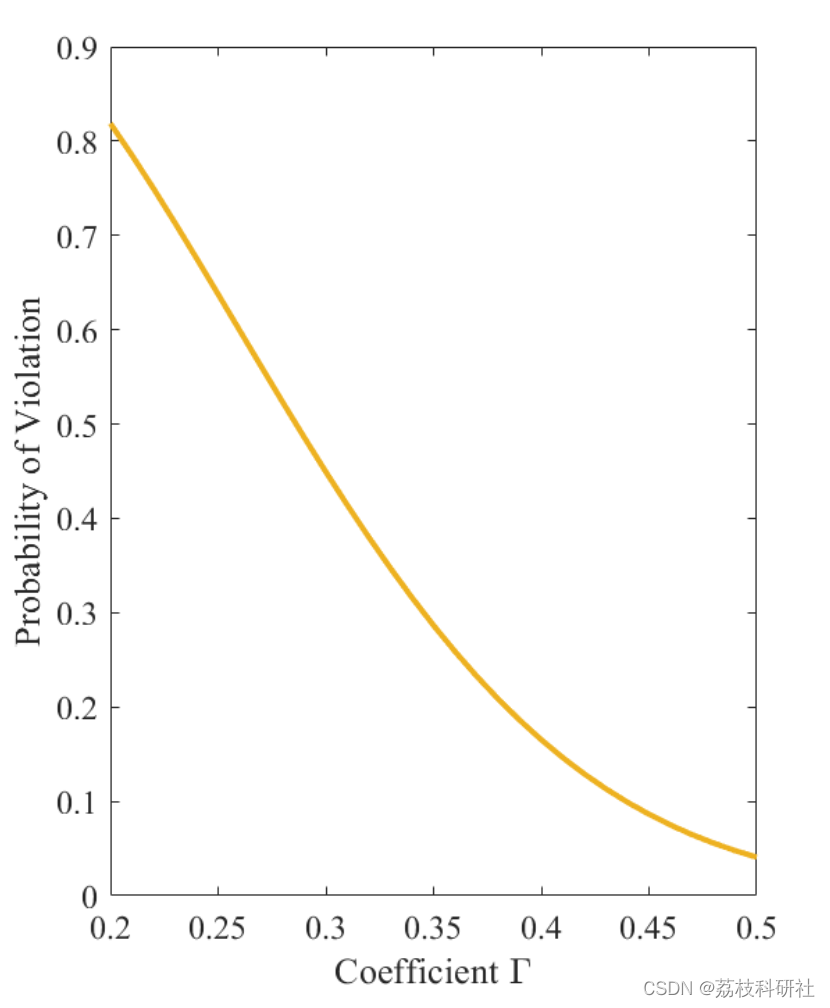
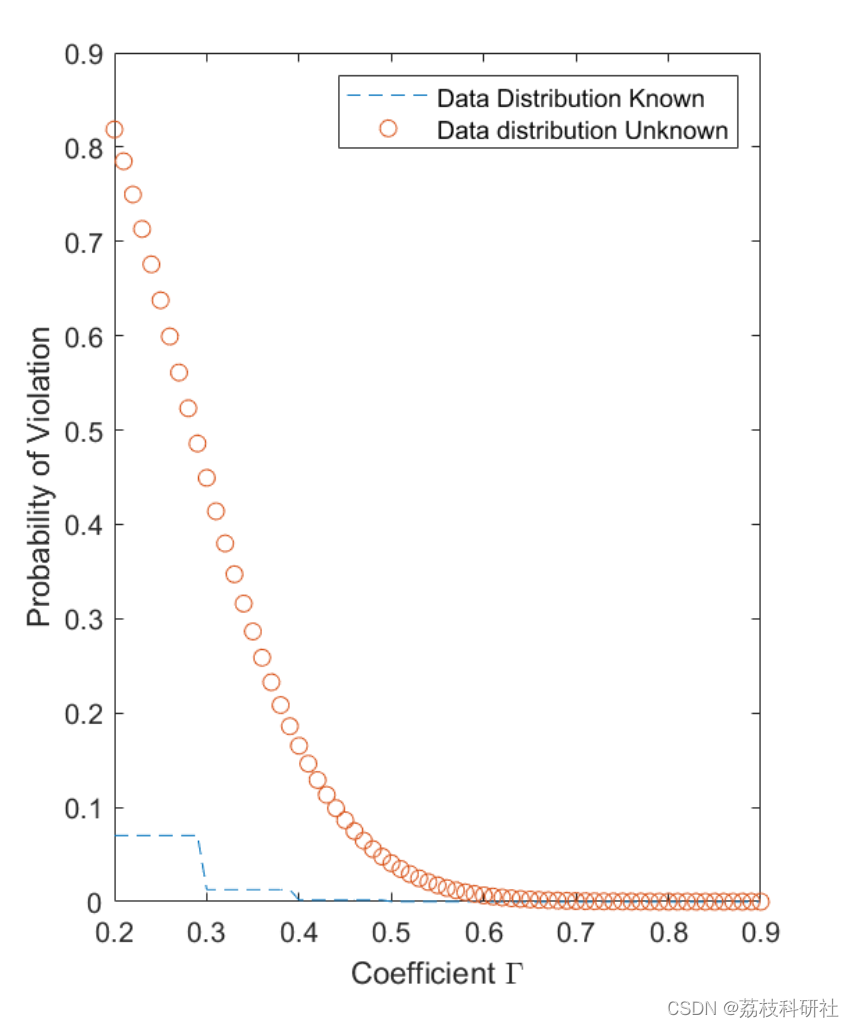
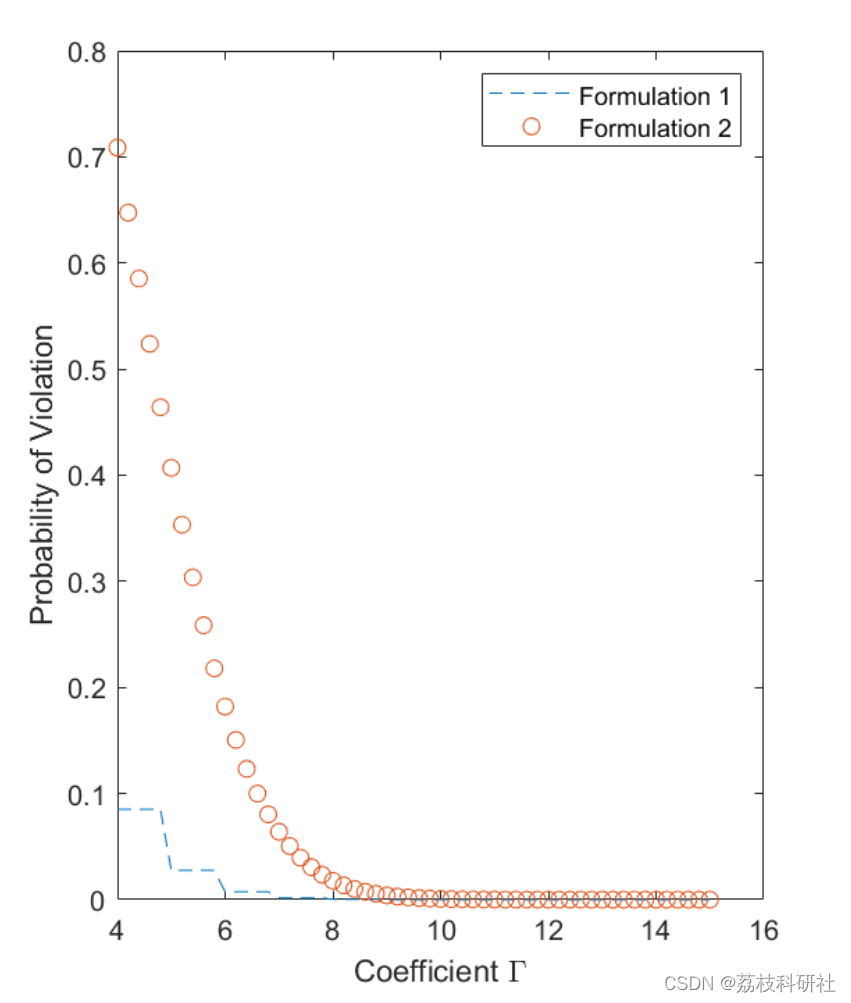
部分代码：

function[fval_avg,x_avg]=gen_SSO_average_performance(c_level,epsilon,T,N,M,bb,d_f,p,q,H,fmax,gmin,gmax,w_loc,w_num,error_data,ramp_rate,DR,UR)
% scenarios to be generated to meet the probability guarantee
n_dv=4*N*T;
Num=ceil(n_dv/(epsilon*c_level))-1;
% generating wind scenario
index=ceil(T*Num*(1-epsilon));
d_real=d_f;
virtual_bb=bb;

[gm] = gen_samples(error_data);

for k=1:w_num
loc=w_loc(k);
% random_num=zeros(T*Num,1);
% for i=1:Num
% rng('default');
% [random_T,~]=random(gm,T);
% random_num((i-1)*T+1:i*T)=random_T;
% end
rng('default');
random_num=random(gm,T*Num);
random_num=sort(random_num);
virtual_bb(loc)=max([bb(loc)-random_num(index),0]);
end

[standard_delta,real_bb]= gen_standard_delta(bb,virtual_bb,w_loc);

umin=-real_bb*ramp_rate;
umax=real_bb*ramp_rate;
[x_avg,fval_avg]=MinC(T,N,M,real_bb,d_real,p,q,H,fmax,gmin,gmax,umin,umax,DR,UR);
end

function[wind_error]= gen_wind_data(real_capacity_scale,filename)
%filename='.\data\WindGenTotalLoadYTD_2020.xls';
input_data= xlsread(filename, 1, 'B25:C52428');
input_scale=mean(input_data(:,1));
wind_data=input_data./input_scale*real_capacity_scale;
wind_error=wind_data(:,2)-wind_data(:,1);
% error_norm=normalize(error_data,'scale');
% wind_error=error_norm*ratio;
end