为什么会有退税和补税？

公司在帮我们进行个人所得税申报的时候，个人所得税是按月或者按季度预扣预缴的，税款会在每个月或季度的收入中扣除一定的比例。在年度个人所得税汇缴清算的时候，如果实际年度收入与预扣预缴的税款不符，就会出现补税或退税的情况。

补税举例

我们首先介绍一个最常见的补税的例子，就是换工作。为了方便计算，下面例子中提到的工资，全部以扣除五险一金和5000免征额之后的应纳税所得额来讲。

假设员工甲，在公司A工资为3W每月，5月份跳槽到了B公司，工资变成了4W每月。这时候，其在公司A已缴纳的个人所得税税额会被清零，简单理解为公司B在帮其缴纳个人所得税的时候，会认为员工甲今年从未交过税。

也就是说，他在公司A一共领到12W的薪水，公司B领到了32W的薪水，按照目前的计税方式，要缴纳的费用如下：

120000*10%-2520+320000*25%-31920=57560元

但是按照个人所得税税法，其应该缴纳的税款如下：

440000*0.3-52920=79080元

因此，员工甲就等于少缴纳了21520元的税，因此，个人所得税汇缴清算的时候，就需要补缴2.1W的税款，就出现了如下的场景：

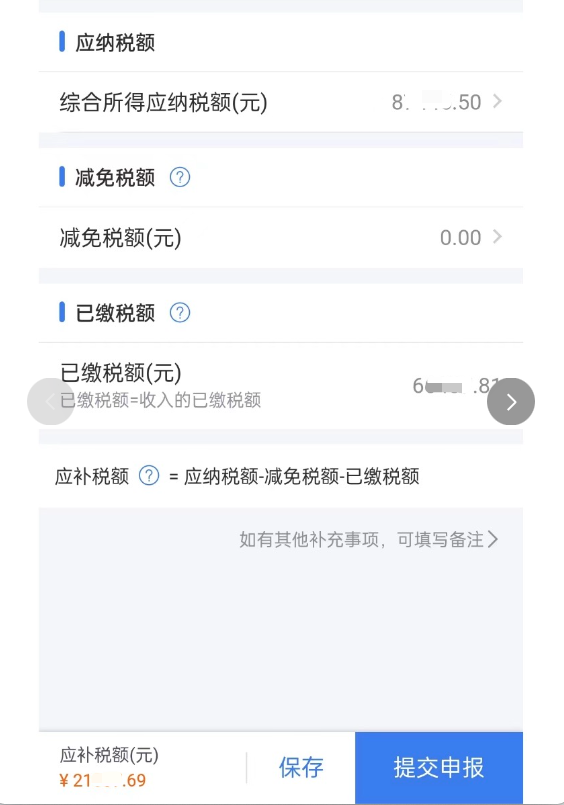
退税举例

接着我们再来介绍一个最常见的退税例子，个人所得税专项申报的抵扣，例子中提到的工资仍然以扣除五险一金和5000免征额之后的应纳税所得额来讲。

假设员工乙，在公司 C工资为2W每月，干了一整年，则其个人所得税应该缴纳：

240000*20%-16920=31080元。

但是员工乙这期间通过房贷买了房，这么就多了1.2W的抵扣额，其实际应该缴纳的个人所得税税额为：

(240000-12000)*20%-16920=28680元

所以，通过个人所得税汇缴申报，其应该获得2400元的退税额。

接下来，我们介绍一些合理合法的退税秘诀。

秘诀锦集

个人所得税专项抵扣，申报前一定要检查

个人所得税汇缴进行申报的时候，一定要检查一遍专项抵扣。换工作等原因，都会导致之前的申报失效。以及新的一年，或许就会有新的申报项目产生。因此，进行申报前，务必检查一遍专项抵扣的项目。专项抵扣的申请只要在个人所得税汇缴申报前完成即可。

除了下图中的7种项目之外，国家还新增了个人养老金专项抵扣，大家可以试试哦。

考一些专业资格证

上面有继续教育的选项，只要是国家认可的资格证，都是可以实现抵税的。

比如考证券从业资格证，基金从业资格证等等都是可以的，小编身边已经有好多朋友都考过了，反馈下来题目很简单，基本上都是单选题。

3600的抵扣额，按照30%的税率来算，就是1080块钱，但是报名需要61块钱，够小编吃一个月的大鸡腿了。

合理的选择奖金申报方式

如果在一年中领到过奖金，那么就会有一个奖金计税方式让你来选择，不同的选择方式，有可能就会导致你多缴税。

我们来举例说明：

假设员工甲，每个月的工资为5000块，专项抵扣额度为1.2W，年终奖1.2W。

方式1:选择单独计税，需要缴纳的税费为：(60000-60000-12000)*0%+12000*3%=360

方式2:选择并入综合所得计税，则需要缴纳的税费为：(60000+12000-60000-12000)*0%=0

则方式2可以节省360元的税费。

同样假设员工乙，每个月的工资为3W块，专项抵扣额度为1.2W，年终奖6W。

方式1:选择单独计税，需要缴纳的税费为：

(360000-60000-12000)*20%-16920+60000*10%=46680元。

方式2:选择并入综合所得计税，则需要缴纳的税费为：

(360000+60000-60000-12000)*25%-31920=55080

则方式1可以节省8400元的税费。

所以，如果全年累计工资不高并且专项抵扣额度较多，则建议选择全部并入综合所得的方式来计税，反之如果全年累积工资较高，则应该选择单独计税的方式。

一次性奖金要选择最大的那一笔

有的公司，一年之中会发多次奖金，也有可能有的人一年中换过公司领过多次奖金。一般来说公司的财务默认会帮申报第一次使用单独计税的名额。但是默认选择的这一笔并不一定最大的，因此要选择金额最大那一笔进行申报（这种方式适合年薪较高的）。

年个人所得税总额=年累计应纳税所得额*对应税率-速算扣除数+一次性奖金*对应税率

PS：奖金选择单独计税是没有速算扣除数的

举个例子，年薪40W，年终奖10W，如果选择年终奖单独计税，

则其应该缴纳的总税款为：400000*25%-31920+100000*10%=78080元。

个

人所得税税率表如下：

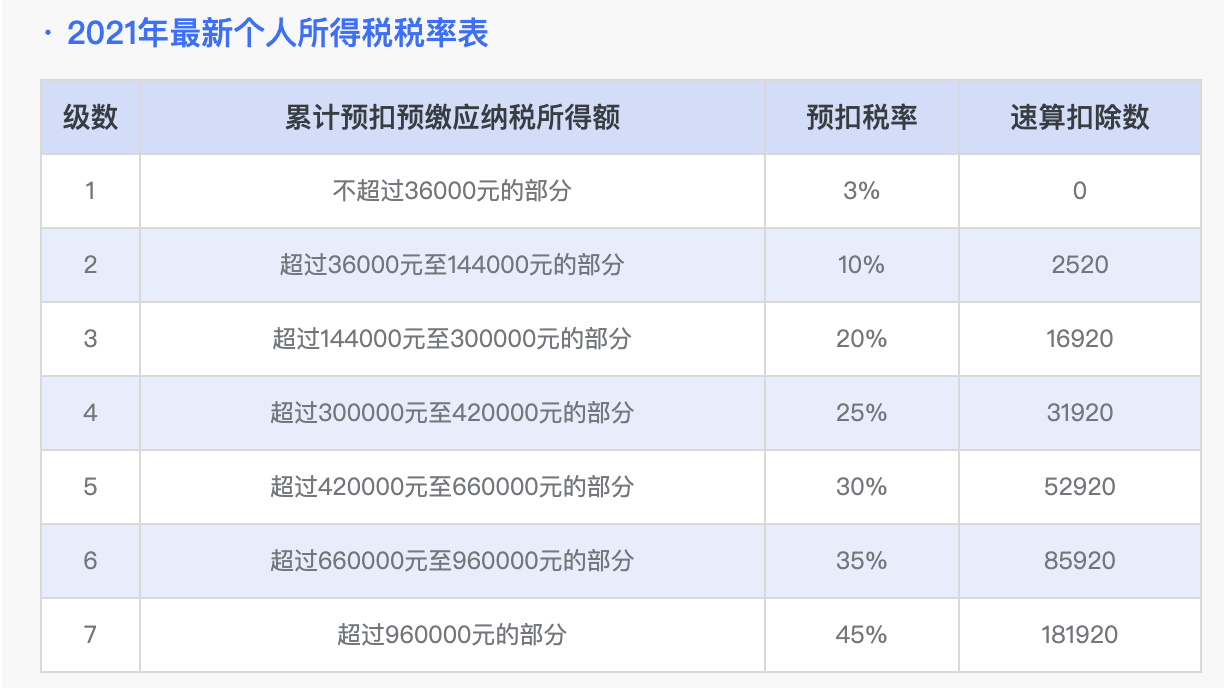
总结

本篇文章小编帮大家普及了一些所得税的只是，以及一些通过合理申报实现省税的秘诀，不知道大家学会了吗？如果读者们还有什么好的秘诀，也欢迎大家向小编建议哈。