机器学习算法: Logistic 回归详解

动动发财的小手，点个赞吧！

1. 导读

逻辑回归是在因变量为二元时进行的回归分析。它用于描述数据并解释一个因二元变量与一个或多个名义、有序、区间或比率水平变量之间的关系。
二元或二项式 Logistic 回归可以理解为处理其中因变量的观察结果只能是二元的场景的 Logistic 回归类型，即它只能有两种可能的类型。
多项 Logistic 回归适用于结果可能具有两种以上可能类型（A 型、B 型和 C 型）的情况，它们没有任何特定的顺序。

分类技术是机器学习和数据挖掘应用中的重要组成部分。解决分类问题的算法也有很多种，比如：k-近邻算法，使用距离计算来实现分类；决策树，通过构建直观易懂的树来实现分类；朴素贝叶斯，使用概率论构建分类器。这里我们要讲的是Logistic回归，它是一种很常见的用来解决二元分类问题的回归方法，它主要是通过寻找最优参数来正确地分类原始数据。

1. Logistic Regression

逻辑回归(Logistic Regression,简称LR)，其实是一个很有误导性的概念，虽然它的名字中带有“回归”两个字，但是它最擅长处理的却是分类问题。LR分类器适用于各项广义上的分类任务，例如：评论信息的正负情感分析（二分类）、用户点击率（二分类）、用户违约信息预测（二分类）、垃圾邮件检测（二分类）、疾病预测（二分类）、用户等级分类（多分类）等场景。我们这里主要讨论的是二分类问题。

2. 线性回归

逻辑回归和线性回归同属于广义线性模型，逻辑回归就是用线性回归模型的预测值去拟合真实标签的的对数几率（一个事件的几率（odds）是指该事件发生的概率与不发生的概率之比，如果该事件发生的概率是P，那么该事件的几率是

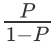
对数几率就是

逻辑回归和线性回归本质上都是得到一条直线，不同的是，线性回归的直线是尽可能去拟合输入变量X 的分布，使得训练集中所有样本点到直线的距离最短；而逻辑回归的直线是尽可能去拟合决策边界，使得训练集样本中的样本点尽可能分离开。因此，两者的目的是不同的。

线性回归方程：

此处，y为因变量，x为自变量。在机器学习中y是标签，x是特征。

3. Sigmoid 函数

在二分类的情况下，函数能输出0或1。拥有这类性质的函数称为海维赛德阶跃函数（Heaviside step function），又称之为单位阶跃函数（如下图所示）

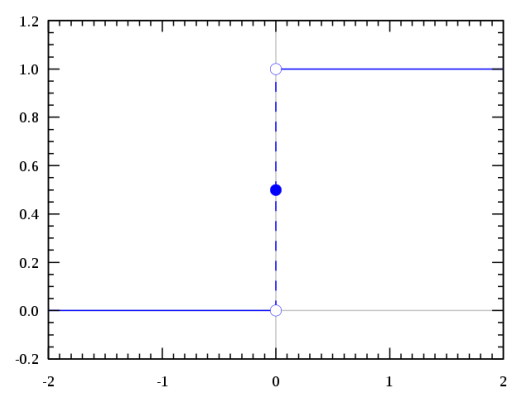
单位阶跃函数的问题在于：在0点位置该函数从0瞬间跳跃到1，这个瞬间跳跃过程很难处理（不好求导）。幸运的是，Sigmoid函数也有类似的性质，且数学上更容易处理。

Sigmoid函数公式：

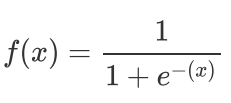
import numpy as np
import math
import matplotlib.pyplot as plt
%matplotlib inline

X = np.linspace(-5,5,200)
y = [1/(1+math.e**(-x)) for x in X]
plt.plot(X,y)
plt.show()

X = np.linspace(-60,60,200)
y = [1/(1+math.e**(-x)) for x in X]
plt.plot(X,y)
plt.show()

上图给出了Sigmoid函数在不同坐标尺度下的两条曲线。当x为0时，Sigmoid函数值为0.5。随着x的增大，对应的函数值将逼近于1；而随着x的减小，函数值逼近于0。所以Sigmoid函数值域为（0,1），注意这是开区间，它仅无限接近0和1。如果横坐标刻度足够大，Sigmoid函数看起来就很像一个阶跃函数了。

4. 逻辑回归

通过将线性模型和Sigmoid函数结合，我们可以得到逻辑回归的公式：

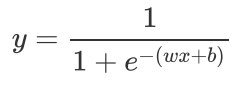
这样y就是（0,1）的取值。对式子进行变换，可得：

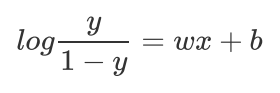
这个其实就是一个对数几率公式。

二项Logistic回归：

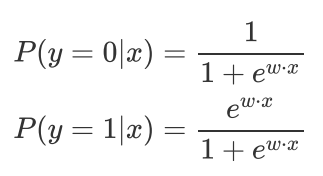
多项Logistic回归：

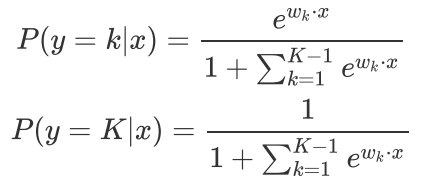
代码

import numpy as np

class LoisticRegression:
    # declaring learning rate and number of iterations(hyperparameters)
    def __init__(self, learning_rate=0.001, n_iters=1000):
        self.lr = learning_rate
        self.n_iters = n_iters
        self.weights = None
        self.bias = None
    
    def fit(self, X, y):
        n_samples, n_features = X.shape

        # initializing weights
        self.weights = np.zeros(n_features)  

        # initializing bias
        self.bias = 0

        # Gradient descent
        for i in range(self.n_iters):

            # applying the linear model
            linear_model = np.dot(X, self.weights) + self.bias

            # defining the predict method
            y_predicted = self._sigmoid(linear_model)

            # compute the gradients
            dw = (1 / n_samples) * np.dot(X.T, (y_predicted - y))
            db = (1 / n_samples) * np.sum(y_predicted - y)

            # update the parameters
            self.weights -= self.lr * dw
            self.bias -= self.lr * db

    # get the test samples that we want to predict
    def predict(self, X):
        # applying the linear model
        linear_model = np.dot(X, self.weights) + self.bias

        # defining the predict method
        y_predicted = self._sigmoid(linear_model)
        y_predicted_cls = [1 if i > 0.5 else 0 for i in y_predicted]
        return np.array(y_predicted_cls)

    def _sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

5. LR 与线性回归的区别

逻辑回归和线性回归是两类模型，逻辑回归是分类模型，线性回归是回归模型。

6. LR 损失函数

损失函数，通俗讲，就是衡量真实值和预测值之间差距的函数。所以，损失函数越小,模型就越好。在这里，最小损失是0。

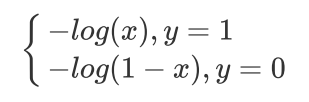
# 函数的图像
X = np.linspace(0.0001,1,200)
y = [(-np.log(x)) for x in X]
plt.plot(X,y)
plt.show()

X = np.linspace(0,0.99999,200)
y = [(-np.log(1-x)) for x in X]
plt.plot(X,y)
plt.show()

把这两个损失函数综合起来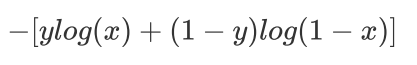： alt

y就是标签，分别取0，1。

对于m个样本，总的损失函数为：

这个式子中，m是样本数，y是标签，取值0或1，i表示第i个样本，p(x)表示预测的输出。

7. 实例

使用Logistic回归来预测患疝气病的马的存活问题。原始数据集下载地址^[1]

数据包含了368个样本和28个特征。该数据集中包含了医院检测马疝病的一些指标，有的指标比较主观，有的指标难以测量，例如马的疼痛级别。另外需要说明的是，除了部分指标主观和难以测量外，该数据还存在一个问题，数据集中有30%的值是缺失的。下面将首先介绍如何处理数据集中的数据缺失问题，然后再利用Logistic回归和随机梯度上升算法来预测病马的生死。

7.1. 数据准备

数据中的缺失值解决办法：

使用可用特征的均值来填补缺失值；
使用特殊值来填补缺失值，如-1；
忽略有缺失值的样本；
使用相似样本的均值添补缺失值；
使用另外的机器学习算法预测缺失值。

预处理数据做两件事：

如果测试集中一条数据的 特征值已经缺失，那么我们选择实数0来替换所有缺失值，因为本文使用 Logistic回归。因此这样做不会影响回归系数的值。sigmoid(0)=0.5，即它对结果的预测不具有任何倾向性。
如果测试集中一条数据的 类别标签已经缺失，那么我们将该类别数据丢弃，因为类别标签与特征不同，很难确定采用某个合适的值来替换。

train = pd.read_table('horseColicTraining.txt',header=None)
train.head()
train.shape
train.info()

test = pd.read_table('horseColicTest.txt',header=None)
test.head()
test.shape
test.info()

7.2. 回归

得到训练集和测试集之后，可以得到训练集的weights。这里需要定义一个分类函数，根据sigmoid函数返回的值来确定y是0还是1。

"""
函数功能：给定测试数据和权重，返回标签类别
参数说明：
    inX：测试数据
    weights：特征权重
"""

def classify(inX,weights):
    p = sigmoid(sum(inX * weights))
    if p < 0.5:
     return 0
    else:
     return 1

7.3. 模型构建

"""
函数功能：logistic分类模型
参数说明：
    train：测试集
    test：训练集
    alpha：步长
    maxCycles：最大迭代次数
返回：
 retest:预测好标签的测试集
"""

def get_acc(train,test,alpha=0.001, maxCycles=5000):
    weights = SGD_LR(train,alpha=alpha,maxCycles=maxCycles)
    xMat = np.mat(test.iloc[:, :-1].values)
    xMat = regularize(xMat)
    result = []
    
    for inX in xMat:
        label = classify(inX,weights)
        result.append(label)
    retest=test.copy()
    retest['predict']=result
    acc = (retest.iloc[:,-1]==retest.iloc[:,-2]).mean()
    
    print(f'模型准确率为：{acc}')
    
    return retest

运行结果

get_acc(train,test,alpha=0.001, maxCycles=5000)

运行10次查看结果：

for i in range(10):
 acc =get_acc(train,test,alpha=0.001, maxCycles=5000)

从结果看出，模型预测的准确率基本维持在74%左右，原因有两点：

数据集本身有缺失值，处理之后对结果也会有影响；
逻辑回归这个算法本身也有上限。

参考资料

[1]

dataset: http://archive.ics.uci.edu/ml/datasets/Horse+Colic

本文由 mdnice 多平台发布