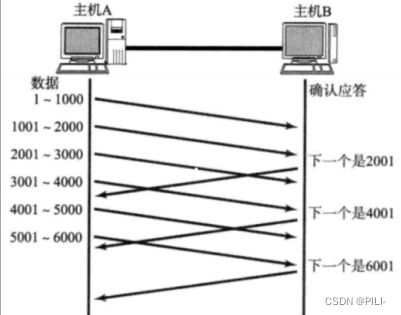
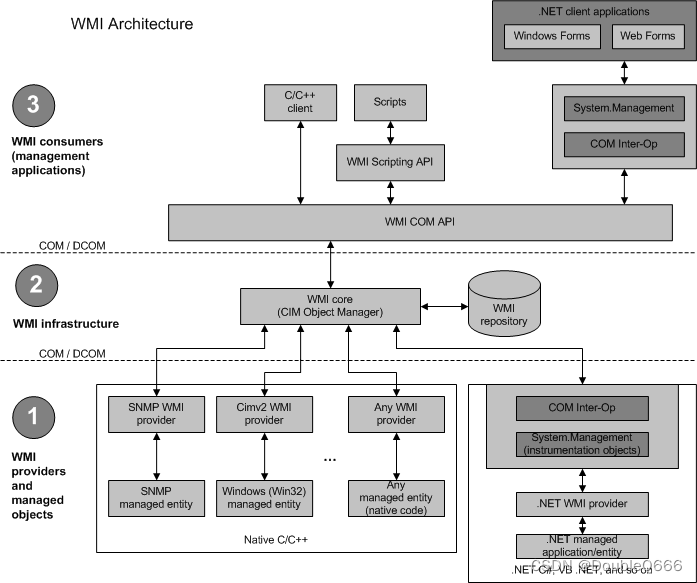
论文阅读：Syntax-Aware Network for Handwritten Mathematical Expression Recognition¹

主要观点：

1、提出将语法信息纳入编码器-解码器网络的方法。使用一组语法规则，用于将每个表达式的LaTeX标记序列转换为解析树；用深度神经网络将标记序列预测建模为树遍历过程。

2、该方法可以有效地描述表达式的语法上下文，减小HMER的结构预测误差。和现有的WAP和WAP-TD相比，考虑语法规则。

Figure 1. Comparison of different architectures: (a) An encoder-decoder framework WAP (b) A tree decoder DWAP-TD © Our model Syntax-Aware Network (SAN)

相关工作：

HMER的主要任务：

• 对同一符号的笔画进行切分；
• 符号识别；
• 语法引导下的符号结构关系分析，生成数学表达式；

HMER的难点不在于符号识别，而是符号的语法关系；

序列法：

• 首先将表达式分段输入数学符号，对每个符号分别进行分类，然后通过结构关系分析识别数学表达式。这些方法采用了分类技术，如HMM，弹性匹配，支持向量机、和树变换。

• 全局方法应用一种综合策略来学习数学符号及其结构关系分析，同时隐式地分割符号。这些方法将HMER处理为基于符号识别结果的数学表达式分割、符号识别和表达式识别结构的全局优化

深度学习方法：

• 序列到序列：转换数学表达式图片到标记序列，加注意力机制等；

• 图到图的方法：探索输入公式的结构关系到标记序列；

• 树结构方法：尝试使用树结构的解码器，对图片提取的特征进行解码；

算法原理：

基本规则

1)遵循标准的阅读顺序:从左到右，从上到下。

2)利用相邻符号之间的空间关系。对于一对相邻的HME符号，总共有九种可能的关系(左、右、上、下、左下、右下、左上、右上、内)。由于约束1)，我们去掉了“左”和“下左”，保留了其余7种关系来处理我们实现中所有的MEs情况。尽管ME可能对应于不同的LaTeX序列，但由于这两个约束，语法规则生成的语法树是相同的。

数学描述

算法由元组表示：
$$G=(N,\Sigma ,R,S,\Gamma ,C,D),$$
$N$：非终止符，包括起始符$S$和拓展符$E$；

$\Sigma$：终止符；

$R$：产生式规则；

$\Gamma$：关系；

$C$：编码器；

$D$：解码器；

产生式规则

产生式规则可以表示成：
$$\begin{gathered} \alpha \to \beta , \\ \alpha \in N,\beta \in (\Gamma \cup N\cup \Sigma {)}^{\ast }. \end{gathered}$$
asterisk: represents the Kleene star operation²

$R$有两条生成规则：

规则1：$S$可以在后面产生任意的终止符；或者$E$扩展符；或者空字符$ϵ$
$$S\to \sigma S|E|ϵ,$$
$\sigma$：$\sigma \in \Sigma$；

$|$：任选的意思；

规则2：$E$为每种类型的关系产生字符串，然后拼接起来；字符串后面可以跟$S$或者空字符串；
$$E\to [(({\gamma }_1)S|ϵ),\dots ,(({\gamma }_7)S|ϵ)],$$
${\gamma }_i\in \Gamma$：在关系中的第$i$种；

表达规则图示

图3示出了具有产生式规则的表达式的可能解析过程。为了直观地理解这些规则，可以把S看成一个表达式，把E看成一个可扩展的结构。假设一个表达式可以包含多个可扩展结构，而每个可扩展结构可以扩展为多个具有空间关系的表达式。此外，产生式规则与以输入图像和父节点的上下文状态为条件的概率相关。具体来说，条件概率定义为：
$$p(\alpha \to \beta |c(\alpha ),X)=D_{\alpha \to \beta }(c(\alpha ),E(X)),$$
$X$:输入图像；

$E(X)$：编码器的输出；

$c(\alpha )$是$\alpha$的上下文状态(将在第3.2节中详细介绍)，$D\alpha \to \beta (\cdot )$是对应于产生式规则的解码器的输出；

Figure 3. (a) A possible parsing procedure of ${\sum }_i^{n}a$ and (b) the parse tree. In the figure, the strings refer to non-terminal symbols in blue, terminal symbols in red, relations in yellow, and empty in grey.

基本流程

如算法1所示，给定SAN参数和输入图像，使用堆栈实现树遍历。具体来说，所实现的栈可以保证训练过程按照语法树的遍历顺序进行。同样，预测过程也是通过逐步堆叠来实现的。编码器获取输入图像并对其进行下采样。然后根据语法规则，确定表达式及其可扩展结构;同时，解码器计算并选择概率最高的产生式规则。因此，生成具有可扩展结构的新表达式，并更新LaTeX序列中图像的解析树。一旦找到解析树，就可以通过预先顺序遍历树来获得识别结果。

符号感知解码器

Figure 4. Syntax-Aware Decoder: Consisting of GRU-α, GRU-β, and the Syntax-Aware Attention Module

损失函数：
$$\mathcal{L}={\mathcal{L}}_{symbol}+{\mathcal{L}}_{relation}+{\mathcal{L}}_{symbol}^{rev}+{\mathcal{L}}_{reg}.$$

实验结论：

评价方法：

表达式识别率(ExpRate)是数学表达式识别中广泛使用的一种识别协议，定义为预测的数学表达式准确匹配标准答案的百分比。ExpRate≤1和≤2表示表达式识别率最多可容忍一个或两个符号级错误。

在公开数据集CROHME上：

在HME100k上：

参考：

---

1. [2203.01601] Syntax-Aware Network for Handwritten Mathematical Expression Recognition (arxiv.org) ↩︎

2. Kleene星号_百度百科 (baidu.com) ↩︎