交并比（IOU）的计算方法

news2025/1/22 19:51:19

交并比（IOU, Intersetion Over Union）,意思就是交集和并集的比值，用来评价两个几何图形的面积重合度，在目标检测算法模型中，通常被用来计算预测框与真实框的误差（损失函数）或者在非极大值抑制（NMS）算法中用于过滤多余重叠的目标，亦或者在计算mAP时用于判断目标是否被预测到。这是一个应用非常广泛的算法，这里详细介绍一下它的算法原理，以及代码的实现方式。

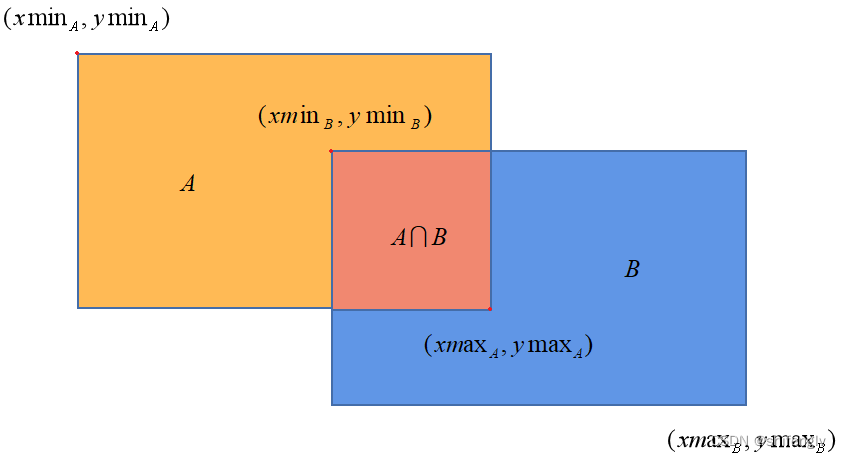
如图1所示的是两个矩形方框的交并比示意图，中间重合部分就是矩形A和矩形B的交集，那么这两个矩形框的交并比计算公式如下：

$IOU=\frac{A\cap B}{A\cup B}$

其中，A与B的并集又可以通过以下公式计算：

$A\cup B=A+B-A\cap B$

定义矩形 A和矩形B的对角坐标分别为 $[\left ( xmin_{A},ymin_{A} \right ),\left ( xmax_{A},ymax_{A} \right )]$ 、 $[\left ( xmin_{B},ymin_{B} \right ),\left ( xmax_{B},ymax_{B} \right )]$ ，同时又定义交集矩形的对角坐标为 $[\left ( xmin_{AB},ymin_{AB} \right ),\left ( xmax_{AB},ymax_{AB} \right )]$ ，那么交集矩形对角坐标的计算方法如下：

$xmin_{AB}=max(xmin_{A},xmin_{B})$

$ymin_{AB}=max(ymin_{A},ymin_{B})$

$xmax_{AB}=min(xmax_{A},xmax_{B})$

$ymax_{AB}=min(ymax_{A},ymax_{B})$

于是，交集和并集的计算如下：

$A\cap B=\left ( xmax_{AB}-xmin_{AB} \right )*\left ( ymax_{AB} -ymin_{AB}\right )$

$W_{A}=xmax_{A}-xmin_{A}$

$H_{A}=ymax_{A}-ymin_{A}$

$W_{B}=xmax_{B}-xmin_{B}$

$H_{B}=xmax_{B}-xmin_{B}$

$A\cup B=W_{A}*H_{A}+W_{B}*H_{B}-A\cap B$

以上公式，是根据两个矩形有交集的情况推导出来的，如果两个矩形没有交集，以上公式如何做出判断呢？如果是这两个矩形不存在交集，那么只要判断 $A\cap B\leq 0$ 即可，即是说，如果两个矩形无交集，那么交并比为0。以下分别以python和C语言代码实现交并比的计算。

python代码实现如下：

def iou(b1,b2):
    xmin1,ymin1,xmax1,ymax1=b1
    xmin2,ymin2,xmax2,ymax2=b2
    w1=xmax1-xmin1
    h1=ymax1-ymin1
    w2=xmax2-xmin2
    h2=ymax2-ymin2
    xmin_inter=max(xmin1,xmin2)
    ymin_inter=max(ymin1,ymin2)
    xmax_inter=min(xmax1,xmax2)
    ymax_inter=min(ymax1,ymax2)
    inter=(xmax_inter-xmin_inter)*(ymax_inter-ymin_inter)
    union=w1*h1+w2*h2-inter
    if inter<=0:
        return 0
    else:
        return inter/union

C语言代码实现如下：

struct Box
{
	double xmin;
	double ymin;
	double xmax;
	double ymax;
};

double iou(Box b1, Box b2)
{
	double w1 = b1.xmax - b1.xmin;
	double h1 = b1.ymax - b1.ymin;
	double w2 = b2.xmax - b2.xmin;
	double h2 = b2.ymax - b2.ymin;
	double xmin_inter,ymin_inter,xmax_inter,ymax_inter;
	xmin_inter = (b1.xmin > b2.xmin) ? b1.xmin : b2.xmin;
	ymin_inter = (b1.ymin > b2.ymin) ? b1.ymin : b2.ymin;
	xmax_inter = (b1.xmax < b2.xmax) ? b1.xmax : b2.xmax;
	ymax_inter = (b1.ymax < b2.ymax) ? b1.ymax : b2.ymax;
	double inter=(xmax_inter-xmin_inter)*(ymax_inter-ymin_inter);
	double un=w1*h1+w2*h2-inter;
	if(inter<=0)return 0;
	else return inter/un;
}