一、简介

1.博主这里使用的是腾讯云的服务，然后使用Docker进行部署Remix。

2.踩了几个坑，没有花费过多时间，所以这篇文章会记录踩过的坑。然后避免你们掉进去，然后花费过多时间。

3.这里就不写怎么安装Docker了，因为博主上篇文章已经写了，请看博主编写的Ubuntu安装Docker那篇文章。这里就写怎么进行部署的。https://blog.csdn.net/m0_58724783/article/details/129391863?spm=1001.2014.3001.5501

二、部署简要：

1.要基本会使用Linux，因为Ubuntu是基于linux内核的一个发行版；

2.不会使用Docker无关紧要，需要懂得一些网络的原理，这样稍微遇到问题可以快速进行定位，不用过多的去花费时间。

3.必须要提前安装好了Docker，不然直接操作不行的。

4.好了，接下来是实操了。

三、实操部署

1.使用Docker拉取Remix镜像，使用以下命令：

sudo docker pull remixproject/remix-ide

2.拉取成功，然后使用Docker启动Remix镜像，使用以下命令：

sudo docker run -p 8080:80 remixproject/remix-ide

注：这里有个坑，不要使用 docker run -p 8080:8080启动，因为80端口是docker的，8080是Remix的，但是8080在docker里面是没有的，但是也能启动的起来，但是使用telnet或者curl进行测试的时候是有问题的，映射的端口有问题，所以会导致连接被拒绝或者其他问题；这个是博主在排查问题的时候，在docker文件中看见了，踩到了这个坑。

3.开放端口对外

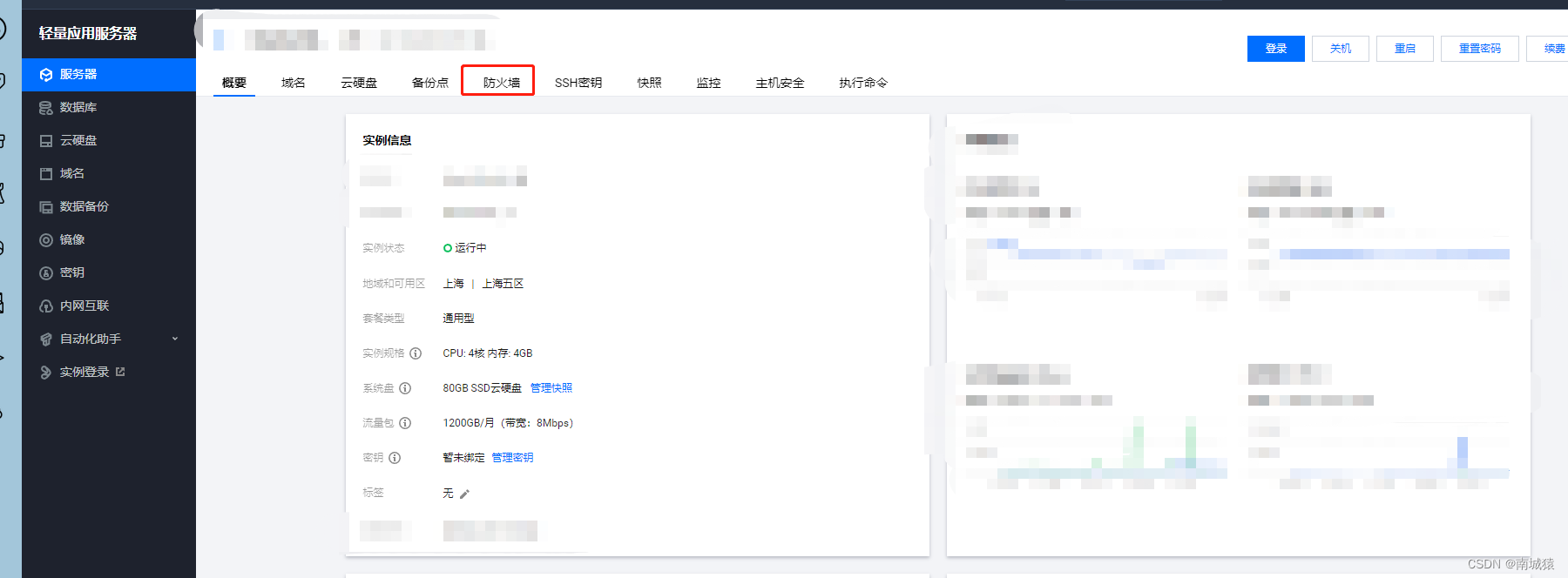
3.1.前面也说了，博主使用的是腾讯云的，所以有可能跟你们不一样。

3.2.进入到你的实列详情里面，然后点击防火墙，然后添加规则，跟博主一样就可以了。

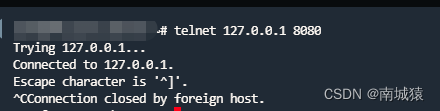
4.可以使用telnet/curl 进行测试，如下：

注：这样是通了，但是要是不是这样，在看一下配置是哪里的问题，或者可以来这里交流，我看见了会回复的。

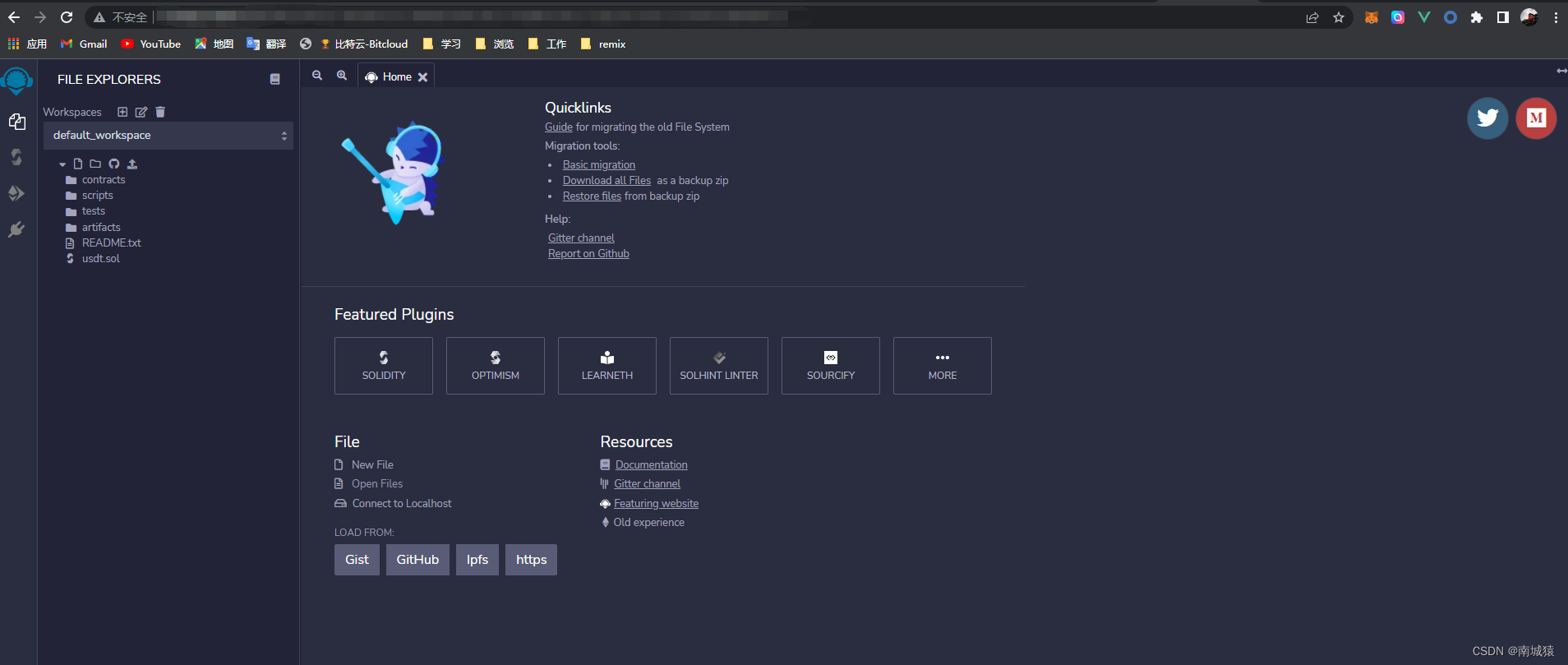
5.把你的腾讯云的公网IP，然后加上端口，输入到浏览器上，就可以访问了。

.有可能加载的会比较慢，因为它要下载文件，所以会比较慢。

注：使用终端需要两个，不要使用一个，也可以一个，把docker放在后台进行运行，

敲命令的时候run -p -d image_name 就可以了。

四、到这里就可以成功的部署好了，加油！